52.N皇后Ⅱ python

题目

题目描述

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

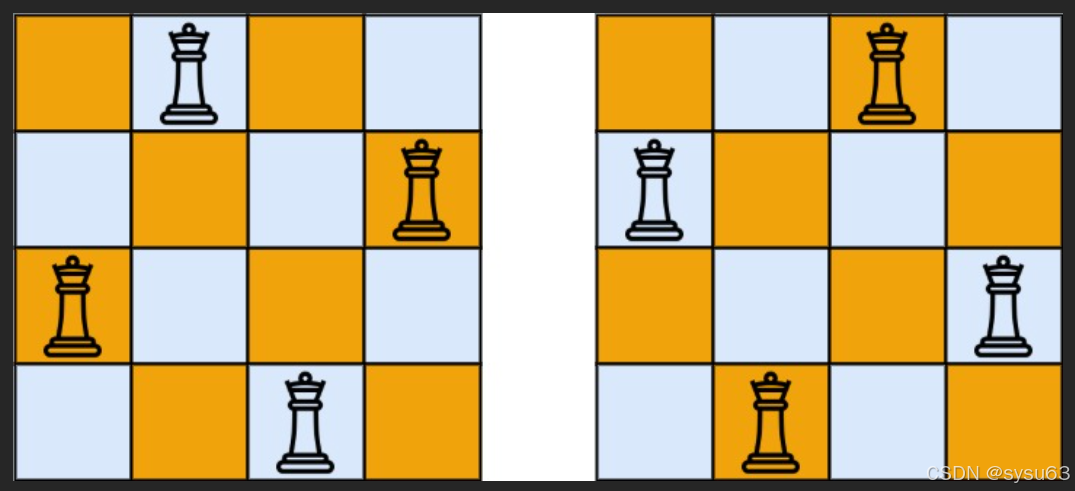
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 9

题解

为了解决这个问题，我们可以采用回溯算法。与求解所有n皇后问题的解决方案类似，这里的目标是计算有多少种不同的方法可以放置皇后，而不是实际生成这些布局。因此，我们可以简化原始的n皇后求解算法，只关注于计数。

算法思路

1. 初始化：定义一个计数器count来记录有效配置的数量。
2. 递归函数：创建一个递归函数来尝试在每一行中放置一个皇后，并检查该位置是否会导致冲突。
3. 基础情况：当行索引等于n时，说明已经成功放置了n个皇后，此时增加计数器count。
4. 尝试放置皇后：对于当前行的每一列，尝试放置一个皇后。
5. 检查冲突：编写一个辅助函数来检查新位置是否与已放置的皇后冲突（同一列或对角线）。
6. 回溯：如果当前位置不冲突，则继续下一行；否则，回溯并尝试下一列。
7. 返回结果：最终返回计数器count的值。

下面是Python代码实现：

def totalNQueens(n):
    def could_place(row, col):
        # 检查是否可以在第row行第col列放置皇后