51.N皇后 python

题目

题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

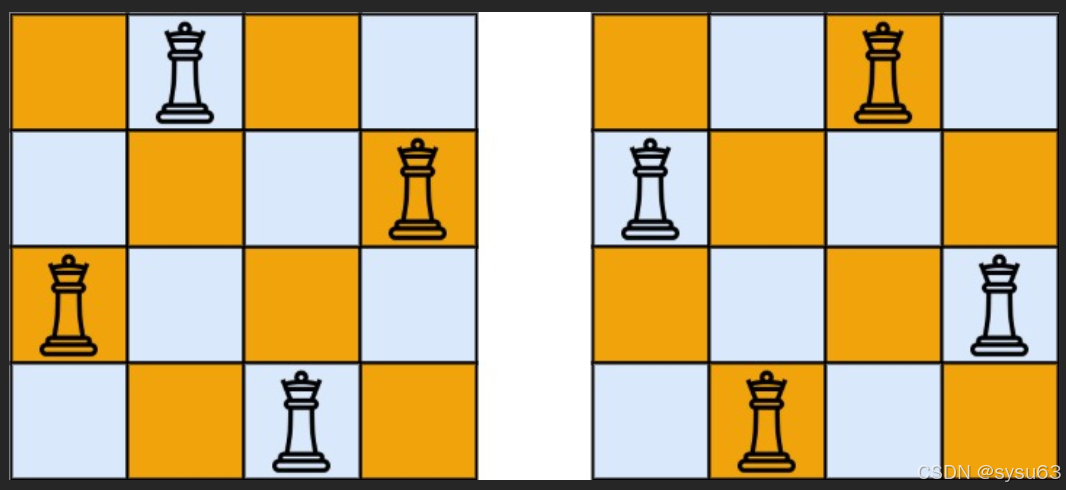
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[[“Q”]]

提示：

1 <= n <= 9

题解

解决n皇后问题的经典方法是使用回溯算法。回溯是一种通过构建所有可能的候选解并尽可能早地放弃那些不可能成功的候选解来解决问题的技术。对于n皇后问题，这意味着尝试在棋盘上的每一行放置一个皇后，并检查该位置是否会导致冲突（即两个皇后在同一列或同一对角线上）。如果当前位置不会导致冲突，则继续下一行；否则，回退并尝试另一个位置。

算法步骤

1. 初始化：创建一个空的结果列表用于存储所有的解，以及一个当前解的表示（可以是一个字符串列表，每个字符串代表棋盘的一行）。
2. 递归函数：定义一个递归函数，该函数接收当前处理的行索引作为参数。
3. 基础情况：当行索引等于n时，说明已经成功放置了n个皇后，此时将当前解加入到结果列表中。
4. 尝试放置皇后：对于当前行的每一列，尝试放置一个皇后。
5. 检查冲突：编写一个辅助函数来检查新位置是否与已放置的皇后冲突。
6. 回溯：如果当前位置不冲突，则递归调用处理下一行。如果发生冲突或者到达叶子节点后没有找到解，则移除最后一个皇后（回溯），然后尝试下一列。
7. 返回结果：当所有可能性都被探索完毕后，返回结果列表。

下面是Python代码实现：

def solveNQueens(n):
    def could_place(row, col):
        # 检查是否可以在第row行第col列放置皇后
        return not (cols