本文介绍了图论中的最短路径问题，包括四种主流算法：Floyd-Warshall、Dijkstra、Bellman-Ford（SPFA）和Johnson，以及A*算法。Floyd算法适用于加权图的多源最短路径，Dijkstra算法用于计算单源最短路径，但不支持负权边；Bellman-Ford算法能处理负权边，但时间复杂度较高；SPFA是Bellman-Ford的优化；Johnson算法则能处理带负权重的图；A*算法是静态路网中求解最短路径的有效搜索方法。
目录：
最短路径简介：
最短路径问题是图论研究中的一个经典算法问题， 旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。 算法具体的形式包括：
(1)确定起点的最短路径问题（ 即已知起始结点），求最短路径的问题。
(2)确定终点的最短路径问题（与确定起点的问题相反），该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
(3)确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
(4)全局最短路径问题 - 求图中所有的最短路径。
解决最短路径问题有 5 种主流的算法：Floyd算法 \ Floyd-warshall算法，Dijkstra算法，Bellman-Ford算法 \ SPFA算法，Johnson算法，A*算法。
Floyd算法 \ Floyd-warshall算法：
Floyd算法 和 Floyd-warshall算法 实际上是一个东西，只不过是名字不同罢了。
Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授 罗伯特·弗洛伊德 命名。
Floyd算法的边权值可正可负，但需要使用邻接矩阵存储图的边权值。
时间复杂度：O()
【代码实现】
//假设有n个点，m条边，求1~n的最短路径
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m;
int mapp[1001][1001];
int clean()//初始化
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j)
{
mapp[i][j]=0;
}
else
{
mapp[i][j]=0x7f7f7f;
//mapp[i][j]=- 0x7f7f7f;
//初始为无穷大或无穷小，需要根据题目变通
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);//读入
clead();//初始化
for(int i=1;i<=m;i++)//读入边的值
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
mapp[u][v]=w;//有向图
//mapp[u][v]=mapp[v][u]=w;无向图
}
for(int k=1;k<=n;k++)//Floyd算法模板
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(mapp[i][k]+mapp[k][j]<mapp[i][j])
{
mapp[i][j]=mapp[i][k]+mapp[k][j];
}
}
}
}
printf("%d\n",mapp[1][n]);//输出
return 0;
}Dijkstra算法：
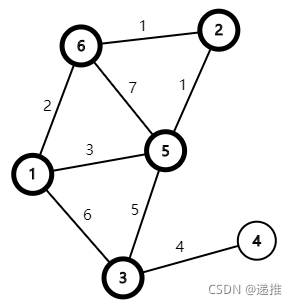
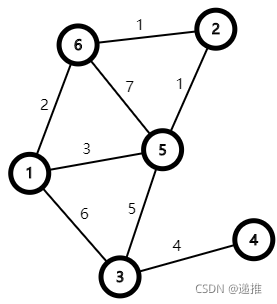
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。
Dijkstra算法 只能用于计算单源最短路，而且无法处理负权边。
时间复杂度：O()
【代码实现】
//假设有n个点，m条边，求1~n的最短路径
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m;
int mapp[1001][1001];//图
int dis[1001];//最短距离
int vis[1001];//是否加入集合
void dijkstra()
{
for(int k=1;k<=n;k++)
{
int minn=0x7f7f7f,pos;
for(int i=1;i<=n;i++)
{
if(!vis[i]&&dis[i]<minn)
{
minn=dis[i],pos=i;//pos为松弛点的坐标，minn为源点到松弛点的值
}
}
vis[pos]=true;
for(int i=1;i<=n;i++)
{
if(!vis[i]&&dis[i]>dis[pos]+mapp[pos][i])//更新dis值
{
dis[i]=dis[pos]+mapp[pos][i];
}
}
}
return;
}
int main()
{
scanf("%d%d",&n,&m);//读入
for(int i=1;i<=m;i++)//读入边的值
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
mapp[u][v]=w;//有向图
//mapp[u][v]=mapp[v][u]=w;无向图
}
dijkstra();
printf("%d",dis[n]);//输出
return 0;
}提到 Dijkstra算法，就要想到它的堆优化。
堆优化的主要思想就是使用一个优先队列（就是每次弹出的元素一定是整个队列中最小的元素）来代替最近距离的查找，用邻接表代替邻接矩阵，这样可以大幅度节约时间开销。这样以来，就需要用到链式前向星的存储方式来存图。
引入一道例题：洛谷 P3371 【模板】单源最短路径（弱化版）
一道 Dijkstra算法+堆优化 的模板题，直接上代码！
【代码实现】
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;//小根堆
int fir[500001],to[500001],val[500001],nex[500001],n,m,s,u,v,w,cnt;
const int inf=2147483647;
long long dis[10001];
bool book[100001];
void add(int a,int b,int c)//链式前向星
{
to[++cnt]=b;
val[cnt]=c;
nex[cnt]=fir[a];
fir[a]=cnt;
}
int main()
{
cin>>n>>m>>s;//读入
for(int i=1; i<=m; i++)//读图
{
cin>>u>>v>>w;
add(u,v,w);
}
for(int i=1; i<=n; i++)//初始化
{
dis[i]=inf;
}
dis[s]=0;
q.push(make_pair(0,s));//根节点入队
while(q.size())//Dijkstra算法+堆优化 的模板
{
int x=q.top().second;
q.pop();
if(book[x]) continue;
book[x]=1;
for(int i=fir[x]; i; i=nex[i])
{
if(dis[to[i]]>dis[x]+val[i])
{
dis[to[i]]=dis[x]+val[i];
q.push(make_pair(dis[to[i]],to[i]));
}
}
}
for(int i=1;i<=n;i++)//输出
{
cout<<dis[i]<<" ";
}
return 0;
}Bellman-Ford算法 \ SPFA算法：
贝尔曼-福特（Bellman-Ford）是由 理查德·贝尔曼（Richard Bellman）和 莱斯特·福特 创立的，求解单源最短路径问题的一种算法。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行V-1次松弛操作，得到所有可能的最短路径。其优于 Dijkstra 算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高。但算法可以进行若干种优化，提高效率。
时间复杂度：O(VE)
【代码实现】
//假设有n个点，m条边，求s~n的最短路径
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m,s;
long long dis[1001];//最短距离
int u[1001],v[1001],w[1001];//存储图
int main()
{
scanf("%d %d %d",&n,&m,&s);//读入
for(int i=1;i<=n;i++)//初始化
{
dis[i]=0x7f7f7f;
}
dis[s]=0;
for(int i=1;i<=m;i++)//读图
{
scanf("%d%d%d",&u[i],&v[i],&w[i]);
}
for(int k=1;k<=n-1;k++)//Bellman-Ford算法 模板
{
int flag=0;
for(int i=1;i<=m;i++)
{
if(dis[v[i]]>dis[u[i]]+w[i])
{
dis[v[i]]=dis[u[i]]+w[i];
flag=1;
}
}
if(!flag)
{
break;
}
}
printf("%lld\n",dis[n]);//输出
return 0;
}显然，O(VE)的时间复杂度是不会被 Orz 们认可的，于是，就有了 SPFA 算法，也就是Bellman-Ford算法 的队列优化算法。
SPFA算法 的时间复杂度通常是：O(kE)，k是常数。但在最坏情况下，SPFA算法的时间复杂度会和普通 Bellman-Ford算法 的时间复杂度相同，为：O(VE)
【代码实现】
//假设有n个点，m条边，求s~n的最短路径
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m,tot;
struct node//链式前向星
{
int next;
int v;
int w;
}mapp[1001];
int head[1001];
int dis[1001];//最短距离
bool vis[1001];//标记
void spfa(int st)//st是源点
{
memset(vis,false,sizeof(vis));//初始化
memset(dis,0x7f7f7f,sizeof(dis));//初始化
queue<int>q;//队列
dis[st]=0;//源点的距离默认成0
vis[st]=true;//标记源点
q.push(st);//放入队列
while(!q.empty())
{
int u=q.front(); //弹出当前点
q.pop();
vis[u]=false;
for(int i=head[u];i!=-1;i=mapp[i].next)
{
int v=mapp[i].v;
int w=mapp[i].w;
if (dis[v]>dis[u]+w) //比较子节点距离源点的距离和（父节点距离源点的距离+他们之间的距离）
{
dis[v]=dis[u]+w; //如果子节点距离源点的距离可以更小，则更新子节点的距离源点的距离
if (!vis[v]) //如果子节点未被标记过，则标记子节点，并加入队列
{
vis[v]=true;
q.push(v);
}
}
}
}
}
void add(int u,int v,int w)//链式前向星
{
++tot;
mapp[tot].next=head[u];
mapp[tot].v=v;
mapp[tot].w=w;
head[u]=tot;
return;
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);//读入
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);//有向图
//add(u,v,w),add(v,u,w);无向图
}
spfa(1);//spfa算法 模板
printf("%d",dis[n]);//输出
return 0;
}Johnson算法：
Johson算法是目前最高效的在无负环可带负权重的网络中求所有点对最短路径的算法。
Johnson算法主要用于求稀疏图上的全源最短路径，其主体思想是利用重赋权值的方法把一个愿问题带负权的图转化为权值非负的图，然后再利用N NN次D i j k s t r a DijkstraDijkstra求出全源最短路径。
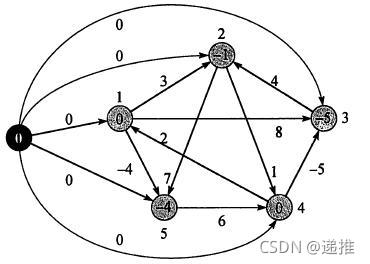
引入一道例题：洛谷 P5905 【模板】Johnson 全源最短路
一道 Johnson算法 的模板题（这里不再展示代码，自己写吧，实在不会，洛谷也有题解）。
A*算法：
A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。
再次引入一道例题：洛谷 P1379 八数码难题
一道 A*算法 的模板题，直接套用模板就可以（代码不再展示，不会可以查题解）。
扫一扫
6430
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
