6.1 线段求交
首先对地图叠合问题的最简单形式做一讨论。也就是说,(相互叠合的)两个地图层,分别都是由一组线段表示的某个网络。以图为例,可能有若干小比例图层分别存放道路、铁路和河流信息。

这些线段将导出的一些子区域,不过在此我们对这些子区域并不感兴趣。后面将会考虑更为复杂的情况——(相互叠合的)地图不是网络,而是平面经过子区域划分之后导出的、具有明确含义的一些子区域。
6.1.1 为解决网络叠合的问题,首先需要用几何的概念来描述这一问题。
就两个网络的叠合而言,对应的几何条件是这样的:给定由线段组成的两个集合,计算出来自于其中一个集合的所有线段,与来自于另一个集合的所有线段之间的交点。
为了做进一步简化,我们还将把分别来自两个集合的线段合到一起,构成一个集合,然后来考虑其中所有线段之间的交点。
进而将问题定义为:给定由平面上n条闭线段构成的一个集合S,报告出S中各线段之间的所有交点。
乍看起来,这个问题并没有什么挑战性——可以依次检查每一对线段,看看它们是否相交;如果的确相交,就将其交点报告出来。显然,这种直截了当式的算法需要O(n2)时间。就某种意义而言,这个结果甚至是最优的:若如图所示,每两条线段都相交,那么无论采用什么算法,至少都需要Ω(n2)时间。

在实际的环境中,大多数的线段要么根本不与其他线段相交,要么只与少数的线段相交,因此,交点的总数远远达不到平方量级。因此,我们希望得到的算法,其运行时间不仅取决于输入中线段的数目,还取决于(实际的)交点数目。这样的算法,被称为"输出敏感的"算法(output-sensitive-algorithm)。
6.1.2 交点敏感的算法
在找出所有交点的过程中,如何才能避免对所有的线段对进行测试呢?这里必须利用这种情况的几何特性——只有那些相互靠近的线段,才可能会相交;而相距甚远的线段则不可能相交。
设需要对其进行求交的线段构成集合S:={s1,s2,…,sn},首先排除一种简单的情况,如图所示,将一条线段在y轴上的正交投影,定义为它的y区间(y-interval)。

任何两条线段,只要其y区间没有重叠部分——此时,也可以说,它们在y方向上相距很远——它们就一定不会相交。这样,只需要对那些y区间相互有所重叠(即与同一条垂线相交)的线段对进行测试。
平面扫描算法(plane sweep algorithm)
为找出这些线段对,可以想象着用一条直线l,从一个高于所有线段的位置起,自上而下地扫过整个平面。在这条假象的直线扫过平面的过程中,跟踪记录所有与之相交的线段——以找出所需的所有线段对。
在算法中,使用的直线l被称为扫描线(sweep line)。与当前扫描线相交的所有线段构成的集合,被称为扫描线的状态(status)。
只有在某些特定的位置,才需要对扫描线的状态进行更新。我们称这些位置为平面扫描算法的事件点(event point)。就本算法而言,这里的事件点就是各线段的端点。
事件点
只有在扫描线触及某个事件点的时候,算法才会进行实质的处理——更新扫描线的状态,并进行一些相交测试。具体而言:
-
上端点
若事件点为某个线段的上端点,则意味着这条直线段将开始与扫描线相交,因此需要将该线段插入到状态结构(status structure)中。然后,需要将这条线段,和那些与当前扫描线相交的其他线段分别进行测试,确定是否相交。
-
下端点
若事件点为某个线段的下断点,则意味着这条线段将不再与扫描线相交,因此需要将该线段从状态结构中删去。
局限性
按照这样的方式,只需要对那些可能与某条水平直线同时相交的线段进行测试。不幸的是,这还不够——因为,在某些(特殊的)情况下,尽管实际的交点数目很少,却依然需要对平方量级的线段进行测试。
一个简单例子就是,所有线段都是垂直的,而且都与x坐标轴相交。因此,目前的这个算法还算不上是输出敏感的。
问题在于,与同一扫描线相交的两条线段,在水平方向上仍然有可能相距很远。
临近性考虑
当考虑到水平方向的临近性后,可以沿着扫描线,将与之相交的所有线段自左向右排序。
这样,只有当其中的某两条线段沿水平方向相邻时,才需要对其进行测试。这就意味着,每引入一条线段,只需要将其与另外的两条线段(具体地讲,就是与新线段上端点左、右紧邻的那两条线段)进行测试。此后,当扫描线向下推进到某个新的位置时,与某条线段紧邻的邻居有可能会发生变化,此时,也需将它与新的邻居进行测试。
在算法的状态结构中,这一新策略应该有所反映——状态结构不仅要记录与当前扫描线相交的所有线段,而且还要对这些线段排序。

在将这些构思落实为高效的算法之前,需要确定,这种方法正确。验证之前,首先忽略掉一些"棘手"的情况——假设:没有水平线段;任何两条线段最多相交于一点(也就是说,任何两条线段都不会有局部的相互重叠);任何三条线段不会相较于一点。虽然上述假设情况,很容易处理,但是为了更好的论证,目前先置之不理的好。
对于,某线段端点落在另一条线段上的情况,等到扫描线触及相应端点时,这类交点也会被检测。
因此,目前唯一剩下的问题:线段之间的每一交点,是否能被进行检测?
引理
设两条非水平的线段si和sj只相交于其内部的一点p,而且,任何第三条线段都不经过p。则在(扫描线到达)高于p的某个事件点处(时),si和sj必然会彼此紧邻,并因此接受相交测试(于是对应的交点将被发现)。
证明
如图所示,令l为比p略高的一条水平线。只要l与p相距足够近,则沿着l、si和sj必然是紧邻的(更准确地说,没有任何事件点落在我们所取的l上,而且也没有任何事件点夹在l与通过p的水平线之间)。
总而言之,必然存在某个位置,当扫描线到达这个位置时,si和sj是紧邻的。另一方面,在算法开始的时刻,si和sj并不是紧邻的——此时,扫描线的位置比所有的线段都高,故状态结构还是空的。因此,必然存在某个事件点q,在q的位置,si和sj开始变为紧邻的,从而接受相交测试。
事件点添加新成员
就目前而言,事件点既包括(事先就可以确定的)各线段端点,也包括(在算法运行过程中逐步发现的)交点。
在扫描线移动的过程中,要维护一个有序序列,该序列由所有与当前扫描线相交的线段组成。每遇到一个事件点,都会通过一些动作,对状态结构进行更新,并检测出新的交点——具体的处置方法,取决于事件点类型。
-
上端点
事件点为上端点,意味着将有一条新的线段开始与扫描线相交,如下图所示。

新引入的线段,需测试判断它是否与沿扫描线与之紧邻的另外两条线段相交。
只有位于当前扫描线下方的交点,才需要加以考虑;高于扫描线的交点,必然已经被检测过了。
例如,线段si和sk原本是紧邻的,而(在某个时刻)第三条线段sj的上端点出现在它们之间,则此时就必须分别将sj与si和sk进行测试。在检测出来的(最多两个)交点中,只要位于当前扫描线的下方,就是一个新的事件点。在处理完该上端点之后,将继续考虑下一个事件点。
-
交点
只有位于当前扫描线下方的交点,才是待处理的事件点;位于上方的交点,必然是已经处理完成的事件点。

如图所示,有关的两条相关线段就会交换其(沿扫描线)次序。它们各自可能(最多)有一条新的紧邻线段,因此,必须分别将它们与其各自的新邻居进行测试,以找出可能得交点。
假设在扫描线触及sk和sl的交点那一时刻,有四条线段sj、sk、sl和sm依次出现在扫描线上。此后,sk和sl将交换次序,于是需要分别对sl和sj、sk和sm进行测试,以找出它们可能位于扫描线下方的交点,并添加为事件点(注意,该事件点可能已经被发现——例如,两条线段在此前的一段时间内曾经是紧邻的,后来变得不再紧邻,最终又再次变成是相互紧邻的)。
-
下端点
若事件点为某条线段的下端点,则它此前的(一左一右)两个邻居现在就会变成是相互紧邻的,因此需要对它们进行相交测试。若有交点,且交点位于扫描线的下方,则该交点应添加为事件点(注意,事件点可能已被添加)。

如图,在某一时刻,沿着扫描线,有依次相邻的三条线段sk、sl和sm,扫描线继续前移后遇到了sl的下端点。于是,sk和sm将变成是相互紧邻的。
在平面扫描过程中,如下不变性始终成立:(在任何时刻)处于扫描线上方的所有交点都已经被正确地检测出来。
算法涉及数据结构
-
平衡二分查找树(balanced binary search tree)
平衡二分查找树是一种特殊的二叉搜索树,它在插入或删除节点时通过自动调整结构,保持左右子树高度差不超过一定阈值(通常为1)。这种平衡性保证了树的高度始终为O(log n),从而确保查找、插入、删除等操作的时间复杂度稳定在O(log n)。
常见实现包括:AVL树(由苏联科学家Adelson-Velsky和Landis于1962年发明)、红黑树、Treap等。
以下是AVL树的一般性实现:
#include <iostream> using namespace std; class AVLNode{ public: int key; AVLNode* left; AVLNOde* right; int height; AVLNode(int k):key(k),left(nullptr),right(nullptr),height(1){} }; class AVLTree{ private: AVLNode* root; //获取节点高度 int getHeight(AVLNode* node){ return node ? node->height : 0; } //计算平衡因子 int getBalanceFactor(AVLNode* node){ return node ? getHeight(node->left) - getHeight(node->right) : 0; } //右旋操作 /* Y(失衡节点) X(新根节点) / \ 右旋后 / \ X C ========> A Y / \ / \ A B B C 1. 将X的右子树B挂到Y的左子树位置 2. 将Y挂到X的右子树位置 */ AVLNode* rightRotate(AVLNode* y){ AVLNode* x = y->left; AVLNode* T3 = x->right; x->right = y; y->left = T3; y->height = max(getHeight(y->left),getHeight(y->right)) + 1; x->height = max(getHeight(x->left),getHeight(x->right)) + 1; return x; } //左旋操作 /* X(失衡节点) Y(新根节点) / \ 左旋后 / \ A Y ========> X C / \ / \ B C A B 1.将Y的左子树B挂到X的右子树位置 2.将X挂到Y的左子树位置 */ AVLNode* leftRotate(AVLNode* x){ AVLNode* y = x->right; AVLNode* T2 = y->left; y->left = x; x->right = T2; x->height = max(getHeight(x->left),getHeight(x->right)) + 1; y->height = max(getHeight(y->left),getHeight(y->right)) + 1; return y; } //递归插入节点 AVLNode* insertHelper(AVLNode* node,int key){ if(!node) return new AVLNode(key); if(key < node->key) node->left = insertHelper(node->left,key); else if(key > node->key) node->right = insertHelper(node->right,key); else return node; //不允许重复值 //更新高度 node->height = 1 + max(getHeight(node->left),getHeight(node->right)); //获取平衡因子 int balance = getBalanceFactor(node); //平衡调整(4种情况) //左左情况:当左子树更高且新节点插入到左子树的左侧 //右旋 if(balance > 1 && key < node->left->key) return rightRotate(node); //右右情况:当右子树更高且新节点插入到右子树的右侧 //左旋 if(balance < -1 && key > node->right->key) return leftRotate(node); //左右情况:左子树的右子树引发失衡 //先左后右 if(balance > 1 && key > node->left->key){ node->left = leftRotate(node->left); return rightRotate(node); } //右左情况:右子树的左子树引发失衡 //先右后左 if(balance < -1 && key < node->right->key){ node->right = rightRotate(node->right); return leftRotate(node); } return node; } //中序遍历 void inorderHelper(AVLNode* node){ if(!node) return; inorderHelper(node->left); cout << node->key << " "; inorderHelper(node->right); } public: AVLTree() : root(nullptr){} void insert(int key){ root = insertHelper(root,key); } void printInorder(){ inorderHelper(root); cout << endl; } } -
事件队列(event queue)
来存放(当前已被检测出来,但尚未发生的)事件,使用平衡二分查找树构建。
-
删除操作
把即将发生的下一事件从队列中删除掉,并将它返回(给主程序),以便对它进行处理。
这个事件,是位于扫描线下方、位置最高的那个事件。倘若有两个事件点的y坐标相同,则约定返回x坐标更小的事件点。
按照这一约定,若是一条水平线段,则应该将其左(右)端点视为上(下)端点。
-
插入操作
算法运行的过程中,可能会出现新的事件。请注意,不同事件点的位置可能会重合,位置相同的事件点,当成同一事件点更为合理。
因此插入操作时,必须检查待插入的事件是否已经出现在队列中。
在本算法中,事件点作为key值,需要在事件点之间定义一个次序<进行排序。对于任意两个事件点p和q,定义"p<q当且仅当py>qy,或者py = qy且px<qx"。
对于事件队列中的每一个事件点p,我们同时还应用一个成员变量,记录下起始于p的(也就是以p为其上端点的)那条线段。
应用平衡二分查找树,做取出下一个事件和插入新的事件的操作,时间复杂度O(logn),n为事件队列中事件点数目。
-
-
算法状态
所谓状态,就是与当前扫描线相交的所有线段构成的有序序列;由于在任一时刻,状态结构中的所有线段之间具有一个定义明确的次序,因此可以使用一棵平衡二分查找树来实现状态结构。
借助一个状态结构(status structure),可以访问某一给定线段s的(左、右)邻居,插入s之后,可方便的进行相应的相交测试。它是动态的,一旦有某条线段开始(或不再)与扫描线相交,就应将它插入到状态结构中(或从状态结构中删去)。
在任一时刻,状态结构中的所有线段之间具有一个定义明确的次序,因此可以使用一棵平衡二分查找树来实现状态结构。与当前扫描相交的每条线段,都按照其次序,存放在该平衡二分查找树的某匹叶子处。
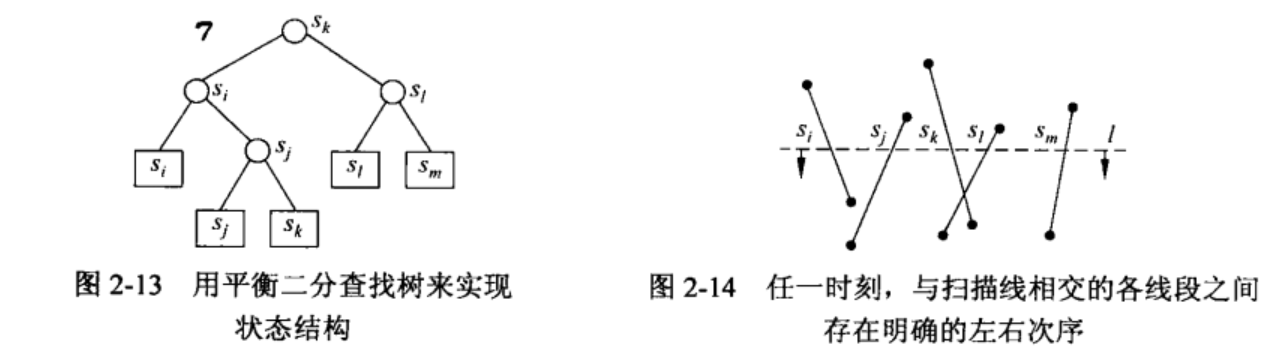
如图所示,各线段沿着扫描线自左向右的次序,与状态结构中各叶子自左向右的次序完全一致。在每个内部节点处,要存放其左子树中的最右端叶子。
假设某个点p正落在扫描线上,我们需要查找紧邻于其左侧的那条线段。在每个内部节点v处,为了判断p是位于线段的左侧还是右侧,只要将p与记录在v处的线段做一次比较。根据比较结果,可以深入到v的左子树或右子树,直到最终到达某匹叶子。
实践中有另一做法:只将各线段存放在这些内部节点处。这种方法可以节省空间。不过,书籍作者认为,从概念上看,将存放在内部节点处的线段想象成用以引导查找的数值,而不是真正的数据项,将使算法更加易于理解。将线段存放在叶子处,也可以使算法的描述更加简明。
不过本人水平有限,下面代码示例,用的是线段存放内部节点的做法。
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <limits>
#include <memory>
#include <cassert>
#include <optional>
#include <set>
using namespace std;
#define fTOL 1e-6
// 点结构体
struct Point {
double x, y;
Point(double x = 0, double y = 0) : x(x), y(y) {}
bool operator==(const Point& other) const {
return fabs(x - other.x) < fTOL && fabs(y - other.y) < fTOL;
}
bool operator!=(const Point& other) const {
return !(*this == other);
}
};
// 线段结构体
struct Segment {
Point upper, lower; // 上端点和下端点
Segment(Point p1, Point p2) {
if (p1.y > p2.y || (p1.y == p2.y && p1.x < p2.x)) {
upper = p1;
lower = p2;
} else {
upper = p2;
lower = p1;
}
}
// 判断点是否在线段上
bool contains(const Point& p) const {
// 检查y坐标范围
if (p.y < min(lower.y, upper.y) - fTOL ||
p.y > max(lower.y, upper.y) + fTOL) {
return false;
}
// 处理水平线段
if (fabs(upper.y - lower.y) < fTOL) {
return p.x >= min(upper.x, lower.x) - fTOL &&
p.x <= max(upper.x, lower.x) + fTOL;
}
// 处理垂直线段
if (fabs(upper.x - lower.x) < fTOL) {
return fabs(p.x - upper.x) < fTOL;
}
// 一般情况:计算参数t并检查x坐标
double t = (p.y - lower.y) / (upper.y - lower.y);
if (t < -fTOL || t > 1 + fTOL) return false;
double x = lower.x + t * (upper.x - lower.x);
return fabs(x - p.x) < fTOL;
}
bool operator==(const Segment& other) const {
return (upper == other.upper && lower == other.lower) ||
(upper == other.lower && lower == other.upper);
}
bool operator<(const Segment& other) const {
// 比较线段的端点坐标,确保唯一性
auto comparePoints = [](const Point& a, const Point& b) {
return (a.x != b.x) ? (a.x < b.x) : (a.y < b.y);
};
// 获取当前线段的最小和最大端点
Point min1 = comparePoints(upper, lower) ? upper : lower;
Point max1 = comparePoints(upper, lower) ? lower : upper;
// 获取比较线段的最小和最大端点
Point min2 = comparePoints(other.upper, other.lower) ? other.upper : other.lower;
Point max2 = comparePoints(other.upper, other.lower) ? other.lower : other.upper;
// 先比较最小端点,再比较最大端点
if (min1 != min2) return comparePoints(min1, min2);
return comparePoints(max1, max2);
}
// 计算两条线段的交点
static Point* computeIntersection(const Segment& s1, const Segment& s2) {
// 检查零长度线段
if (s1.upper == s1.lower || s2.upper == s2.lower) {
return nullptr;
}
Point a1 = s1.upper, a2 = s1.lower;
Point b1 = s2.upper, b2 = s2.lower;
// 特殊处理水平线段
if (fabs(a1.y - a2.y) < fTOL) { // s1是水平线段
if (fabs(b1.y - b2.y) < fTOL) { // s2也是水平线段
// 两条水平线段,检查是否共线且有重叠
if (fabs(a1.y - b1.y) > fTOL) return nullptr;
double minX1 = min(a1.x, a2.x);
double maxX1 = max(a1.x, a2.x);
double minX2 = min(b1.x, b2.x);
double maxX2 = max(b1.x, b2.x);
if (maxX1 < minX2 - fTOL || maxX2 < minX1 - fTOL) return nullptr;
// 返回任意重叠点
double x = max(minX1, minX2);
return new Point(x, a1.y);
} else {
// s1水平,s2非水平
// 检查s2是否与水平线y=a1.y相交
if ((b1.y - a1.y) * (b2.y - a1.y) > fTOL) return nullptr;
double t = (a1.y - b1.y) / (b2.y - b1.y);
if (t < -fTOL || t > 1 + fTOL) return nullptr;
double x = b1.x + t * (b2.x - b1.x);
double minX = min(a1.x, a2.x) - fTOL;
double maxX = max(a1.x, a2.x) + fTOL;
if (x >= minX && x <= maxX) {
return new Point(x, a1.y);
}
}
} else if (fabs(b1.y - b2.y) < fTOL) { // s2是水平线段
// s2水平,s1非水平
if ((a1.y - b1.y) * (a2.y - b1.y) > fTOL) return nullptr;
double t = (b1.y - a1.y) / (a2.y - a1.y);
if (t < -fTOL || t > 1 + fTOL) return nullptr;
double x = a1.x + t * (a2.x - a1.x);
double minX = min(b1.x, b2.x) - fTOL;
double maxX = max(b1.x, b2.x) + fTOL;
if (x >= minX && x <= maxX) {
return new Point(x, b1.y);
}
} else {
// 通用情况:两条线段都不是水平的
double dxa = a2.x - a1.x, dya = a2.y - a1.y;
double dxb = b2.x - b1.x, dyb = b2.y - b1.y;
double det = dxa * dyb - dya * dxb;
if (fabs(det) < fTOL) return nullptr; // 平行或共线
double u = ((b1.x - a1.x) * dyb - (b1.y - a1.y) * dxb) / det;
double v = ((b1.x - a1.x) * dya - (b1.y - a1.y) * dxa) / det;
if (u >= 0 && u <= 1 && v >= 0 && v <= 1) {
return new Point(a1.x + u * dxa, a1.y + u * dya);
}
}
return nullptr;
}
};
// 事件点比较函数
struct EventPointCompare {
bool operator()(const Point& p, const Point& q) const {
if (p.y != q.y) return p.y > q.y; // y坐标大的优先
return p.x < q.x; // y相同时,x小的优先
}
};
// 平衡二叉搜索树节点模板
template <typename T, typename Compare = less<T>>
struct AVLNode {
T key;
shared_ptr<AVLNode<T, Compare>> left, right;
int height;
shared_ptr<AVLNode<T, Compare>> max_right; // 用于状态结构中存储最右叶子
AVLNode(const T& key) : key(key), left(nullptr), right(nullptr), height(1), max_right(nullptr) {}
};
// 平衡二叉搜索树模板
template <typename T, typename Compare = less<T>>
class AVLTree {
private:
shared_ptr<AVLNode<T, Compare>> root;
Compare comp;
// 获取节点高度
int height(shared_ptr<AVLNode<T, Compare>> node) const {
return node ? node->height : 0;
}
// 更新节点高度
void updateHeight(shared_ptr<AVLNode<T, Compare>> node) {
if (node) {
node->height = 1 + max(height(node->left), height(node->right));
}
}
// 获取平衡因子
int balanceFactor(shared_ptr<AVLNode<T, Compare>> node) const {
return height(node->left) - height(node->right);
}
// 右旋转
shared_ptr<AVLNode<T, Compare>> rotateRight(shared_ptr<AVLNode<T, Compare>> y) {
auto x = y->left;
auto T2 = x->right;
x->right = y;
y->left = T2;
updateHeight(y);
updateHeight(x);
return x;
}
// 左旋转
shared_ptr<AVLNode<T, Compare>> rotateLeft(shared_ptr<AVLNode<T, Compare>> x) {
auto y = x->right;
auto T2 = y->left;
y->left = x;
x->right = T2;
updateHeight(x);
updateHeight(y);
return y;
}
// 平衡节点
shared_ptr<AVLNode<T, Compare>> balance(shared_ptr<AVLNode<T, Compare>> node) {
if (!node) return nullptr;
updateHeight(node);
int bf = balanceFactor(node);
// 左左情况
if (bf > 1 && balanceFactor(node->left) >= 0) {
return rotateRight(node);
}
// 左右情况
if (bf > 1 && balanceFactor(node->left) < 0) {
node->left = rotateLeft(node->left);
return rotateRight(node);
}
// 右右情况
if (bf < -1 && balanceFactor(node->right) <= 0) {
return rotateLeft(node);
}
// 右左情况
if (bf < -1 && balanceFactor(node->right) > 0) {
node->right = rotateRight(node->right);
return rotateLeft(node);
}
return node;
}
// 插入辅助函数
shared_ptr<AVLNode<T, Compare>> insertHelper(shared_ptr<AVLNode<T, Compare>> node, const T& key) {
if (!node) return make_shared<AVLNode<T, Compare>>(key);
if (comp(key, node->key)) {
node->left = insertHelper(node->left, key);
} else if (comp(node->key, key)) {
node->right = insertHelper(node->right, key);
} else {
return node; // 重复键
}
return balance(node);
}
// 查找最小节点
shared_ptr<AVLNode<T, Compare>> findMin(shared_ptr<AVLNode<T, Compare>> node) const {
while (node && node->left) {
node = node->left;
}
return node;
}
// 删除辅助函数
shared_ptr<AVLNode<T, Compare>> removeHelper(shared_ptr<AVLNode<T, Compare>> node, const T& key) {
if (!node) return nullptr;
if (comp(key, node->key)) {
node->left = removeHelper(node->left, key);
} else if (comp(node->key, key)) {
node->right = removeHelper(node->right, key);
} else {
if (!node->left || !node->right) {
node = node->left ? node->left : node->right;
} else {
auto temp = findMin(node->right);
node->key = temp->key;
node->right = removeHelper(node->right, temp->key);
}
}
return balance(node);
}
// 查找辅助函数
shared_ptr<AVLNode<T, Compare>> findHelper(shared_ptr<AVLNode<T, Compare>> node, const T& key) const {
if (!node) return nullptr;
if (comp(key, node->key)) {
return findHelper(node->left, key);
} else if (comp(node->key, key)) {
return findHelper(node->right, key);
} else {
return node;
}
}
// 中序遍历辅助函数
void inorderHelper(shared_ptr<AVLNode<T, Compare>> node, vector<T>& result) const {
if (!node) return;
inorderHelper(node->left, result);
result.push_back(node->key);
inorderHelper(node->right, result);
}
public:
AVLTree() : root(nullptr), comp() {}
// 插入元素
void insert(const T& key) {
root = insertHelper(root, key);
}
// 删除元素
void remove(const T& key) {
root = removeHelper(root, key);
}
// 查找元素
bool contains(const T& key) const {
return findHelper(root, key) != nullptr;
}
// 获取最小元素
T findMin() const {
auto node = findMin(root);
if (!node) throw runtime_error("Tree is empty");
return node->key;
}
// 删除并返回最小元素
T extractMin() {
T minVal = findMin();
remove(minVal);
return minVal;
}
// 判断树是否为空
bool empty() const {
return !root;
}
// 中序遍历
vector<T> inorder() const {
vector<T> result;
inorderHelper(root, result);
return result;
}
};
// 事件队列
class EventQueue {
private:
AVLTree<Point, EventPointCompare> tree;
vector<Segment> segments; // 存储所有线段
public:
// 添加事件点
void addEvent(const Point& p, const Segment& s) {
if (!tree.contains(p)) {
tree.insert(p);
}
}
// 获取下一个事件点
Point nextEvent() {
if (tree.empty()) {
throw runtime_error("Event queue is empty");
}
return tree.findMin();
}
// 移除下一个事件点
Point extractNextEvent() {
if (tree.empty()) {
throw runtime_error("Event queue is empty");
}
Point p = tree.findMin();
tree.remove(p);
return p;
}
// 判断队列是否为空
bool empty() const {
return tree.empty();
}
// 获取所有事件点
vector<Point> getAllEvents() const {
return tree.inorder();
}
};
// 线段比较函数(用于状态结构)
struct SegmentCompare {
double scanlineY; // 当前扫描线的y坐标
SegmentCompare() : scanlineY(0) {}
SegmentCompare(double y) : scanlineY(y) {}
// 比较两条线段在当前扫描线位置的x坐标
bool operator()(const Segment& s1, const Segment& s2) const {
double x1 = getXAtScanline(s1);
double x2 = getXAtScanline(s2);
return x1 + fTOL < x2;
}
// 计算线段在扫描线位置的x坐标
double getXAtScanline(const Segment& s) const {
if (s.upper.y == s.lower.y) { // 水平线段
return min(s.upper.x, s.lower.x);
}
if (fabs(scanlineY - s.upper.y) < fTOL) return s.upper.x;
if (fabs(scanlineY - s.lower.y) < fTOL) return s.lower.x;
double t = (scanlineY - s.lower.y) / (s.upper.y - s.lower.y);
return s.lower.x + t * (s.upper.x - s.lower.x);
}
};
// 算法状态结构
class StatusStructure {
private:
AVLTree<Segment, SegmentCompare> tree;
double currentScanlineY;
public:
StatusStructure(double initialY) : currentScanlineY(initialY), tree() {
tree = AVLTree<Segment, SegmentCompare>();
}
// 更新扫描线位置
void updateScanline(double y) {
currentScanlineY = y;
// 不再重置整个树,保持现有线段
}
// 插入线段
void insert(const Segment& s) {
tree.insert(s);
}
// 删除线段
void remove(const Segment& s) {
tree.remove(s);
}
// 查找线段
bool contains(const Segment& s) const {
return tree.contains(s);
}
// 获取线段的前驱
Segment* predecessor(const Segment& s) const {
vector<Segment> allSegs = tree.inorder();
Segment* prev = nullptr;
SegmentCompare comp(currentScanlineY);
for (auto& seg : allSegs) {
if (comp(seg, s)) {
prev = &seg;
} else {
break;
}
}
return prev;
}
// 获取线段的后继
Segment* successor(const Segment& s) const {
vector<Segment> allSegs = tree.inorder();
bool found = false;
SegmentCompare comp(currentScanlineY);
for (auto& seg : allSegs) {
if (found) {
return &seg;
}
if (comp(seg, s)) {
found = true;
}
}
return nullptr;
}
// 查找包含点的线段
Segment* findSegmentContaining(const Point& p) const {
vector<Segment> allSegs = tree.inorder();
for (auto& seg : allSegs) {
if (seg.contains(p)) {
return &seg;
}
}
return nullptr;
}
// 获取所有线段
vector<Segment> getAllSegments() const {
return tree.inorder();
}
};
// 相交记录结构体
struct IntersectionRecord {
Segment seg1;
Segment seg2;
Point intersection;
IntersectionRecord(const Segment& s1, const Segment& s2, const Point& p)
: seg1(s1), seg2(s2), intersection(p) {}
bool operator<(const IntersectionRecord& other) const {
if (fabs(seg1.upper.x - other.seg1.upper.x) >= fTOL) return seg1.upper.x < other.seg1.upper.x;
if (fabs(seg1.upper.y - other.seg1.upper.y) >= fTOL) return seg1.upper.y < other.seg1.upper.y;
if (fabs(seg2.upper.x - other.seg2.upper.x) >= fTOL) return seg2.upper.x < other.seg2.upper.x;
if (fabs(seg2.upper.y - other.seg2.upper.y) >= fTOL) return seg2.upper.y < other.seg2.upper.y;
if (fabs(intersection.x - other.intersection.x) >= fTOL) return intersection.x < other.intersection.x;
return intersection.y + fTOL < other.intersection.y;
}
bool operator==(const IntersectionRecord& other) const {
return (seg1 == other.seg1 && seg2 == other.seg2 && intersection == other.intersection) ||
(seg1 == other.seg2 && seg2 == other.seg1 && intersection == other.intersection);
}
};
// 平面扫描算法
class PlaneSweep
{
private:
EventQueue eventQueue;
StatusStructure status;
vector<Segment> segments;
set<IntersectionRecord> intersections; // 使用set自动去重
public:
PlaneSweep(const vector<Segment> &inputSegments) : status(numeric_limits<double>::max())
{
segments = inputSegments;
// 初始化事件队列
for (const auto &seg : segments)
{
eventQueue.addEvent(seg.upper, seg); // 上端点
eventQueue.addEvent(seg.lower, seg); // 下端点
}
}
// 运行平面扫描算法
void run()
{
while (!eventQueue.empty())
{
Point p = eventQueue.extractNextEvent();
cout << "\nProcessing event at (" << p.x << ", " << p.y << ")" << endl;
// 更新扫描线位置
status.updateScanline(p.y);
// 处理事件点
handleEventPoint(p);
// 打印当前状态
cout << "Current segments in status:" << endl;
vector<Segment> currentSegs = status.getAllSegments();
for (const auto& seg : currentSegs) {
cout << "(" << seg.upper.x << "," << seg.upper.y << ")-("
<< seg.lower.x << "," << seg.lower.y << ")" << endl;
}
}
}
// 获取所有相交记录
set<IntersectionRecord> getIntersections() const {
return set<IntersectionRecord>(intersections.begin(), intersections.end());
}
private:
// 处理事件点
void handleEventPoint(const Point &p)
{
vector<Segment> U, L, C;
// 分类线段
for (const auto &seg : segments)
{
if (seg.upper == p)
{
U.push_back(seg); // 以p为上端点的线段
}
else if (seg.lower == p)
{
L.push_back(seg); // 以p为下端点的线段
}
else if (seg.contains(p))
{
// 对于水平线段,如果p在端点,已经包含在U/L中
if (!(fabs(seg.upper.y - seg.lower.y) < fTOL &&
(p == seg.upper || p == seg.lower))) {
C.push_back(seg); // 包含p的线段
}
}
}
// 特殊处理水平线段
for (const auto &seg : segments) {
if (fabs(seg.upper.y - seg.lower.y) < fTOL &&
seg.contains(p)) {
// 水平线段且包含当前事件点
if (!(seg.upper == p || seg.lower == p)) {
C.push_back(seg);
}
// 检查与所有当前活动线段的交点
for (const auto& activeSeg : status.getAllSegments()) {
if (fabs(activeSeg.upper.y - activeSeg.lower.y) > fTOL) { // 非水平线段
Point* intersection = Segment::computeIntersection(seg, activeSeg);
if (intersection && *intersection != p) {
bool exists = false;
for (const auto& record : intersections) {
if ((record.seg1 == seg && record.seg2 == activeSeg) ||
(record.seg1 == activeSeg && record.seg2 == seg)) {
exists = true;
break;
}
}
if (!exists) {
intersections.insert(IntersectionRecord(seg, activeSeg, *intersection));
eventQueue.addEvent(*intersection, seg);
}
delete intersection;
}
}
}
}
}
// 处理线段交点
if (U.size() + L.size() + C.size() > 1) {
// 检查所有可能的线段对组合
vector<Segment> allSegs;
allSegs.insert(allSegs.end(), U.begin(), U.end());
allSegs.insert(allSegs.end(), L.begin(), L.end());
allSegs.insert(allSegs.end(), C.begin(), C.end());
// 使用set去重线段并遍历所有唯一组合
set<Segment> uniqueSegs(allSegs.begin(), allSegs.end());
vector<Segment> uniqueVec(uniqueSegs.begin(), uniqueSegs.end());
for (size_t i = 0; i < uniqueVec.size(); ++i) {
for (size_t j = i + 1; j < uniqueVec.size(); ++j) {
// 检查是否已经记录过这个交点
bool exists = false;
for (const auto& record : intersections) {
if ((record.seg1 == uniqueVec[i] && record.seg2 == uniqueVec[j]) ||
(record.seg1 == uniqueVec[j] && record.seg2 == uniqueVec[i])) {
exists = true;
break;
}
}
if (!exists) {
intersections.insert(IntersectionRecord(uniqueVec[i], uniqueVec[j], p));
}
}
}
}
// 从状态结构中移除L和C线段
for (const auto &seg : L)
{
if (status.contains(seg))
{
status.remove(seg);
}
}
for (const auto &seg : C)
{
if (status.contains(seg))
{
status.remove(seg);
}
}
// 将U和C线段插入状态结构
for (const auto &seg : U)
{
status.insert(seg);
}
for (const auto &seg : C)
{
status.insert(seg);
}
// 检查所有相邻线段的交点
vector<Segment> currentSegments = status.getAllSegments();
// cout << "===================" << endl;
// cout << "EventPt: (" << p.x << "," << p.y << ")" << endl;
// cout << "currentSegments Num:" << currentSegments.size() << endl;
for (size_t i = 1; i < currentSegments.size(); i++)
{
Segment *left = ¤tSegments[i - 1];
Segment *right = ¤tSegments[i];
// cout << "intersection left seg: (" << left->upper.x << "," << left->upper.y << ")-("
// << left->lower.x << "," << left->lower.y << ")" << endl;
// cout << "intersection right seg: (" << right->upper.x << "," << right->upper.y << ")-("
// << right->lower.x << "," << right->lower.y << ")" << endl;
Point *intersection = Segment::computeIntersection(*left, *right);
if (intersection && *intersection != p)
{ // 避免重复处理当前事件点
// cout << "Found internal intersection at (" << intersection->x
// << ", " << intersection->y << ")" << endl;
intersections.insert(IntersectionRecord(*left, *right, *intersection));
// 只添加一次交点事件
eventQueue.addEvent(*intersection, *left);
delete intersection;
}
}
// 获取新插入线段的最左和最右
Segment *leftMost = nullptr;
Segment *rightMost = nullptr;
if (!U.empty())
{
leftMost = &U.front();
rightMost = &U.back();
}
if (!C.empty())
{
if (!leftMost || SegmentCompare(p.y)(C.front(), *leftMost))
{
leftMost = &C.front();
}
if (!rightMost || SegmentCompare(p.y)(*rightMost, C.back()))
{
rightMost = &C.back();
}
}
// 检查与新邻居的交点
if (leftMost)
{
Segment *leftNeighbor = status.predecessor(*leftMost);
if (leftNeighbor)
{
Point *intersection = Segment::computeIntersection(*leftNeighbor, *leftMost);
if (intersection && *intersection != p)
{
// cout << "Found intersection at (" << intersection->x
// << ", " << intersection->y << ")" << endl;
// // 记录相交信息
// cout << "leftNeighbor Adding to intersection: (" << leftNeighbor->upper.x << "," << leftNeighbor->upper.y << ")-("
// << leftNeighbor->lower.x << "," << leftNeighbor->lower.y << ")" << endl;
// cout << "leftMost Adding to intersection: (" << leftMost->upper.x << "," << leftMost->upper.y << ")-("
// << leftMost->lower.x << "," << leftMost->lower.y << ")" << endl;
intersections.insert(IntersectionRecord(*leftNeighbor, *leftMost, *intersection));
eventQueue.addEvent(*intersection, *leftNeighbor);
delete intersection;
}
}
}
if (rightMost)
{
Segment *rightNeighbor = status.successor(*rightMost);
if (rightNeighbor)
{
Point *intersection = Segment::computeIntersection(*rightMost, *rightNeighbor);
if (intersection && *intersection != p)
{
// cout << "Found intersection at (" << intersection->x
// << ", " << intersection->y << ")" << endl;
// // 记录相交信息
// cout << "rightMost Adding to intersection: (" << rightMost->upper.x << "," << rightMost->upper.y << ")-("
// << rightMost->lower.x << "," << rightMost->lower.y << ")" << endl;
// cout << "rightNeighbor Adding to intersection: (" << rightNeighbor->upper.x << "," << rightNeighbor->upper.y << ")-("
// << rightNeighbor->lower.x << "," << rightNeighbor->lower.y << ")" << endl;
intersections.insert(IntersectionRecord(*rightMost, *rightNeighbor, *intersection));
eventQueue.addEvent(*intersection, *rightMost);
delete intersection;
}
}
}
}
};
int main() {
// 创建测试线段
vector<Segment> segments = {
Segment(Point(1, 5), Point(4, 2)), // 线段1
Segment(Point(3, 6), Point(6, 2)), // 线段2
Segment(Point(2, 4), Point(5, 6)), // 线段3
Segment(Point(0, 3), Point(7, 3)) // 水平线段
};
// 运行平面扫描算法
PlaneSweep ps(segments);
ps.run();
// 打印所有相交记录
cout << "\nIntersection Report:" << endl;
cout << "===================" << endl;
cout << "Total intersections found: " << ps.getIntersections().size() << endl;
cout << "===================" << endl;
for (const auto& record : ps.getIntersections()) {
cout << "\nSegment 1: (" << record.seg1.upper.x << ", " << record.seg1.upper.y << ")-("
<< record.seg1.lower.x << ", " << record.seg1.lower.y << ")" << endl;
cout << "Segment 2: (" << record.seg2.upper.x << ", " << record.seg2.upper.y << ")-("
<< record.seg2.lower.x << ", " << record.seg2.lower.y << ")" << endl;
cout << "Intersection Point: (" << record.intersection.x << ", " << record.intersection.y << ")" << endl;
cout << "-------------------" << endl;
}
return 0;
}






















 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








