4.1 凸包定义
平面的一个子集S被称为是"凸"的,当且仅当对于任意两点
p,q∈S
p,q\in S
p,q∈S
线段pq都完全属于S。集合S的凸包Conv(S),就是包含S的最小凸集。

这里所要讨论的,是如何计算平面上由n个点组成的有限集合P的凸包。可以借助一个虚构式实验,来想像这种凸包的模样:将这里的点想像成钉在平面上的钉子;取来一根橡皮绳,将它撑开围住所有的钉子,然后松开手——啪的一声,橡皮绳将紧绷到钉子上,它的总长度也将达到最小。此时,由橡皮绳围住的区域就是P的凸包。

因此,可将平面有限点集P的凸包定义为:顶点取自于P且包含P中所有点的那个唯一凸边形(convex polygon)。
4.2 凸包计算
P的凸包是一个凸多边形。表示多边形的一种自然的方法,就是从任一顶点开始,沿顺时针方向依次列出所有顶点。
给定平面点集P={p1,…,pn},通过计算从P中选出若干点,它们沿顺时针方向依次对应于conv§的各个顶点。
input = 平面上一组点:p1,p2,p3,p4,p5,p6,p7,p8,p9
output = 凸包的表示:

SLOWCONVEXHULL§算法——礼品包装算法
这些边的端点p和q都来自于P;另外,只要适当地定义由p和q所确定直线的方向,使得conv§总是位于其右侧,那么P中的所有点也都将落在该直线的右侧。反之亦然:如果相对于由p和q确定的直线,P\{p,q}中所有点都位于右侧,那么pq就是构成conv§的一条边。
#include <iostream>
#include <vector>
#include <algorithm>
struct Point {
int x, y;
bool operator==(const Point& other) const {
return x == other.x && y == other.y;
}
};
// 计算叉积 (P2 - P0) x (P1 - P0)
// 给定三个点 P0(x0,y0)、P1(x1,y1) 和 P2(x2,y2),叉积 (P1−P0)×(P2−P0) 可以判断点P2在直线 P0P1的哪一侧:
//如果结果为正,P2 在直线的左侧。
//如果结果为负,P2 在直线的右侧。
//如果结果为零,P2 在直线上。
int crossProduct(const Point& P0, const Point& P1, const Point& P2) {
return (P1.x - P0.x) * (P2.y - P0.y) - (P2.x - P0.x) * (P1.y - P0.y);
}
// 计算凸包的函数
std::vector<Point> slowConvexHull(std::vector<Point>& points) {
int n = points.size();
if (n < 3) return points; // 如果点数小于3,直接返回
std::vector<Point> hull;
// 找到最左边的点
int leftmost = 0;
for (int i = 1; i < n; i++) {
if (points[i].x < points[leftmost].x) {
leftmost = i;
}
}
int p = leftmost, q;
do {
hull.push_back(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++) {
// 如果点 i 在 p 和 q 的左侧,则更新 q
if (crossProduct(points[p], points[i], points[q]) < 0) {
q = i;
}
}
p = q;
} while (p != leftmost); // 直到回到起点
return hull;
}
int main() {
std::vector<Point> points = {
{0, 3}, {2, 2}, {1, 1}, {2, 1},
{3, 0}, {0, 0}, {3, 3}
};
std::vector<Point> convexHull = slowConvexHull(points);
std::cout << "Convex Hull Points:\n";
for (const auto& p : convexHull) {
std::cout << "(" << p.x << ", " << p.y << ")\n";
}
return 0;
}
上面的算法涉及一个假定:只要给定一条(有向)直线,以及另外一个点,那么无论这个点是位于直线的左侧还是右侧,总是能够准确地做出判断。然而,这个假设并不见得一定成立——如果各点的坐标都表示为浮点数,而且计算过程中所采用的也是浮点预算(floating point arithmetic),那么就必然存在舍入误差(rounding error),从而影响到测试精度。
试想有三个点p、q和r几乎共线,而其他各点与它们都相距很远。按照上面的算法,要分别对点(p,q)、(r,q)和(p,r)进行测试。既然这三个点几乎共线,则由于舍入误差的存在,判断的结果很有可能是:r位于直线pq的右侧,p位于直线rq的右侧,而q位于直线pr的右侧。显然,这种几何位置关系是不可能的——然而浮点运算可不管这些!在这种情况下,算法将会把这三条边全都挑选出来。
ConvexHull§算法——安德鲁单调链算法
为此将采用一种标准的算法设计模式——递增式策略——来设计一个递增式算法(incremental algorithm)。
递增式策略是一种算法设计模式,其核心思想是逐步构建问题的解。每次增加一个元素或一个步骤,并确保部分解在每一步都是正确的。这种策略通常用于解决可以逐步构建解的问题,例如凸包计算。
我们将逐一引入P中各点;每增加一个点,都要相应地更新目前的解。这个递增式方法将沿用几何上的习惯,按照由左到右的次序加入各点。因此,首先需要根据x坐标对所有点进行排序,产生一个有序的序列:p1,…,pn。
接下来,我们首先计算构成上凸包(upper hull)的那些顶点。所谓的上凸包,就是从最左端顶点p1出发,沿着凸包顺时针进行最右端顶点pn之间的那段。此后,再自右向左进行一次扫描,计算出凸包的剩余部分——下凸包(lower hull)。

若按照顺时针方向沿着多变形的边界行进,则在每个顶点处都要改变方向。若是任意的多边形,则每次的转向既可能是向左,也可能向右。然而,若是凸多边形,则必然每次都是向右转。根据这一点,在新引入pi之后,可以进行如下处理。
令Lupper为从左向右存放上凸包各顶点的一个列表。首先,将pi接在Lupper的最后——既然在目前已经加入的所有点中,pi是最靠右的,则它必然是(当前)上凸包的一个顶点,所以这样做无可厚非。然后,再检查Lupper中最末尾的三个点,看看它们是否构成一个右拐(right-turn)。若构成右拐,则大功告成,此时(更新后的)Lupper记录了组成上凸包的各个顶点p1,…,pi,接下来,就可以继续处理下一个点——pi+1。然而,若最后三个点构成一个左拐(left-turn),就必须将中间的(即倒数第二个)顶点从上凸包中剔除出去。
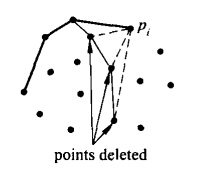
若出现这种情况,需要做的可能还远不止这些——因为,此时的最后三个点可能仍然构成一个左拐。果真如此,就必须再次将中间的顶点剔除掉。这一过程需要反复进行,直到位于最后的三个点构成一个右拐,或者仅剩下两个点。
#include <iostream>
#include <vector>
#include <algorithm>
struct Point {
int x, y;
// 重载小于运算符,用于排序
bool operator<(const Point& other) const {
return (x < other.x) || (x == other.x && y < other.y);
}
// 重载相等运算符
bool operator==(const Point& other) const {
return x == other.x && y == other.y;
}
};
// 计算叉积 (P2 - P0) x (P1 - P0)
int crossProduct(const Point& P0, const Point& P1, const Point& P2) {
return (P1.x - P0.x) * (P2.y - P0.y) - (P2.x - P0.x) * (P1.y - P0.y);
}
// 计算凸包的函数
std::vector<Point> convexHull(std::vector<Point>& points) {
int n = points.size();
if (n <= 3) return points; // 如果点数小于等于3,直接返回
// 按 x 坐标排序,如果 x 相同则按 y 排序
std::sort(points.begin(), points.end());
// 初始化凸包
std::vector<Point> hull;
hull.reserve(2 * n); // 预留空间
// 构建下凸包
for (int i = 0; i < n; i++) {
while (hull.size() >= 2 && crossProduct(hull[hull.size() - 2], hull.back(), points[i]) <= 0) {
hull.pop_back(); // 删除不满足条件的点
}
hull.push_back(points[i]);
}
// 构建上凸包
int lowerHullSize = hull.size(); // 下凸包的大小
for (int i = n - 2; i >= 0; i--) {
while (hull.size() > lowerHullSize && crossProduct(hull[hull.size() - 2], hull.back(), points[i]) <= 0) {
hull.pop_back(); // 删除不满足条件的点
}
hull.push_back(points[i]);
}
// 删除最后一个重复的点(起点)
hull.pop_back();
return hull;
}
int main() {
std::vector<Point> points = {
{0, 3}, {2, 2}, {1, 1}, {2, 1},
{3, 0}, {0, 0}, {3, 3}
};
std::vector<Point> convexHullPoints = convexHull(points);
std::cout << "Convex Hull Points:\n";
for (const auto& p : convexHullPoints) {
std::cout << "(" << p.x << ", " << p.y << ")\n";
}
return 0;
}
构建下凸包
下凸包是从左到右扫描点集,逐步构建凸包的下半部分。
算法步骤:
- 初始化一个空栈(或向量)
hull,用于存储凸包的点。- 从左到右遍历排序后的点集。
- 对于每个点,检查它是否在凸包的“内侧”:
- 如果当前点与栈顶两个点的叉积 小于等于 0,说明当前点在栈顶两个点的内侧(或共线),需要将栈顶的点弹出。
- 重复这个过程,直到当前点满足凸包的条件。
- 将当前点压入栈中。
构建上凸包
上凸包是从右到左扫描点集,逐步构建凸包的上半部分。
算法步骤:
- 从右到左遍历排序后的点集。
- 对于每个点,检查它是否在凸包的“内侧”:
- 如果当前点与栈顶两个点的叉积 小于等于 0,说明当前点在栈顶两个点的内侧(或共线),需要将栈顶的点弹出。
- 重复这个过程,直到当前点满足凸包的条件。
- 将当前点压入栈中。
如果由于采用浮点运算而出现舍入误差,原本应该属于凸包的某个点,就有可能被遗漏掉。不过,该算法输出的结构完整性还不至于收到破坏——也就是说,它依然能够计算出一个封闭的多边形链。无论如何,算法所输出的顶点列表,总是可以被理解为某个多边形各顶点沿顺时针的一个枚举;而且,前后相邻的任何三个点都构成一个右拐(或者,由于存在舍入误差,它们近似地构成一种问题)。另外,P中的每个点都不可能与计算出的凸包相距太远。
现在,只可能出现一种问题——当某三个点相距很近时,尽管它们构成一个很明显的左拐,却可能会被判断为一个右拐。其后果是,计算出的多边形上可能会出现一处凹陷。解决该问题的一种方法,就是要(比如,借助舍入误差)确保相距极近的输入点都能被当成同一个点来处理。
定理1.1
给定包含n个点的任意一个平面点集,其凸包都可以在O(nlogn)时间内构造出来。
证明
证明的方法是对处理的点数进行归纳。在for循环开始之前,Lupper只包含p1和p2两个点,这是平凡的情况,因为{p1,p2}的上凸包就是由这两个点自己确定的。假定Lupper中已经存放了{p1,…,pi-1}对应的上凸包,现在来考虑加入pi。
在执行完while循环之后,由归纳假设可知:Lupper(中的各点依次)组成一条链,而且该链始终都是右拐。此外,该链起始于{p1,…,pi}中字典序最小的点,终止于字典序最大的点——也就是pi。
为了证明Lupper中存放的点就是正确的结界,只需证明:{p1,…,pi}中的各点,要么在Lupper中,要么就位于该链的下方。
我们做归纳假设:在引入pi之前,没有任何点位于此前多边形链的上方。由于此前那条链必定位于新链的下方,故倘若有某个点位于新链的上方,它只可能出现由pi-1和pi界定的垂直条形区域中(如图1-15所示)。然而,这是不可能的——因为,果真如此,该点的字典序必然介于pi-1与pi之间(你需要按照类似的思路自行验证一下,在pi-1、pi或者其他点的x坐标相同时,这个结论依然成立)。
为了证明其时间复杂度的上界(upper bound),请首先注意到,按照字典序对各点进行排序,需要O(nlogn)时间。接下来,考虑上凸包的计算。for循环要执行的趟数是线性的。这样,只需要考虑其中while循环的执行趟数。在每一趟for循环中,while循环至少要执行一趟。而如果还要额外地执行while循环,则每趟都会将某个点从凸包中剔除出去。
在构造上凸包的整个过程中,每个点至多只能被删除一次,因此,在所有for循环中(while循环)额外的执行趟数加起来不会超过n。可以类似地证明,下凸包的计算也至多消耗O(n)时间。因此,整个计算凸包算法的时间复杂度取决于排序那一步,即O(nlogn)。





















 3324
3324

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








