SCAPE: Shape Completion and Animation of People

推荐阅读
https://zhuanlan.zhihu.com/p/30683652

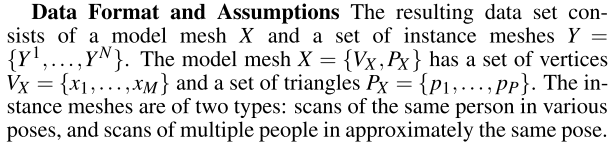
model mesh X 有M个点, P个三角形
N个instance meshes

4 Pose Deformation

公式(1), k为第几个三角形, j为每个三角形的第几个点, i是第i个instance模型
$Q_k^i$为匹配第i个instance模型 , 第k个三角形的形变

然后模型呢有很多rigid parts, 每个三角形属于某个特定的rigid part, 两个相信的rigid parts 之间会有一个Joint

$l[k]$为跟第k个三角形所属的rigid part
$R_{l[k]}^i$, 第k个三角形所属的rigid part的rigid形变.

公式(2), 给定形变,然后以每个三角形的第一点作为原点来计算最终的y

4.2 相邻两个rigid parts产生一个joint, 这个joint的相对形变就为 $R_{l_1}^T{R}_{l_2}$
后面$t,\theta$是从rotation matrix到twist的转换公式

$Q_k^i={\mathcal{Q}}_{{\mathbf{a}}_k}(△r_{l[k]}^i)$
输入是每个三角形最近两个joints的形变, 输出就是该三角形的形变$Q_k$
怎么转换呢?
需要中间变量 ${\mathbf{a}}_k$, 我们将$$\left[\begin{array}{c}△r_{l[k]}^i\\ 1\end{array}\right]$$通过$7\times 9$的矩阵转换到$Q$的9个元素
当已知$Q$的时候,我们就可以将$7\times 9$的矩阵(${\mathbf{a}}_k$)通过公式(4)训练出来,

但是$Q$是不知道的, 要怎么去算呢? 可以通过公式(5), 注意$l_{k_1}=l_{k_2}$表示相邻的两个rigid parts是属于同一个rigid parts

5 Body-Shape Deformation

跟Pose deformation的思想一样, 还是要训练一组中间变量

输入是the mesh-specific coefficients ${\beta }^i$, 输出是$S^i$, 注意每个三角形都一个$S_k^i$

过程跟4差不多, 先是通过公式(8), 算出$S_k^i$, 这样就得到了$S^i$, 然后建立一个${\beta }^i$到$S_k^i$的全链接, 链接线上的参数也就是这里的$U,\mu$

公式(9), 类似于公式(2), 给定一组形变, 然后算出最终模型点的位置

6 Shape completion

公式(10), 第二部分作了匹配点上的约束, 将匹配硬拉过来, 同时用第一部分来实现前面的形变约束. 具体迭代这里就不细讲了

7,8 也不讲了