基于Spark的交通流预测控制

基于Spark云的并行计算用于交通网络流量预测控制的非解析预测模型

摘要

在物联网（IoT）背景下处理交通大数据时，单机计算环境下的交通控制难以适应大规模、快速的分析与决策需求。为解决这一问题，本文提出一种基于模型预测控制（MPC）机制的交通网络流量控制并行计算方法。构建了一种基于非解析规则的交通流模型，利用交通流的实时反馈信息预测预测时域内的车辆行驶情况，并评估候选控制策略的性能。此外，为了加速求解预测时域内最优控制方案的过程，设计了一种基于Spark云计算的两级分层并行遗传算法（HPGA）。通过并行计算架构，借助弹性分布式数据集（RDD）将计算密集型优化任务分解为多个并行子任务，从而提高计算效率。仿真结果表明，所提出的方法在非饱和与过饱和交通场景下对交通网络流量预测控制具有有效性。基于Spark的并行优化方法在处理交通网络流量控制的大数据时，具备满足在线优化计算需求的能力，同时保持良好的控制性能。

索引术语 —交通网络流，模型预测控制（MPC），Spark云计算，非解析预测模型，分层并行遗传算法。

一、引言

随着信息通信技术和物联网（IoT）的快速发展，智能交通系统（ITS）已进入由大数据驱动的新发展阶段。各类交通传感器采集多源交通流数据，这些采集的数据为提升交通管理水平提供了丰富的交通信息。然而，如何快速处理如此庞大的数据以获得理想的控制策略仍然是一个挑战。Apache Spark [1], 作为一种新一代云计算模型，已应用于疾病诊断 [2], 台风模拟 [3], 大数据时间序列预测 [4], 等领域。这得益于Spark云在基于内存的计算架构方面的优势。本文尝试提出一种基于Spark云的并行计算实施方案，用于交通网络流量预测控制，以解决采用非解析预测模型时面临的大数据处理和复杂迭代优化问题。

以往的交通控制策略大致分为两类：固定时间交通控制（FTC）和交通响应控制（TRC）[5]。FTC方案的信号参数利用低采样率的GPS轨迹进行估计，以引导驾驶行为[6]。在FTC控制方法[7],[8],中，信号交叉口的控制方案通过历史交通流量数据离线确定，因此信号配时参数无法自动调整以应对交通状况的不确定性和干扰。而TRC方法[9]–[13]恰好弥补了这一局限性，利用实时测量在线调整最优信号设置。基于此，利用博弈论协同优化孤立交叉口的信号配时和车辆重新路径规划，以缓解交通拥堵[14]。提出了最大压力控制方法，利用相邻路段的饱和流量和排队长度差异来调整相位持续时间[15]。为了降低计算复杂度，应用广义比例分配方法仅需进口车道的排队长度即可控制相位激活[16]。此外，提出了一种基于多源数据的自适应切换信号控制方法，以提高对联网车辆的控制效果[17]。进一步地，开发了一种加权分布控制策略，以平衡路网中局部道路之间的拥堵消散[18]。由于缺乏交通流预测，当前控制方案对未来交通状况的潜在影响未被明确考虑。

模型预测控制（MPC）[19],[20]可以通过考虑候选控制方案对未来交通状态的影响来确定当前最优的控制决策。基于MPC的交通控制器利用模型来预测未来交通动态并计算潜在的控制性能。在每个控制周期，仅将优化后的控制序列的第一个元素应用于实际交通系统。随后，预测时域向前滚动一个周期，并根据反馈的交通状态和预测模型重复进行优化过程。MPC方法被提出用于协调高速公路交通中的匝道计量和可变速度限制[21]。该MPC方法还被提议用于优化自动化公路系统中入口匝道处的车速限制、车道分配以及车队的放行时间[22]。滚动时域策略被用于解决多出行者路径选择问题[23]。边界控制与路线引导作为经济型模型预测控制相结合，以提升城市路网中的交通流动性[24]。此外，针对城市道路和高速公路网络引入了宏观交通流和排放模型，在模型预测控制框架内减少交通拥堵和排放[25]–[27]。然而，为将模型预测控制策略应用于实际交通工程，优化控制目标所需时间的减少仍值得进一步研究。

为进一步减少在线优化的时间消耗，将整体路网划分为小型子网络以加速求解过程[28]–[30]。在后退时域框架下，对宏观预测模型进行简化和参数化，以降低在线计算时间[31]–[33]。此外，开发了混合整数线性规划、基于梯度的优化和二次规划等快速优化方法，以提高基于改进宏观交通流模型的城市交通网络中模型预测控制的实时可行性[34],[35]。宏观交通流模型（如METANET模型、S模型、储存‐转发模型及其简化形式）能够粗略地描述交通密度、交通量和占有率等宏观交通现象。而非解析微观交通流预测模型则擅长直接描述交通流的交互行为和动态分布，有利于充分实现模型预测控制策略的优势。同时，将单机计算环境扩展至云计算平台，有助于满足车联网（IoV）快速发展步伐所带来的计算需求，其中需要对车辆运动进行逐一建模。

本文尝试提出一种新的交通网络流预测控制方法，该方法结合了非解析微观交通流预测模型以及部署在Spark云上的相应在线并行非解析优化方法。基于规则的非解析车辆运动模型被用于描述个体及交互式驾驶行为的细节，并根据交通流的反馈信息和预设信号控制方案来预测未来交通状态。为了缓解在预测时域内求解全路网最优控制策略所带来的巨大计算负担，设计并实现了基于Spark云的两级分层并行遗传算法（HPGA）。与现有方法相比，所设计的混合并行遗传算法（HPGA）基于近年来开发的Spark云计算平台的主从式和基于内存的计算架构。此外，考虑到遗传算法求解过程中各个阶段计算负载分布不均的特点，对遗传算法进行了并行化处理。其中，染色体适应度评估的计算负载显著较大，涉及交通网络流预测，因此将染色体在多个从节点上进行评估，作为候选控制动作的一级并行性。接着，主节点采用精英策略进行全局选择，以确保局部进化实现全局收敛。随后，二级并行性聚焦于交叉与变异操作，通过将多个子种群分配到从节点来枚举可行控制方案。所设计的混合并行遗传算法（HPGA）充分考虑了计算平台和求解问题的特性。

本文其余部分组织如下。第二节建立了非解析微观交通网络流预测模型。基于此，第三节介绍了交通网络流量预测控制的MPC优化问题、并行计算方法及基于Spark云的实施方案。第四节展示了所提出的交通网络流量预测控制及其对应的并行优化方法的控制性能和时间有效性。最后，在第五节中概述了结论和未来工作。

第二章 非解析微观交通网络流预测模型

A. 时空约束

在城市道路网中的车辆行驶受到沿行驶路线复杂的速度和位置限制，如图1所示。

1) 速度限制 ：车辆速度受道路状况、交通信号状态、天气条件等因素制约。
- (1) 最高速度限制：驾驶过程中允许的最大速度由道路基础设施和驾驶设备决定。
- (2) 区域相关速度限制：当车辆接近特定区域（如医院、学校、信号交叉口等）时，应适当减速。
- (3) 临时限速：在道路损坏、体育赛事、极端天气、交通事故等情况发生时，需要设置临时速度限制以提示驾驶员减速。

上述三种速度限制的最小值定义为vlim(x)，其中x为车辆位置。vlim(x)将道路动态划分为一系列具有不同速度限制的路段。

算法1 ：后随车辆速度更新规则
当前速度 vn(t)，位置 xn(t) 和距离 d(t)。
预测速度 vn(t+ 1)。

1: IF d(t) ≥ dmax(t)
2:    vn(t + 1) = 最小值(vn(t) + amax, vlim(xn(t)), 两相邻车辆之间的距离)
3: 否则 IF dmin(t) ≤ d(t) < dmax(t)
4:    vn(t + 1) = 最小值(最大值(vn(t) + af, 0), vlim(xn(t)), d(t))
5: 否则
6:    vn(t + 1) = 最小值(最大值(vn(t) − bmax, 0), vlim(xn(t)), d(t))
7: 结束如果

2) 位置约束 ：根据驾驶行为特征，道路交通网络中的车辆可分为跟随车辆和领头车辆。

后随车辆的驾驶行为受两辆相邻车辆之间距离 d(t) 的影响，该距离通过以下方式计算

$$
d(t) = x_{n’}(t) - x_n(t) - l_v - SM \tag{1}
$$

其中 $x_n(t)$ 和 $x_{n’}(t)$ 分别表示在时刻t，两辆相邻车辆n和n’从道路段起点起算的位置，$l_v$ 为车辆长度，SM为车辆停止所需的安全余量。

领头车辆的驾驶策略受前方相邻信号交叉口以及下一路段（路段）上尾部车辆的影响。当当前领头车辆在前方交叉口遇到绿灯，且下一路段上至少存在一辆车辆时，该车辆将被视为后随车辆，但(1)应进行修正为

$$
d(t) = x_{\text{next tail}}(t) + l_r - x_n(t) - l_v - SM \tag{2}
$$

其中 $x_{\text{next tail}}(t)$ 为从下一路段起点出发的尾部车辆的位置，$l_r$ 为当前路段的长度。当当前前导车辆在前方信号交叉口遇到红灯时，该前导车辆也将被视为跟车，但式(2)应重写如下:

$$
d(t) = x_s(t) - x_n(t) \tag{3}
$$

其中 $x_s(t)$ 为前一个信号交叉口或目的地的位置。当前导车辆在前方信号交叉口遇到绿灯、尚未到达目的地，且下一条进入道路无车辆时，前导车辆的驾驶行为仅受速度限制的影响。

B. 车辆运动模型

1) 速度与位置更新规则 ：在本节中，我们采用元胞自动机对交通流[40],进行描述，其中速度和加速度在时间单位内被量化，并且不同物理变量之间的计算以忽略时间单位的数值方式进行。本节使用的一些重要符号如下所列。

算法2：前导车辆的速度更新规则
案例：无法等同于后随车辆
当前速度 vn(t) 和位置 xn(t)。
预测速度 vn(t+ 1)。

1: 如果 vn(t) < vlim(xn(t))
2:    vn(t + 1) = 最小值(vn(t) + amax, vlim(xn(t)))
3: 否则如果 vn(t) = vlim(xn(t))
4:    vn(t + 1) = vn(t)
5: 否则
6:    vn(t + 1) = 最小值(最大值(vn(t) − bmax, 0), vlim(xn(t)))
7: 结束如果

• amax：驾驶员可采用的最大加速度。
• bmax：驾驶员可采用的最大减速度。
• bmin：驾驶员可采用的最小减速度。
• af：与两辆相邻车辆距离相关的跟车（CF）加速度。
• vn(t)：车辆 n 在当前时刻 t 的当前速度。
• dmax(t)：当驾驶员采用bmin时，车辆相对于前一辆相邻车辆的最大制动参考距离。理论值为 $d_{\text{max}}(t) = \frac{v_a(t)^2}{2b_{\text{min}}} + v_a(t)$，其中 $v_a(t) = \min(v_n(t) + a_{\text{max}}, v_{\text{lim}}(x_n(t)))$。
• dmin(t)：当驾驶员采用bmax时，车辆相对于前车的最小制动参考距离。其理论值为 $d_{\text{min}}(t) = \frac{v_b(t)^2}{2b_{\text{max}}} + v_b(t)$，其中 $v_b(t) = \max(v_n(t) − b_{\text{max}}, 0)$。

根据跟车模型，加速度 af 的计算如下:

$$
a_f = \kappa[V(d_h(t)) - v_n(t)] + \lambda \mathcal{H}(−Δv(t)) Δv(t) \tag{4}
$$

with

$$
V(d_h(t)) = \frac{v_{\text{max}}}{2} [\tanh(d_h(t) - SM) + \tanh(SM)] \tag{5}
$$

其中，V(·) 是最优速度函数， $\mathcal{H}(·)$ 是海维赛德函数，$Δv(t)$ 是车辆 n 与 n’ 的速度差， $\kappa$ 是驾驶员的敏感度， $\lambda$ 是灵敏度系数，$d_h(t)$ 是两辆相邻车辆的车头间距，计算公式为 $d_h(t) = x_{n’}(t)−x_n(t)−l_v$。

后随车辆的速度更新规则在算法1中进行了总结，主要包括三种情况：自由加速、跟车和紧急制动。在算法1中，第1行和第2行表示自由加速情况，即当amax且d(t) ≥ dmax(t)时，后随车辆以最大加速度执行加速行驶策略，直到达到最大允许速度。当两辆相邻车辆之间的距离满足dmin(t) ≤ d(t)< dmax(t)时，采用af来引导跟车过程中的加速或减速行为。

目的，如跟车案例中第3行和第4行所述。第5行和第6行描述了紧急制动情况：当后随车辆检测到d(t)< dmin(t)时，将采用最大减速度bmax的紧急减速策略以确保安全。在该模型中，自由加速、适度加减速以及紧急制动均被建模，这些行为通常出现在实际驾驶行为中。

如果前导车辆满足由(2)和(3)描述的条件，则前导车辆的速度更新规则等同于算法1中所示的规则。否则，前导车辆的速度更新规则按算法2中总结的方式执行。在算法2中，前导车辆仅需判断当前速度vn(t)是否超过最大允许速度。如果vn(t) < vlim(xn(t))，则前导车辆的速度可加速至vlim(xn(t))，如第1行和第2行所述。但如果vn(t) = vlim(xn(t))，前导车辆将在下一时刻t + 1保持当前速度，如第3行和第4行所示。相应地，如第5行和第6行所示，若vn(t) > vlim(xn(t))，前导车辆将减速。

前导车辆和后随车辆的位置更新规则如图所示

$$
x_n(t+ 1) = x_n(t) + v_n(t). \tag{6}
$$

2) 驾驶路线选择行为 ：在车联网环境下，车辆可通过卫星导航系统和无线通信基站实时获取道路上的交通量信息，如图2所示。本文中，车辆的行驶路线采用动态最短路径，该路径随时间变化，并与可变的交通流相关。从第i个交叉口到相邻的第i′个交叉口的路段在时刻t的行驶时间被估计为该路段的权重wi,i′(t)，其计算方式如下

$$
w_{i,i’}(t) = \frac{l_{i,i’}}{[v^{\text{max}} {i,i’}(1 - \rho {i,i’}(t)/\rho^{\text{j am}}_{i,i’})]} \tag{7}
$$

其中 $l_{i,i’}$、$v^{\text{max}} {i,i’}$、$\rho {i,i’}(t)$ 和 $\rho^{\text{j am}}_{i,i’}$ 分别为从第i个交叉口到第i’个交叉口的路段长度、最大速度、瞬时密度和拥堵密度。

因此，车辆的动态最短路径由候选路径中路段权重之和最小的那些路段组成。

图2展示了一个车辆路线动态变化的示例。红色虚线箭头表示原始行驶路线。一辆车感知到路段上的交通流发生了显著变化，通过使用(7)计算路段权重重新规划行驶路线。车辆的路线变化由图2中的蓝色箭头表示。

III. 基于Spark云计算的模型预测控制

A. 模型预测控制问题描述

基于模型预测控制的交通网络流控制是将控制问题转化为滚动时域内的基于模型的在线优化问题。它主要包括三个部分：交通流预测、目标函数优化和滚动时域方案。

1) 交通流预测 ：在每个优化或控制步长中，采用第二所述的车辆运动模型来预测未来交通动态，并评估城市道路网的潜在控制策略。该模型以综合方式描述了驾驶行为多样性，如跟车、自由加速和紧急制动，以及时空约束对驾驶行为的影响。通常情况下，交通流模型越精细，所预测的交通动态与实际情况越一致。因此，通过模型预测控制中的预测模型获得的控制策略更有可能实现交通网络流的预期控制性能。

2) 目标函数优化 ：为了提高城市道路网的通行能力，模型预测控制在预测时域Np内的优化目标函数被表述为:

$$
\max \hat{J}(\hat{s}(k_c), \hat{u}(k_c)) = \sum_{i=1}^{Q} \sum_{k=k_c}^{k_c+N_p -1} M_i(k+ 1) \tag{8}
$$

s.t.

$$
g^{\text{min}} i \leq g {i,j,k} \leq g^{\text{max}}_i \tag{9}
$$

$$
\sum_{j=1}^{N_i} g_{i,j,k} = C_i - L_i \tag{10}
$$

$$
0 \leq \theta_{i,k} \leq C_i - L_i \tag{11}
$$

$$
O_i \in {ph_{i,j} | j= 1, 2,\cdots, N_i} \tag{12}
$$

其中，$k_c$ 为当前控制步， $\hat{s}(k_c)$ 表示预测交通状态，如车辆的预测位置和速度， $\hat{u}(k_c)$ 表示预测控制输入序列，如绿灯时间和相位差。$M_i(k + 1)$ 表示在时刻k+ 1通过第i个信号交叉口的车辆数量，$N_p$ 为预测时域长度，$Q$ 为整体路网中的信号交叉口数量。$g_{i,j,k}$ 表示第i个交叉口在时刻k第j相位的绿灯时间，$g^{\text{min}} i$ 和 $g^{\text{max}}_i$ 分别为绿灯时间$g {i,j,k}$的上下界。$C_i$ 为信号周期长度，$L_i$ 为固定损失时间，$N_i$ 为与第i个交叉口相关的相位数。$\theta_{i,k}$ 表示第i个交叉口在时刻k的信号相位偏移。$O_i$ 为第i个交叉口的相位序列集合，$ph_{i,j}$ 表示第i个交叉口的第j相位。

3) 滚动时域方案 ：预测时域内的未来交通状态 $\hat{s}(k_c)$ 和控制输入 $\hat{u}(k_c)$ 分别表示为

$$
\hat{s}(k_c)=[s(k_c+ 1|k_c), s(k_c+ 2|k_c),\cdots, s(k_c+ N_p |k_c)] \tag{13}
$$

$$
\hat{u}(k_c)=[u(k_c|k_c), u(k_c+ 1|k_c),\cdots, u(k_c+ N_p −1|k_c)]. \tag{14}
$$

为了减少需要优化的控制变量数量，定义了控制时域 $N_c(N_c< N_p)$，使得

$$
\hat{u}(k_c+ k|k_c)= \hat{u}(k_c+ N_c −1|k_c), k= N_c,\cdots, N_p −1. \tag{15}
$$

也就是说，(14) 中的控制变量可以重写为

$$
\hat{u}(k_c)=[u(k_c|k_c), u(k_c+ 1|k_c),\cdots, u(k_c+ N_c −1|k_c)]. \tag{16}
$$

一旦根据(8)对控制输入序列 $\hat{u}(k_c)$ 进行了优化，仅该序列中的第一个元素，即 $u^* (k_c|k_c)$，将在控制步长 $k_c$ 处实施到实际交通流系统中。此时，预测模型将接收新检测到的交通状态作为初始状态进行预测。因此，整个预测时域向前移动一步，并在新的预测时域内重新启动相同的优化过程。

B. 基于Spark的并行优化方法

1) 并行算法设计的动机 ：为了解决使用所开发的非解析预测模型表示的具有多重约束的非线性优化问题（如(8)‐(12)所示），应设计一种适当的方法来应对大量计算负载，并实现优异的控制性能和计算效率。

遗传算法作为智能优化算法的一员，在处理非解析优化问题时具有优异的全局收敛能力。然而，对于交通网络流量控制中的大规模优化问题，需突破传统串行遗传算法在单机环境下的限制。近年来流行的Spark云计算技术正适用于解决复杂的海量数据迭代优化问题。因此，设计了一种基于Spark云计算的两层分级并行遗传算法（HPGA），以加速在预测时域内求解最优控制决策的优化过程。

2) 两级分层并行遗传算法 ：通用遗传算法主要由适应度计算、选择、交叉和变异组成。某些计算阶段可根据计算负载的分布以并行方式进行。我们构建了两层分级并行性。第一级是将大规模种群分配到Spark云上的不同计算节点，并同步执行计算密集型适应度评估任务，以应对全路网交通流仿真预测。第二级并行性则是针对各染色体进行交叉和变异操作，尽管这些操作涉及的计算负载相对较大，但仍将其部署到多个从计算节点以处理可行解生成。然而，选择操作在主节点上执行，该过程计算负载较小，通过收集来自从节点的局部计算结果来实现优胜劣汰。所有从节点均可与主节点建立信息共享通道。整体结构的

图3展示了在Spark云上实现的混合并行遗传算法（HPGA）。控制输入参数，例如预测时域Np内所有信号交叉口的信号偏移和绿灯时间，被编码为一条染色体，表示针对由(8)‐(12)描述的问题的一个可行解。随机生成的多条染色体构成种群代，提供一个可行解集。

如图3所示，基于构建的种群，混合并行遗传算法（HPGA）的进化过程大致分为三个阶段。在第一阶段，种群以细粒度方式被划分为不同的弹性分布式数据集（RDD）作为子种群，并分配给Spark集群中的执行器。执行器利用预测模型根据公式(8)计算适应度值，并将<染色体, 适应度>键值对返回至驱动节点。在第二阶段，针对收集到的<染色体, 适应度>对，在驱动节点上采用轮盘赌方法进行全局选择，其原则是：适应度越高，染色体的被选概率越大。随后，种群以粗粒度方式分解为若干子种群，并分配给不同的执行器。在第三阶段，执行器对子种群执行交叉与变异操作，获得的新一代种群作为下一次迭代过程的父代种群。若满足终止条件，则输出表示当前最优控制决策序列的最佳染色体；否则，算法返回第一阶段继续新的迭代计算过程。在第一和第三阶段，并行执行的适应度评估以及交叉与变异操作减少了算法的求解时间；而在第二阶段，串行选择操作确保了从局部并行进化中实现全局收敛。

图3的详细描述总结在算法3中。第1‐2行说明了对交通网络流的当前状态进行采样并初始化参数。第3行表示编码染色体并构建初始种群。第4行表示将种群划分为若干子种群，并将其分发到不同的执行器。第5‐19行展示了在相应执行器上利用开发的预测模型以并行方式执行适应度评估。其中，第9‐11行表示在预测时域k时刻Np进行交通流预测仿真；第12‐15行描述了统计通过各个交叉口的车辆数量，并在预测时域k时刻Np更新信号交叉口的状态；第17行表示在预测时域Np的预测完成后，根据各染色体的目标函数为其分配适应度值。第20行反映了在驱动节点上使用轮盘赌方法进行全局选择操作。第21‐25行描述了并行交叉和变异过程以生成新子种群。第26‐28行表明新种群被重新分解为下一次迭代的父代种群。当满足终止条件时，将输出代表当前最优控制序列的最佳染色体，如第29行所示。

算法3中的计算时间主要由染色体初始化、适应度评估、选择、交叉与变异操作的时间组成。这些时间均与NgenNch成正比。适应度评估需要在预测时域内基于预设信号控制方案进行交通流仿真预测，该部分的计算时间与Np Nveh/Ne1成正比，其中Nveh表示道路网络中运行的车辆数量。对于交叉与变异操作，其计算时间随着执行器数量Ne2的增加而相应减少。因此，并行算法3的时间复杂度表示为

$$
T_p = O_p[N_{\text{gen}}N_{\text{ch}}(2+ N_p N_{\text{veh}}/N_{e1}+ 2/N_{e2})] ≈ O_p(N_{\text{gen}}N_{\text{ch}} N_p N_{\text{veh}}/N_{e1}). \tag{17}
$$

公式(17)表明，适应度评估的计算时间远大于染色体初始化、选择、交叉和变异的计算时间。

C. 基于Spark的交通网络流预测控制

如图4所示，模型预测控制器部署在Spark云计算中心，从全局视角协调局部信号交叉口的交通网络流。在车联网环境下，交通仿真系统与云计算中心之间建立了双向信息交换通道。通过多源传感器采集交通网络状态（如车辆速度、位置及信号交叉口状态），并经由无线基站上传至云控制中心。利用非解析微观预测模型，根据交通状态反馈信息计算各候选控制方案的控制性能。在此基础上，采用混合并行遗传算法（HPGA）加速带约束目标函数的求解过程，并通过Spark云计算平台的多节点多核计算资源输出最优控制序列。仅将优化后的控制序列的第一个元素通过构建的信息交换通道执行于实际交叉口。上述过程随着预测时域的滚动重复进行，以实现对交通网络流的调节。

基于Spark云的并行计算用于交通网络流量预测控制的非解析预测模型

四、仿真实验

A. 仿真网络与参数配置

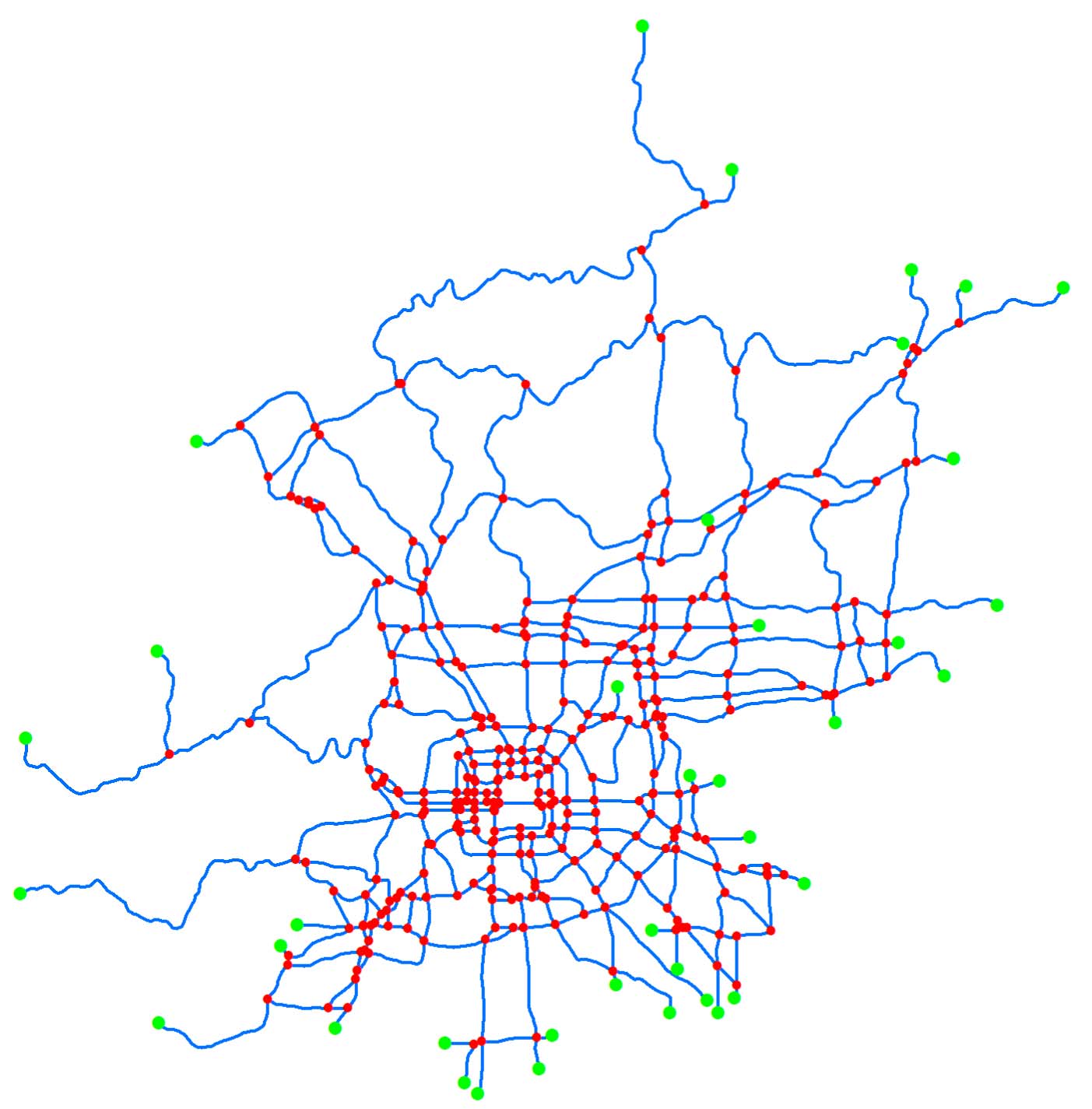
为了验证所开发的交通网络流量预测控制方法的性能，采用了北京市的道路网络。如图5所示，该网络包含317个信号交叉口（用数字1至317表示，地图中的红点）和38个无信号交叉口（用数字318至355表示，地图中的绿点），以及539条道路链接（用数字1至539表示），其中仿真场景中的干线道路设置为双向，包含四车道，所有交叉口的信号均设置为四相位。

仿真实验的主要参数配置为：信号周期 $C_i = 180$s，信号损失时间 $L_i = 12$s，最小绿灯时间 $g^{\text{min}} i = 12$s，最大绿灯时间 $g^{\text{max}}_i = 132$s；交叉概率 $p_c = 0.9$，变异概率 $p_m = 0.1$，种群大小 $N {\text{pop}} = 63$，最大生成次数 $N_{\text{max}} = 20$；车辆长度 $l_v = 5$m，安全间距 $SM = 1$m；仿真周期 $t_s = 3$s，总仿真时间 $N_s = 5400$s；预测时域 $N_p = 2C_i$，控制时域 $N_c = 1C_i$。

仿真实验在大数据处理平台——阿里云弹性 MapReduce（EMR）[41]上实施。我们选择了位于北京的同一资源管理组中的64个计算节点作为实验云计算平台，每个计算节点配置了16GB内存和四核CPU。云计算能够灵活分配可扩展计算资源，如CPU、内存、磁盘和带宽，以满足不同规模道路网络的应用需求。操作系统为 CentOS 7.4，其上安装了Spark 2.4.2和YARN 2.8.5，分别负责大数据并行处理和资源调度。

B. 评估指标

第一个评估指标是在时刻 $k_c$ 对交通网络实施信号控制方案后，在一个公共周期内实际通过所有信号交叉口的总车辆数（TVP），其定义如下:

$$
TVP(k) = \sum_{i=1}^{Q} TVP_i(k) = \sum_{i=1}^{Q} \sum_{t=k}^{k+C} M_i(t) \tag{18}
$$

其中，$TVP_i(k)$ 表示在时刻 $k$ 之后的一个公共周期 $C$ 内实际通过第 $i$ 个交叉口的车辆数量。$M_i(t)$ 表示在时刻 $t$ 实际通过第 $i$ 个交叉口的车辆数量，而 $Q$ 为交叉口数量。

第二个评估指标是在某一时刻 $k_c$ 对交通网络实施信号控制方案后，在一个公共周期内通过所有信号交叉口的车辆的平均延误时间（ADT）。即车辆从前一个交叉口到已通过交叉口的实际行驶时间与自由流速度下的理想行驶时间之差，表示为

$$
ADT(k) = \sum_{i=1}^{Q} ADT_i(k) = \sum_{i=1}^{Q} \frac{\psi^{\text{act}}_i(k) - \psi^{\text{idea}}_i(k)}{N^{\text{vp}}_i(k)} \tag{19}
$$

其中，$ADT_i(k)$ 表示在时刻 $k$ 之后的一个公共周期 $C$ 内通过第 $i$ 个交叉口的车辆的平均延误时间。$N^{\text{vp}}_i(k)$ 表示在时刻 $k$ 之后的一个公共周期 $C$ 内通过第 $i$ 个交叉口的车辆数量。$\psi^{\text{act}}_i(k)$ 表示这些车辆从前一个交叉口到第 $i$ 个交叉口的实际行驶时间，而 $\psi^{\text{idea}}_i(k)$ 表示在时刻 $k$ 之后的一个公共周期 $C$ 内，这些车辆以允许的最大速度行驶的最短行驶时间。

交通流密度也被选为评估道路网络中拥堵分布的指标，其表达式为

$$
\rho_{i,i’}(k) = \frac{N^{\text{v}}_{i,i’}(k)}{N^{\text{L}}_r l_r} \tag{20}
$$

其中 $\rho_{i,i’}(k)$ 和 $N^{\text{v}}_{i,i’}(k)$ 分别表示在时刻 $k$ 从交叉口 $i$ 到相邻交叉口 $i’$ 的交通流密度和车辆数量。$N^{\text{L}}_r$ 和 $l_r$ 分别为车道数和道路长度。

加速比 $S_p$ 是在相同计算任务下评估计算效率的关键指标，其描述为

$$
S_p = T_s / T_p \tag{21}
$$

其中 $T_s$ 表示单机计算时间，$T_p$ 表示使用Spark云进行并行计算的计算时间。

C. 控制精度与通用性能力评价

本节中，选择单机MPC、FTC和TRC作为基于Spark云的MPC的对比对象，其中Spark云配置为64个节点（一个主节点和63个从节点）。对于TRC策略，在距交叉口200米处的路段设置一个车辆检测器。在该控制中，若未检测到交通流或已达到最大绿灯时间限制，则当前信号相位终止并切换至下一相位；否则，绿灯时间延长9秒。该方法利用当前时刻采集的交通状态进行控制决策，不进行预测推理，而所提出的方法则考虑了候选控制方案对未来交通动态的累积效应。

利用两种具有不同交通需求的典型交通场景来模拟实际道路交通状况。第一个交通场景对应轻度交通需求下的非饱和交通状态，而第二个交通场景模拟了重度交通需求下的过饱和交通状态。饱和度通常通过单位时间内通过路段某点的车辆数与设计通行能力限值之比来衡量。在这两种场景中，交叉口处单位时间内的车辆生成率被用来调节饱和度。

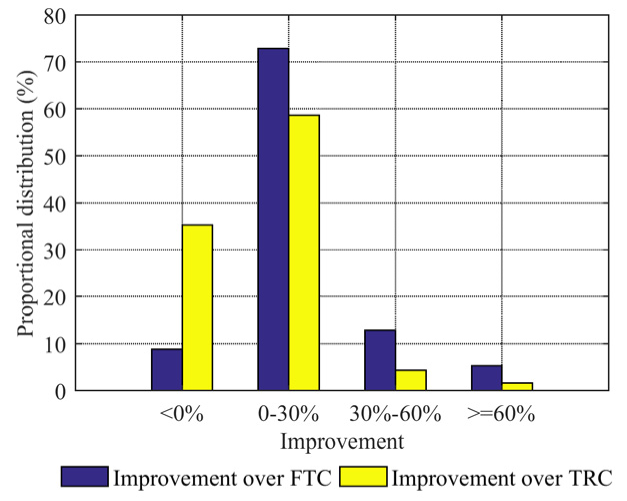
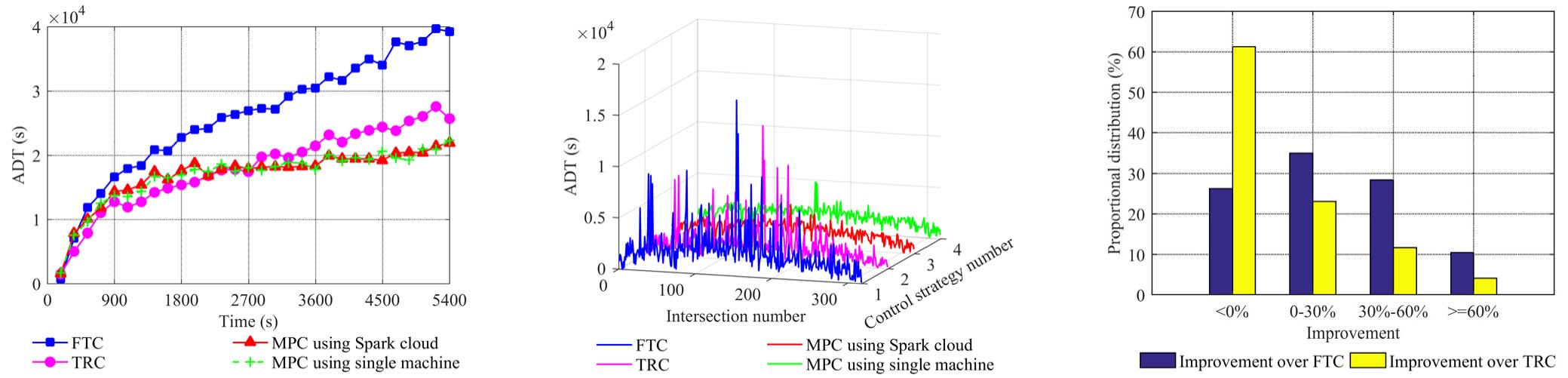
对于非饱和交通场景，如图6(a)和图7(a)所示，在仿真初期将交通网络流初始加载到道路网络时，三种控制器在总车辆通过量（TVP）和平均延误时间（ADT）指标上没有明显差异。但在仿真的大多数阶段，模型预测控制（MPC）、固定时序控制（FTC）和定时响应控制（TRC）方案之间的差异逐渐显现。如图6(b)和图6(c)所示，与FTC方案相比，采用MPC方法的TVP在72.87%的交叉口改善了0–30%，在12.93%的交叉口改善了30%–60%，在5.36%的交叉口改善超过60%。而对于TRC方法，与之相比，采用MPC方法的TVP在58.68%的交叉口改善了0–30%，在4.42%的交叉口改善了30%–60%，在1.58%的交叉口改善超过60%。与FTC方法相比，采用MPC方法的ADT在35.02%的交叉口改善了0–30%，在28.39%的交叉口改善了30%–60%，在10.41%的交叉口改善超过60%，如图7(c)所示。图7(a)表明，随着交通负荷的增加，MPC方案的ADT性能将优于TRC方法。在ADT方面，与TRC方法相比，MPC方案可在23.03%的交叉口改善0–30%，在11.67%的交叉口改善30%–60%，在4.1%的交叉口改善超过60%，如图7(a)所示。

图8表示交通流密度图像，其中红色区域表示拥堵，绿色区域表示畅通状态。显然，采用FTC和TRC方法控制的道路网络部分路段出现拥堵，而几乎所有采用MPC方法控制的路段均处于交通流畅通状态。

对于过饱和交通场景，图9和图10展示了与图6和图7类似的结果。图9(b)和(c)表明，采用模型预测控制的总车辆通过量与采用FTC方案相比，在61.51%的交叉口提升了0–30%，在11.04%的交叉口提升了30%–60%，在3.47%的交叉口提升了超过60%。与采用TRC方法相比，采用MPC方案的总车辆通过量（TVP）在61.51%的交叉口增加了0–30%，在11.04%的交叉口增加了30%–60%，在3.47%的交叉口增加了超过60%。图10(b)和(c)表明，与采用FTC方案相比，采用MPC方案的ADT在30.60%的交叉口减少了0–30%，在29.34%的交叉口减少了30%–60%，在16.72%的交叉口减少了超过60%。此外，就ADT指标而言，MPC与TRC方法相比，该方案在20.19%的交叉口性能提升0–30%，在15.14%的交叉口提升30%–60%，在8.83%的交叉口提升超过60%，如图10(c)所示。图8和图11显示，在过饱和状态下发生拥堵的路段数量高于未饱和状态。然而，采用MPC方案发生拥堵的路段数量仍显著少于FTC和TRC方案，这一点在图11中有所体现。

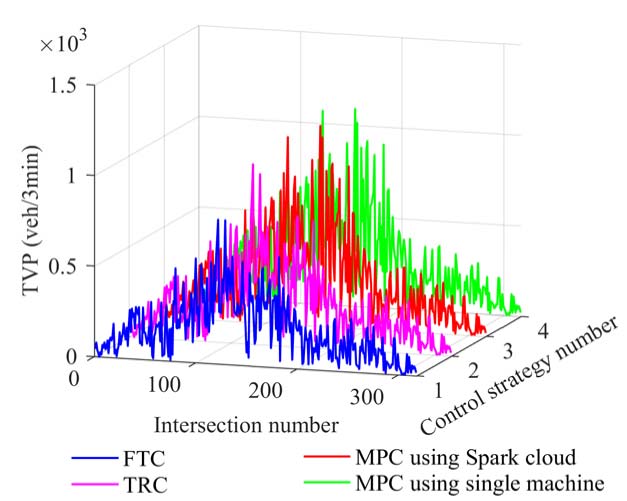
比较图6和图7与图9和图10，不难发现过饱和交通场景下总车辆通过量和平均延误时间的改善程度高于非饱和交通场景下的改善程度。这是因为在交通流量相对较大时，采用滚动时域方法的MPC方案从全局视角调节交通通行量和延误的能力更强。具体而言，图7(b)和图10(b)表明，MPC方案的控制效果比TRC和FTC方案更加平滑，这证明了MPC方案具有基于预测的全局调节能力而非局部调节能力。在两种不同的交通场景下，平均延误时间曲线的上升趋势较为明显，这是因为在整个仿真过程中交通流持续不断地被加载到道路网络中，导致交通延误不断累积。

此外，如图8(c)和(d)以及图11(c)和(d)所示，与基于第二节中所提出的预测模型的MPC方案相比，基于跟车预测模型的MPC方案在缓解交通拥堵方面的控制性能相对较差。这是因为所开发的非解析预测模型能够在滚动优化过程中结合有利的信号控制方案，精细地预测超出跟车行为的驾驶行为多样性。

图6(a)、7(a)、9(a)和10(a)中红色曲线的变化趋势几乎与绿色曲线重合，这表明基于Spark云的MPC方案的控制性能与单机环境下的MPC方案几乎相同。

D. 计算效率评估

基于Spark云的交通网络流量预测控制并行计算不仅实现了令人满意的控制性能，还提高了计算效率。在Spark云计算平台上配置了不同数量的节点，分别为4、10和64个。

图12描述了在控制周期（第三个控制周期）中不同进化代数的计算时间。如图12(a)所示，在单机环境中每一代的平均计算时间为119.9秒，而在使用4、10和64个节点的Spark云上分别为53.6秒、19.0秒和3.9秒。也就是说，在处理一代进化时，基于Spark的并行计算相较于单机环境分别快了66.3秒、100.9秒和116秒。相应地，与单机相比，加速比几乎分别集中在2.2、6.3和30.7，如图12(b)所示。此外，由于节点间的通信时间和计算负载影响，随着集群节点规模的增加，加速比呈非线性增长，如图12(c)所示。

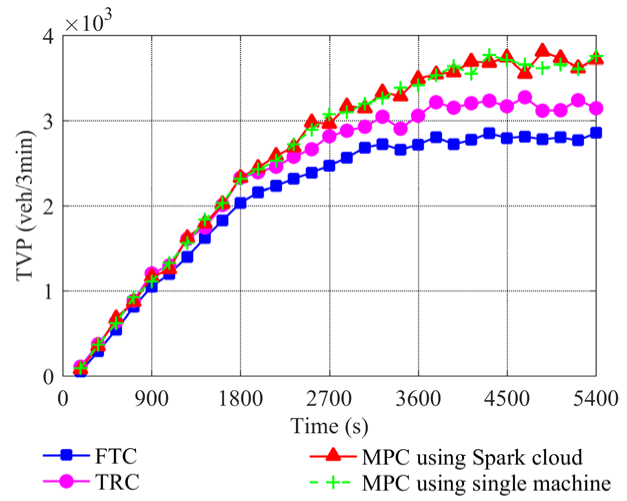
图13进一步显示了在单机和不同节点规模的Spark云计算条件下，所有控制周期的在线优化计算时间。如图13(a)所示，显然计算使用Spark云的MPC方案在每个控制时间步长上的计算速度远快于单机环境。具体而言，在单机计算环境中，所有染色体需要以循环方式逐一进行评估，因此计算负担相当大。相反，在基于Spark云的多节点计算环境中，当Spark集群上使用更多的执行器时，分配给每个执行器的染色体数量减少，从而相应地缩短了计算时间。在优化过程的早期阶段，如图13(b)所示，由于初始计算需要加载数据，随后将数据缓存到内存中以加速后续计算过程，因此图中的加速比较低。需要指出的是，具有64个节点的Spark计算集群可以在指定的控制周期180秒内完成计算任务（图13(a)中的红线），并满足交通网络流模型预测控制在线优化的实时性要求。

五、结论

我们提出了一种面向物联网/车联网背景下交通大数据处理与迭代计算任务的基于Spark云计算的交通网络流预测控制方法。该方法采用一种考虑跟车、全力加速和紧急制动等典型驾驶行为的非解析微观车辆运动模型作为预测模型，根据交通流反馈信息周期性地表征交通网络流的动态特性和分布。基于该非解析预测模型，我们借助RDD计算模型设计了两级分层并行遗传算法，以降低在线优化的计算时间负担。原始的顺序计算任务被分解为多个子任务，在相应的计算节点上以并行方式同时计算。所有中间结果均缓存在内存中，供Spark云在下一步迭代中进一步加快数据获取速度，相较于传统的云计算架构更具先进性。非解析模型预测控制器在Spark云计算平台上结合物联网/车联网通信技术，用于处理大数据驱动的决策任务。数值仿真结果验证了所提出的控制方案及并行实现方法在交通网络流量控制中的可行性。本文提供了一种基于Spark云的交通网络流预测控制解决方案，以满足在线非解析预测与优化的实时性要求。在未来研究中，我们将进一步改进预测模型和并行优化方法，以适用于大规模交通网络流预测控制。