递归牛顿-欧拉方法(Recursive Newton-Euler Method)是一种高效的动力学计算方法,尤其适用于串联多刚体系统,例如串联机械臂。递归牛顿-欧拉方法有正和逆两种形式,本文我们先来看正动力学。正动力学又称为前向动力学,如果给你机器人各关节的力矩后,通过正动力学可以求出机器人的运动。在这里,机器人的运动指各个关节(或者各连杆)的位置、速度和加速度。
下面的算法来自于论文《Lie Group Formulation of Articulated Rigid Body Dynamics》,我们更正了原文中的一处小错误。该算法使用了李群和李代数表示机器人连杆的坐标、速度和受力,其优点是形式简洁、线速度和角速度可以合写在一块,力也是如此,并有清晰的数学含义。该算法适用于三维空间,每一步正动力学计算过程包含三个递归子过程:1. 前向计算连杆的位姿和速度;2. 反向计算连杆系的广义惯量和偏置力;3. 前向计算加速度。在定义连杆的记号时,通常将固定的基座记为 0,与基座相连的连杆记为1,与连杆1相连的下一个连杆记为2,依次类推。这里把从基座开始向机械臂末端的方向称为前向(i 到 i+1),把机械臂末端到基座的方向称为反向(i 到 i-1)。
具体实现(Mathematica代码)
(*Initialization 部分参数初始化*)
time = 2000; dt = 0.005;
Table[mass[i] = 1; Gravity[i] = grav*mass[i]*{0, 0, -1, 0, 0, 0}, {i, 0, n, 1}];
Table[g[i, i + 1, 0] = RPToH[Id[3], {0, 0, (La[i] + La[i + 1])/2}], {i, 0, n - 1, 1}];
q = dq = ddq = ConstantArray[0, n];
Table[V[i] = dV[i] = ConstantArray[0, 6], {i, 0, n, 1}];
Table[M[i] = Id[6]; \[Tau][i] = 0, {i, n}];
F[n + 1] = ConstantArray[0, 6];
g[n, n + 1] = g[0, 0] = Id[4];
q = ConstantArray[Pi/2, n];
\[CapitalPi][n + 1] = Id[6]*0.0;
\[Beta][n + 1] = ConstantArray[0, 6];
Table[
qList = {qList, q};
gList = {gList, g[0, 4]};
(*Forward 前向递归*)
dq = dq + ddq*dt; (*欧拉积分*)
q = q + dq*dt;
For[i = 1, i <= n, i++,
g[i - 1, i] = TwistExp[\[Xi]r[i], q[[i]]].g[i - 1, i, 0];
g[0, i] = g[0, i - 1].g[i - 1, i];
V[i] = Ad[Iv[g[i - 1, i]]].V[i - 1] + \[Xi]s[i]*dq[[i]];
\[Eta][i] = ad[V[i] - \[Xi]s[i]*dq[[i]]].\[Xi]s[i]*dq[[i]];
];
(*Backward 反向递归*)
For[i = n, i >= 1, i--,
\[Tau][i] = 0;
Mh[i] = M[i] + T[Ad[Iv[g[i, i + 1]]]].\[CapitalPi][i + 1].Ad[Iv[g[i, i + 1]]];
Fext[i] = T[Ad[RPToH[R[g[0, i]], {0, 0, 0}]]].Gravity[i];
\[ScriptCapitalB][i] = -T[ad[V[i]]].M[i].V[i] - Fext[i] + T[Ad[Iv[g[i, i + 1]]]].\[Beta][i + 1];
\[CapitalPsi][i] = 1/(\[Xi]s[i].Mh[i].\[Xi]s[i]);
\[CapitalPi][i] = Mh[i] - \[CapitalPsi][i]*KroneckerProduct[Mh[i].\[Xi]s[i], \[Xi]s[i].Mh[i]];
\[Beta][i] = \[ScriptCapitalB][i] + Mh[i].(\[Eta][i] + \[Xi]s[i]*\[CapitalPsi][i]*(\[Tau][i] - \[Xi]s[i].(Mh[i].\[Eta][i] + \[ScriptCapitalB][i])));
];
(*Forward 前向递归*)
For[i = 1, i <= n, i++,
ddq[[i]] = \[CapitalPsi][i]*(\[Tau][i] - \[Xi]s[i].Mh[i].(Ad[Iv[g[i - 1, i]]].dV[i - 1] + \[Eta][i]) - \[Xi]s[i].\[ScriptCapitalB][i]);
dV[i] = Ad[Iv[g[i - 1, i]]].dV[i - 1] + \[Xi]s[i]*ddq[[i]] + \[Eta][i]];
, {t, time}]; 仿真结果
我们首先以简单的 4 个连杆组成的机械臂为例进行仿真试验,连杆之间用转动关节连接,机器人初始时刻处于水平的静止状态,所有关节的力矩设为0。理论上机器人应该在重力作用下自由下落,我们看看用正向动力学步骤计算得到的仿真结果是什么样的。结果如下动画所示(只显示了Y-Z平面)。从结果看好像是对的,但是我还不敢100%保证。
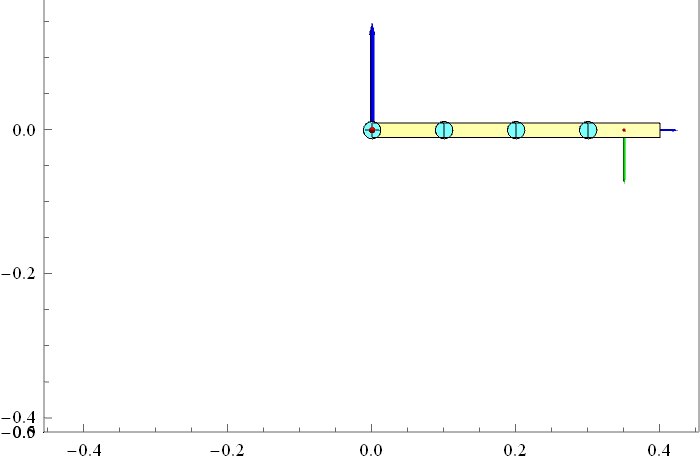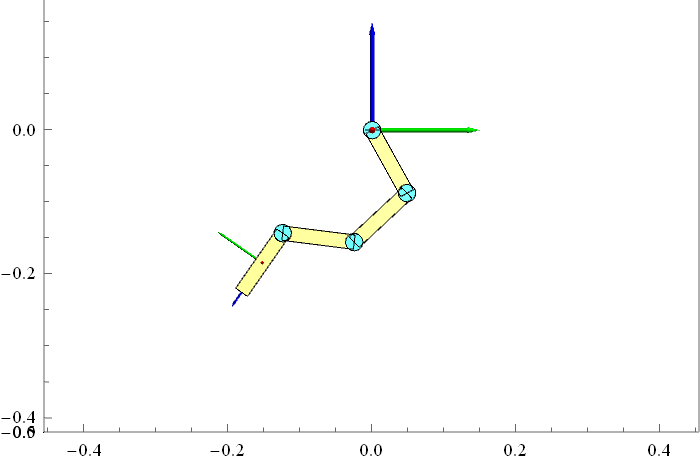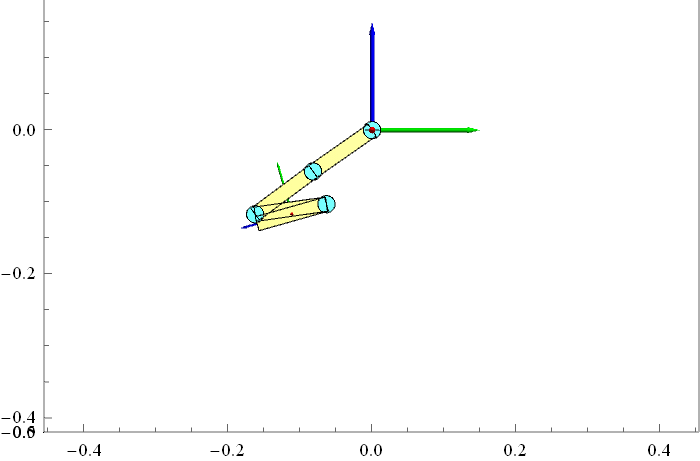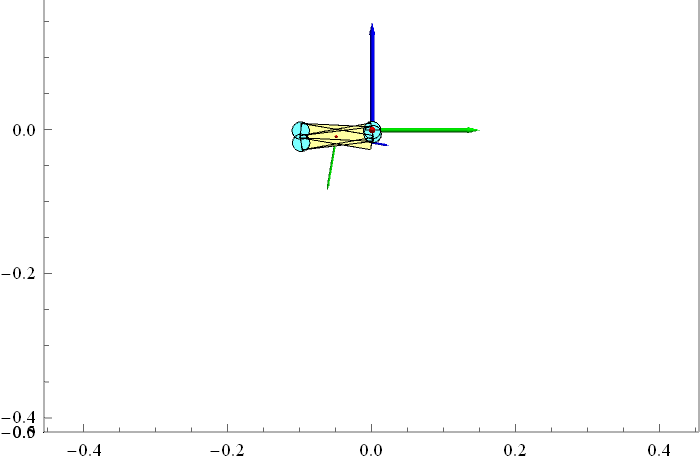
正确性验证
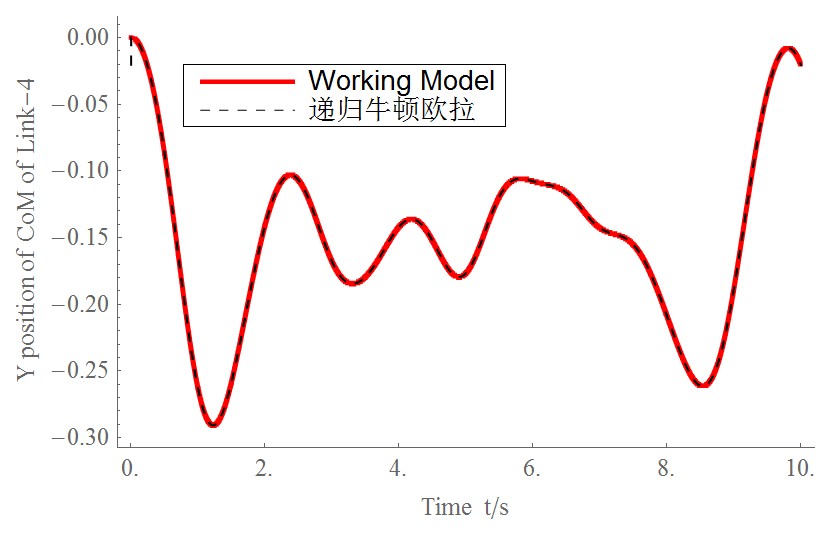
为了验证算法的正确性,我和第三方的仿真软件进行对比。这里我选取了Working Model软件(是一款商业的二维动力学仿真软件)。在Working Model中设置相同的参数和初始状态,仿真过程如下图所示。
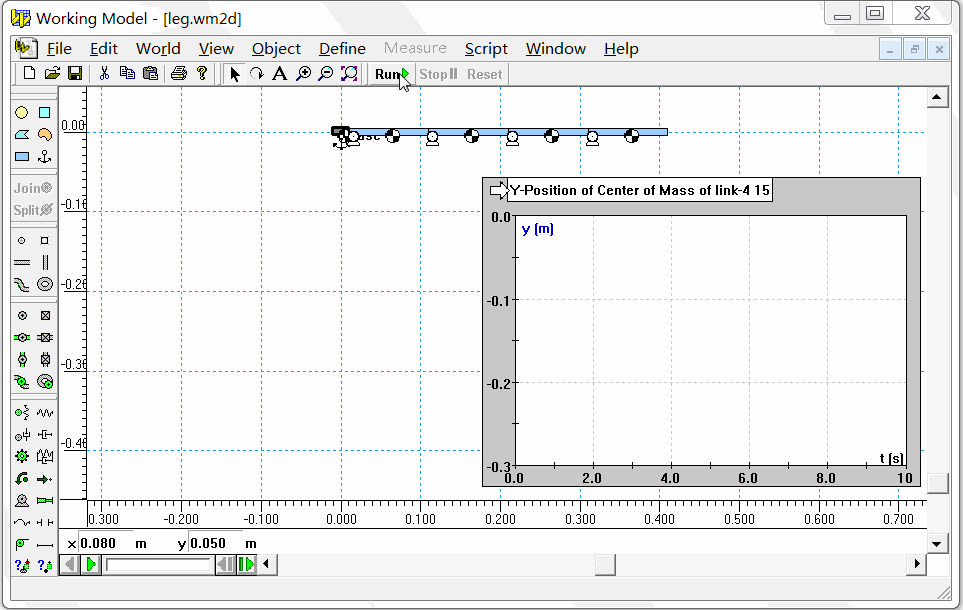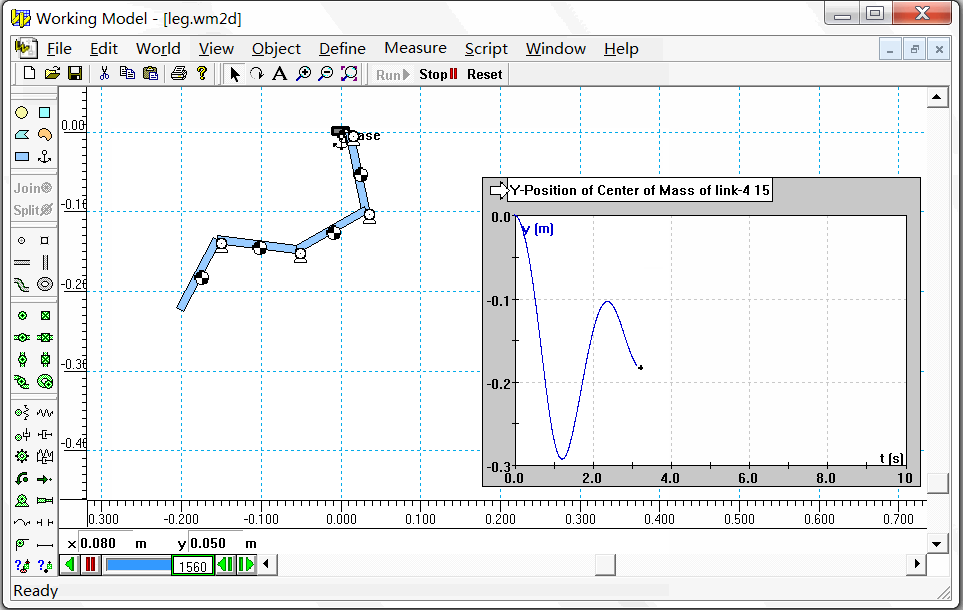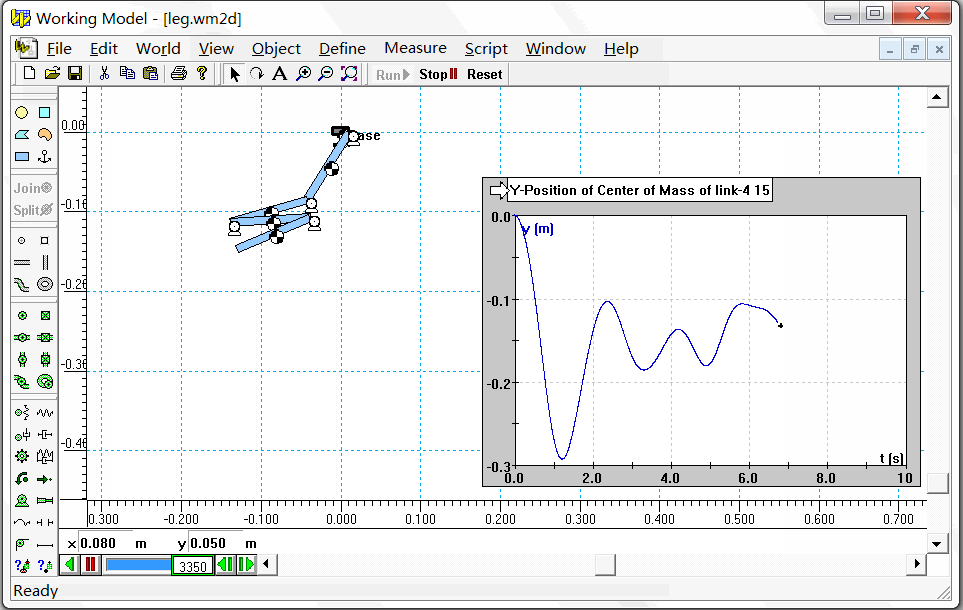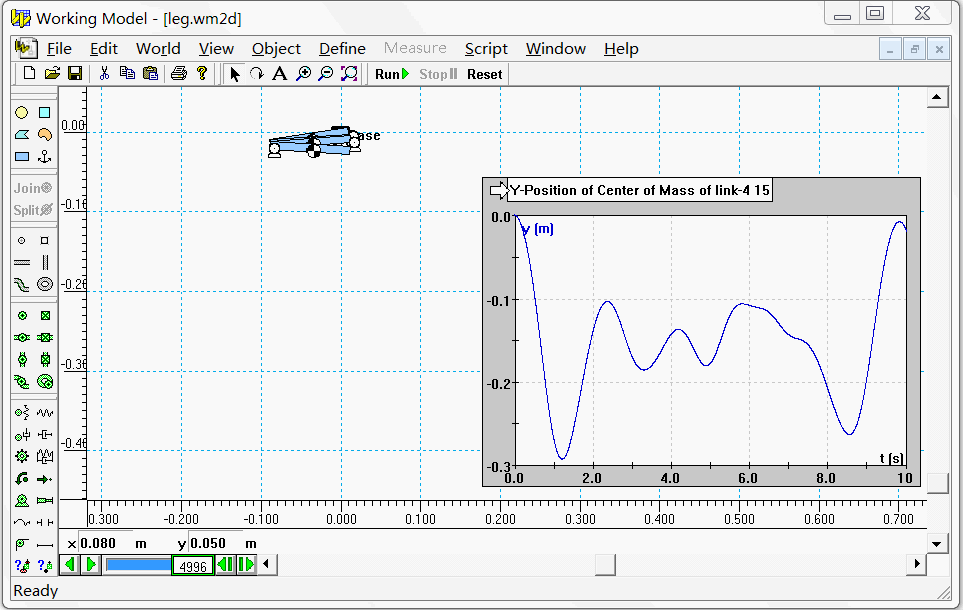
我们选择末端连杆(也就是第4个连杆)质心的Y坐标(重力加速度的反方向)进行对比,结果如下图左所示。二者的误差(下图右)在-0.001m~0.001m之间。考虑到每个连杆的长度为10cm,误差<1mm 说明我们算法基本是正确的。因为都是数值计算,有误差应该是正常的。至于为什么误差在0.5mm这个量级,这可能和我们采用的积分方法有关。在上面的算法中,我们采用了最简单的欧拉积分。而在Working Model中,因为这个软件不是开源的,我们也看不到它的积分方法是怎样实现的。不过我们倒是可以设置,在Edit菜单下的Accuracy选项中即可选择积分方法并设置积分步长。

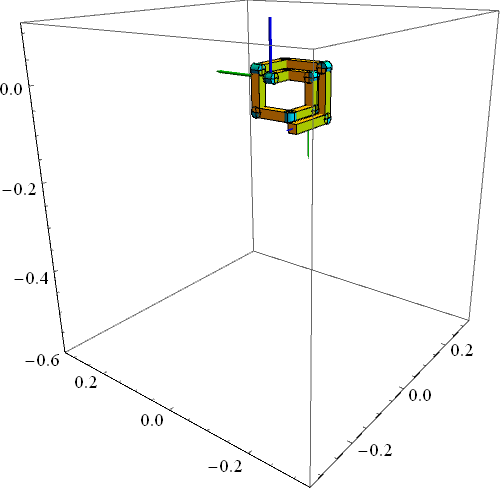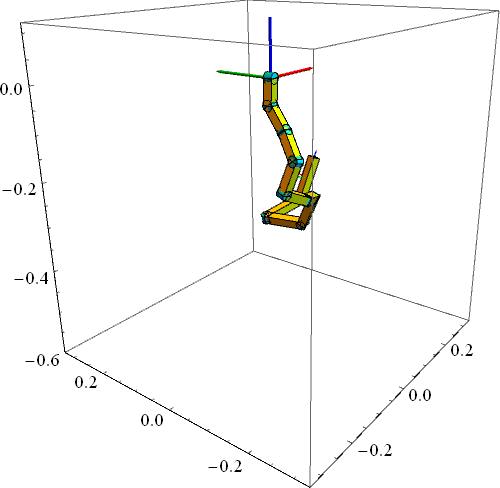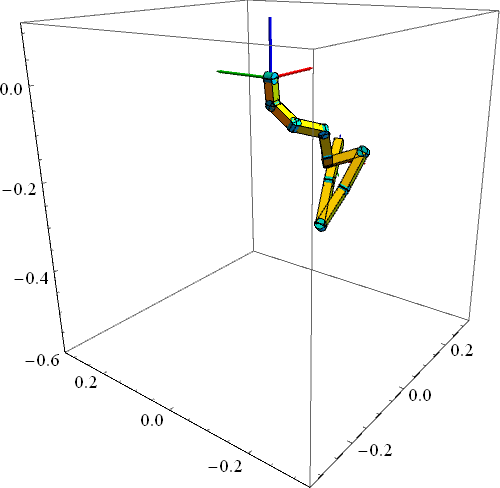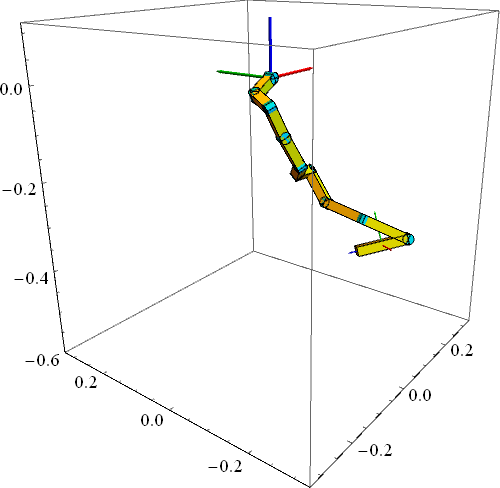
下图中的例子是10自由度的连杆同样只在重力作用下(关节力矩为0)的运动,只是初始状态不同,而且每相邻的两个关节旋转轴相互垂直。有没有闻到一丝混沌(Chaos)的味道
上面我们介绍了正动力学的计算过程,也就是给定力矩后计算机械臂的运动。本文介绍逆动力学,也就是在机器人的运动已知的情况下反求所需的关节力矩。算法同样来自于论文《Lie Group Formulation of Articulated Rigid Body Dynamics》(下图中画红线的是错误的地方)。这篇论文使用了李群等高等数学知识,如果你感到陌生可以阅读《A Mathematical Introduction to Robotic Manipulation》,该书恰好缺少递归牛顿欧拉动力学的介绍。如果有了前面的数学基础知识,读懂下面的公式其实并不难。

每步逆动力学计算过程包含两个递归子过程:1. 前向计算速度和加速度;2. 反向计算力矩。这要比正动力学相对简单一些。你是不是好奇:为什么逆动力学包含这两步,为什么不是反过来:反向计算速度及加速度和前向计算力矩?其实仔细一思考你就能理解,原因很简单(需要一点点理论力学的知识):逆动力学的输入是机械臂的运动(包括关节的速度和加速度)。由于基座的速度和加速度是已知的(永远是零),而后一个连杆的速度显然依赖前一个连杆的速度,这是因为机械臂的关节角度是相对于上一个连杆定义的,所以,从基座出发一直向前,直到机械臂末端的连杆,所有连杆质心的速度和加速度都可以算出来。至于力矩嘛,如果我们选择中间任何一个连杆,它两侧的受力(也就是和它相连的连杆对它的反作用力)都是未知的。唯独末端的连杆,它一侧的受力是已知的(为零或者给定)。前向过程已经计算出来了加速度,我们可以借助单刚体的牛顿-欧拉方程求出它另一侧的受力。因为每两个相邻的连杆受到大小相等,方向相反的相互作用力,我们就知道了它前一个连杆一侧的受力。依次向基座的方向(反向)计算,我们可以求出后面所有连杆的受力。所以,力矩的递归是反向的。
具体实现(Mathematica代码)
time = 2000; dt = 0.001;
Table[mass[i] = 1; Gravity[i] = grav*mass[i]*{0, 0, -1, 0, 0, 0}, {i, 0, n, 1}];
Table[g[i, i + 1, 0] = RPToH[Id[3], {0, 0, (La[i] + La[i + 1])/2}], {i, 0, n - 1, 1}];
q = dq = ddq = ConstantArray[0, n];
q[[1]] = -3 Pi/4;
Table[V[i] = dV[i] = ConstantArray[0, 6], {i, 0, n, 1}];
Table[M[i] = Id[6]; \[Tau][i] = 0, {i, n}];
F[n + 1] = ConstantArray[0, 6];
g[n, n + 1] = g[0, 0] = Id[4];
qList = gList = \[Tau]List = {};
dq = ConstantArray[-0.6, n];
Table[
qList = {qList, q};
gList = {gList, g[0, n]};
\[Tau]List = {\[Tau]List, Array[\[Tau], n]};
q = q + dq*dt;
(*Forward*)
For[i = 1, i <= n, i++,
g[i - 1, i] = TwistExp[\[Xi]r[i], q[[i]]].g[i - 1, i, 0];
g[0, i] = g[0, i - 1].g[i - 1, i];
V[i] = Ad[Iv[g[i - 1, i]]].V[i - 1] + \[Xi]s[i]*dq[[i]];
dV[i] = Ad[Iv[g[i - 1, i]]].dV[i - 1] + ad[V[i] - \[Xi]s[i]*dq[[i]]].\[Xi]s[i]*dq[[i]] + \[Xi]s[i]*ddq[[i]];
];
(*Backward*)
For[i = n, i >= 1, i--,
Fext[i] = T[Ad[RPToH[R[g[0, i]], {0, 0, 0}]]].Gravity[i];
F[i] = M[i].dV[i] - T[ad[V[i]]].M[i].V[i] + T[Ad[Iv[g[i, i + 1]]]].F[i + 1] - Fext[i];
\[Tau][i] = \[Xi]s[i].F[i];
];
, {t, time}];仿真结果
我们选择6个连杆进行仿真试验,连杆之间用转动关节连接,所有关节的速度都设为常数-0.6 rad/s。给定关节速度下,机器人的运动如下图左所示(显示了Y-Z平面)。逆动力学求得的关节力矩如下图右所示。
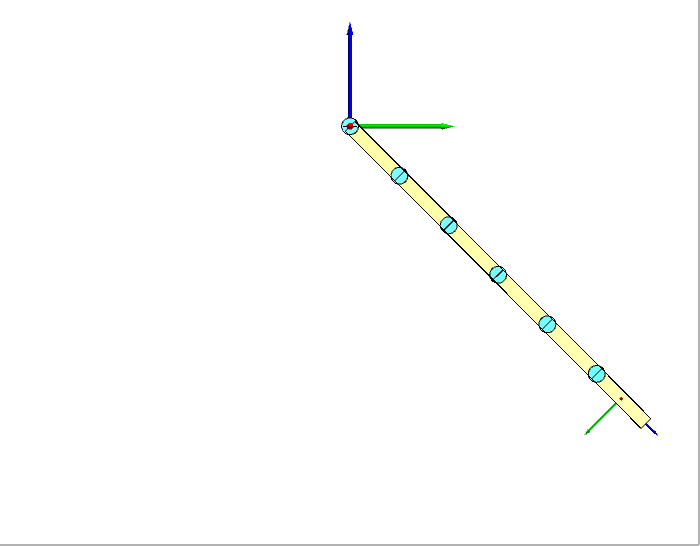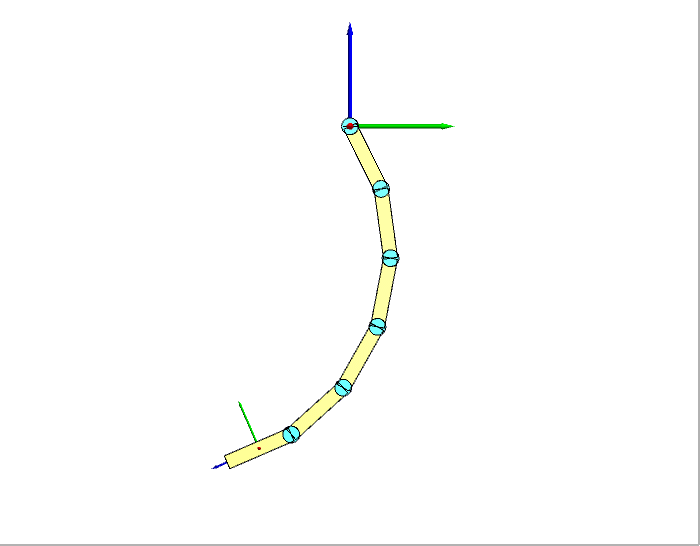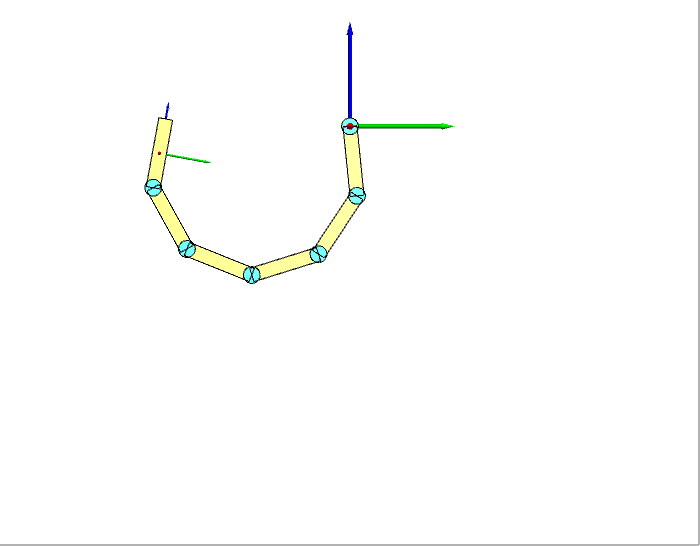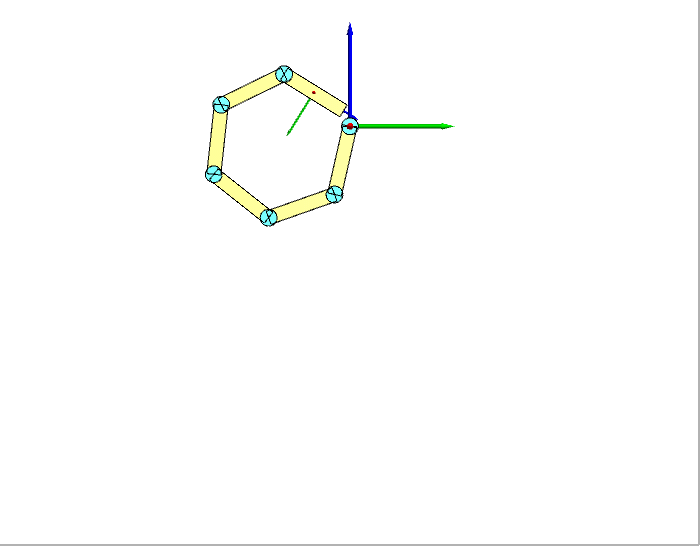
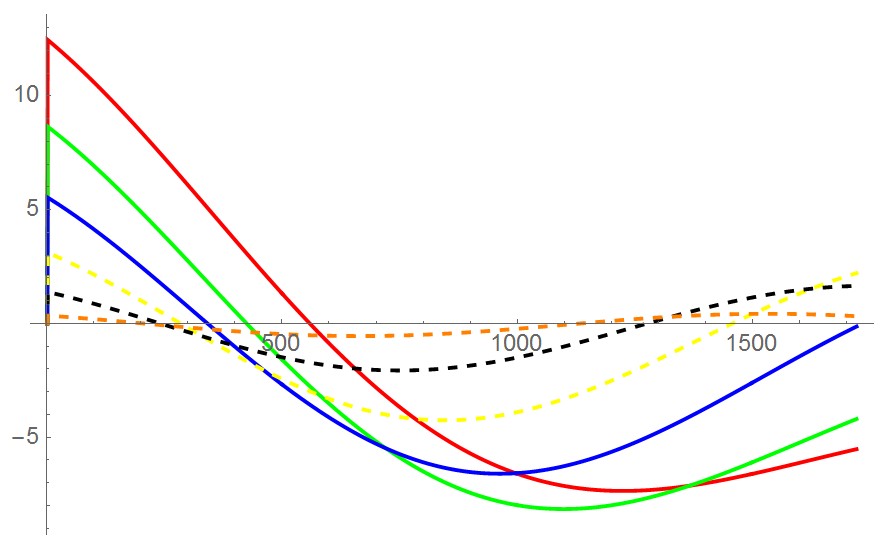
正确性验证
为了验证逆动力学算法的正确性,我们借助前面得到的正动力学:将逆动力学求得的力矩带入正动力学进行仿真,看看机器人的运动与我们设定的运动是否相同,整个过程就是一个闭环,如下图:
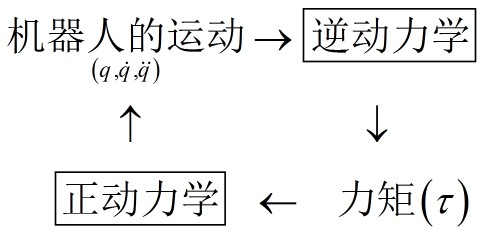
正动力学仿真的结果如下图所示。可以看到结果与我们给定的运动一模一样,这证明我们的逆动力学是正确的。
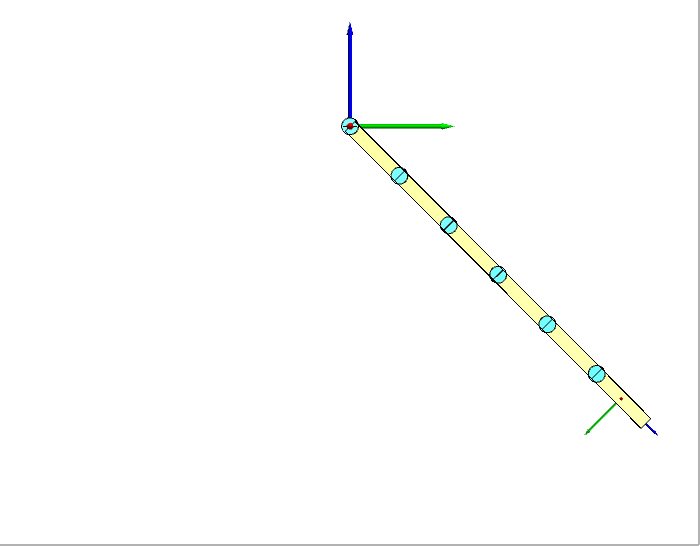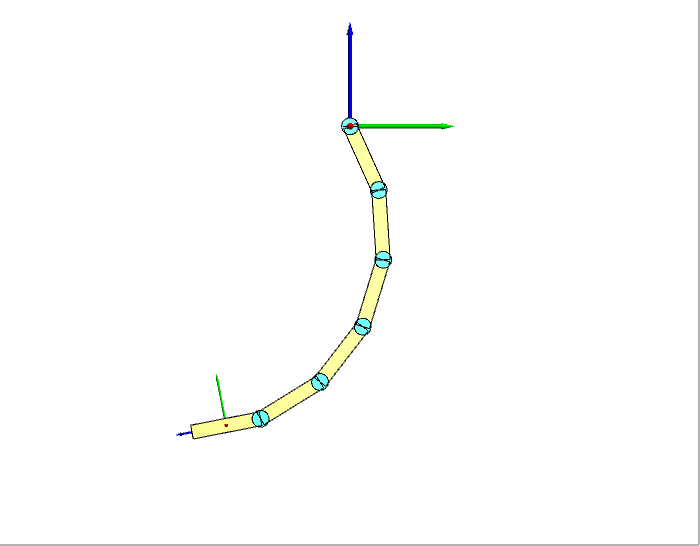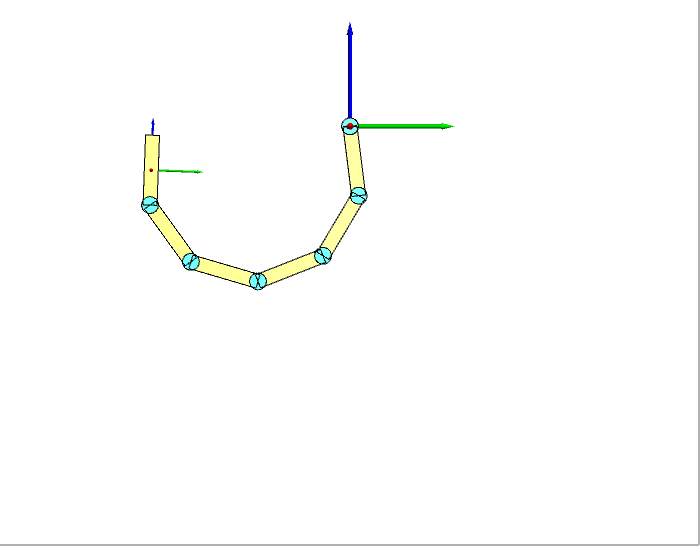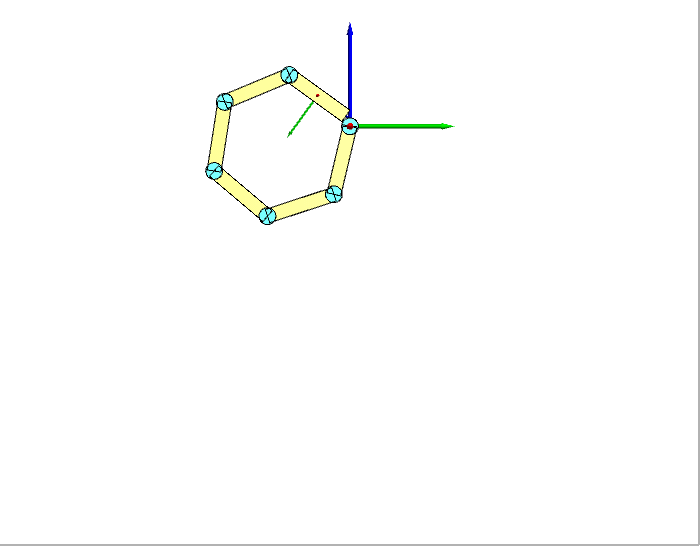







 本文介绍递归牛顿-欧拉方法在串联多刚体系统动力学计算中的应用,涵盖正动力学与逆动力学的原理及Mathematica实现,并通过仿真验证算法的准确性。
本文介绍递归牛顿-欧拉方法在串联多刚体系统动力学计算中的应用,涵盖正动力学与逆动力学的原理及Mathematica实现,并通过仿真验证算法的准确性。
















 6990
6990

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








