信号与频谱（一）

**

写在前面

前面大概将通信系统整体模型和流程有所了解，肯定会有很多疑问，下面将会分部分从底层阐述建立知识体系。

**
1 概述
一种方法是在时域观察信号波形的变化，另一种方法是在频域观察信号频谱的变化。
任何复杂的信号都可以分解成一系列不同频率的基本信号之和，一般用频谱来反映构成信号的所有频率成分。
基本信号我们很容易想到正弦信号
2 正弦信号
积分特性

正交特性


3 复指数信号
欧拉公式之后，复指数信号作为基本信号进行频谱分析时使用复指数运算，比较简洁，很快取代了正弦信号的基本信号地位。
（一）那么如何理解复数呢
复数与复指数ejθ相乘就可以用向量旋转来理解。
复数与复指数ejθ相乘，相当于复数对应的向量旋转角度θ：
θ>0逆时针旋转
θ<0顺时针旋转
（二）那么如何理解虚数呢？
数学中的虚数一般用“i”表示，为何物理中一般用“j”表示呢？这是因为物理中经常用“i”表示电流。
感觉高中课本纯粹就是为了给x^2=-1一个解，才定义了虚数i，其平方为-1，至于虚数i有什么物理意义就不得而知了
复数与j相乘，就是与复指数exp(jpi/2)相乘，相当于复数对应的向量逆时针旋转90°。

用图很容易理解虚数的物理意义
（三）如何理解复信号呢？
1．复指数信号的几何意义
复平面上的一个长度为A的旋转向量，始端位于原点，从角度φ开始，以角速度ω0围绕原点旋转，其末端在复平面上的轨迹就是复指数信号s(t)=Ae^j(w0t+phase)。
由复指数信号在复平面上的投影是个圆，很容易让人想起物理中学过的李萨育图形。

至此你是否对复信号有了一定的猜测
没错！
2.复信号的本质就是并行传输的2路实信号。
为什么要这样表示呢？
fft中这样可以加快运算速度，对一个复信号进行fft可以得出两个实信号的fft
引入复信号只是为了便于描述和处理信号而已，实际通信系统中都是并行传输2路实信号，并没有传输虚数j。
（四）复指数信号的特性
积分特性
当积分区间取复指数信号周期的整数倍时，积分结果为零。
正交特性
任意1个复指数信号与另1个复指数信号共轭的乘积在基波周期内的积分结果都为0。
任意1个复指数信号与自身共轭的乘积在基波周期内的积分结果都为T0。
4.信号的相和相位
第一种：相，有规律的循环变化周期中的一个特定现象或状态。
a particular appearance or state in a regularly recurring cycle of changes.
第二种：相位，从指定参考点开始测量的完整周期已经过去的部分，通常用角表示，所以又被称为相角。
The fraction of a complete cycle elapsed as measured from a specified reference point and often expressed as an angle.
零相位：起始点离t=0时刻最近的那个完整周期的起始点相位为零。
完整周期：注意正弦余弦不同，f>0,f<0也不同
正相位：f>0 延时间轴正向相位逐渐增大，零相位右侧为正相位
初始相位：t=0时刻的相位（<=180度）
利用旋转向量理解相位：

正弦波的初相和相位（f>0 初相大于0）

正弦波的初相和相位（f>0 初相小于0）
相位差：
当我们说相位差的时候，已经隐含了两个信号频率相同的意思。
两个同频信号的相位差就等于初相之差
超前和滞后：
超前和滞后向量图（相位差绝对值小于π）
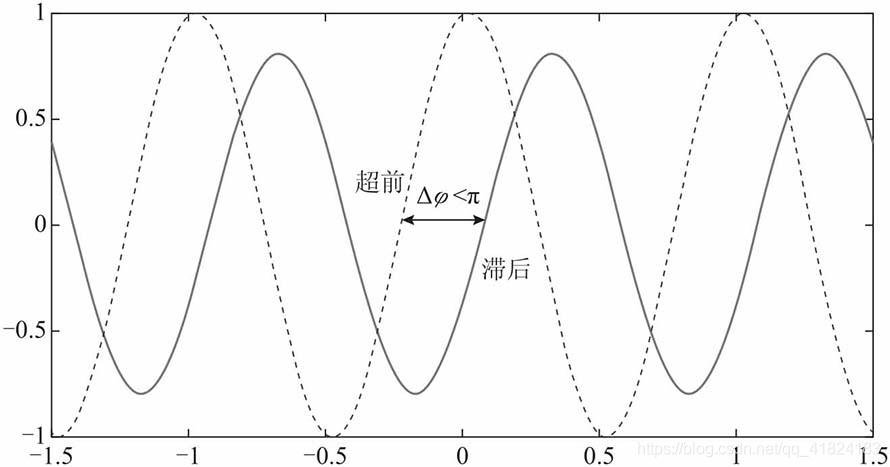超前和滞后波形图（相位差绝对值小于π）
波的干涉：

波的相干条件：频率相同，相位差恒定，振动方向相同。
相长干涉：接收到的两个波源信号正好同相，合成信号幅度等于二者幅度之和，这种情况被称为相长干涉
相消干涉：接收到的两个波源信号正好反相，合成信号幅度等于二者幅度之差，这种情况被称为相消干涉。
5.信号的分解和合成
（一）正弦信号作为基本信号
以周期方波来为例

周期为1s
分解：

幅度0.5的直流信号
0.637幅度 1Hz的余弦信号
合成如下：


0.212 3Hz

再叠加0.127 5Hz

可以想象，随着叠加的余弦信号越来越多，合成信号的波形越来越逼近一个方波，这从一个侧面说明了：可以将方波信号分解成一个直流分量和一系列余弦波分量之和。
（二）复指数信号作为基本信号

幅度0.5 直流

幅度0.318 1Hz复指数信号

幅度0.318 -1Hz
叠加如下：

0.106 3

0.106 -3
叠加如下：

再叠加0.063 5和-5Hz的复指数信号如下：
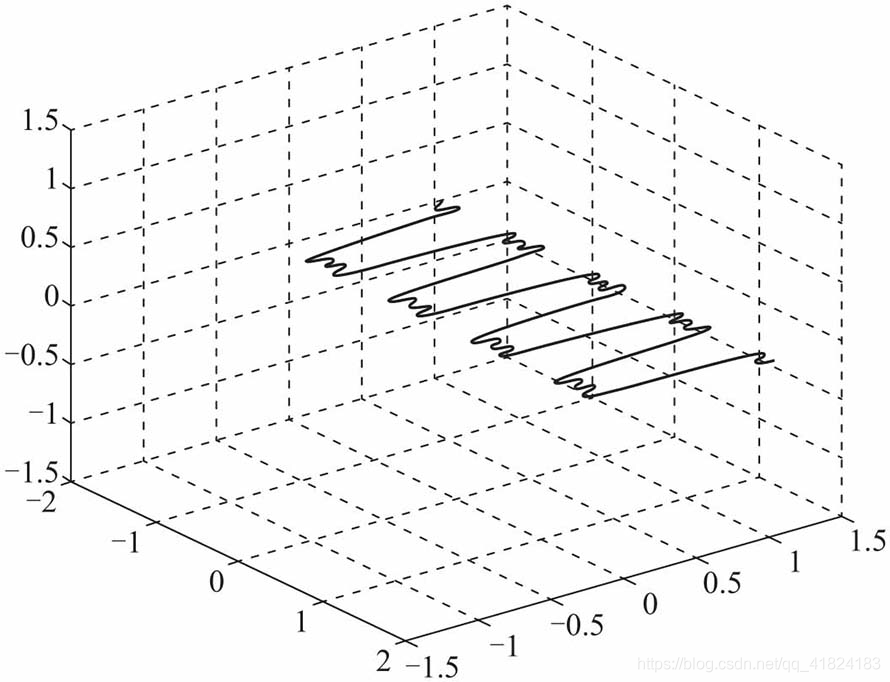可以想象，随着叠加的复指数信号越来越多，波形越来越逼近一个方波，这从一个侧面说明：可以将方波信号分解成一个直流分量和一系列复指数信号分量之和。
**

写在后面

这一部分分成两篇写，下一遍将是有关信号与系统方面的傅里叶级数和傅里叶变换，以及离散傅里叶变换，它们的区别和需要注意的地方。
**