循环神经网络：时间序列数据的处理

原创已于 2025-09-03 17:14:06 修改 · 866 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#循环神经网络 #长短时记忆网络 #门控循环单元

于 2025-09-03 08:30:00 首次发布

神经网络的数学之美专栏收录该内容

12 篇文章

订阅专栏

在数据驱动时代，时间序列数据无处不在，从股票市场的波动到天气变化的记录，再到各种传感器采集的信号，这些数据都蕴含着丰富的信息。

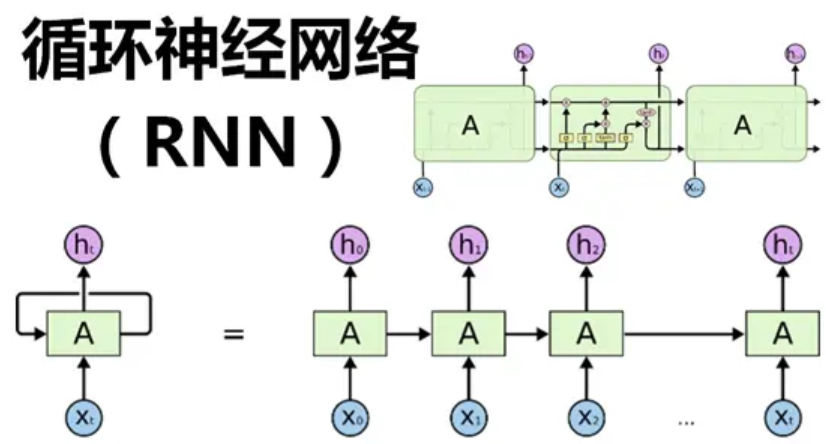
循环神经网络（Recurrent Neural Network，简称RNN）作为一种强大的工具，能够有效处理这类具有时间依赖性的数据。

今天，就让我们深入探讨循环神经网络的数学原理，揭开它处理时间序列数据的神秘面纱。

一、RNN的基本结构与原理

循环神经网络（RNN）是一种专门用于处理序列数据的神经网络架构。

与传统的前馈神经网络不同，RNN在结构上引入了循环连接，使得网络能够记忆之前的信息，并将其用于当前的计算。

图1. RNN与FNN的结构示意图

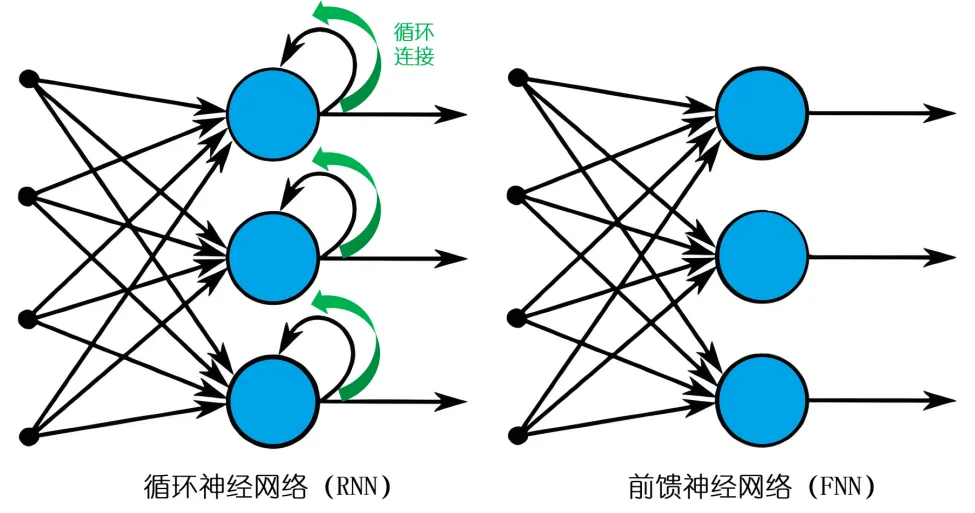
这种特性使得RNN非常适合处理时间序列数据，因为时间序列数据中的每个数据点都与之前的点存在关联。

从结构上看，RNN由多个神经元组成，这些神经元在时间序列的每个时间步上都会接收输入数据，并输出一个结果。

同时，神经元会将当前的输出作为下一个时间步的输入，从而形成一个循环。这种循环结构使得RNN能够捕捉到时间序列中的动态变化。

图2. RNN循环单元结构

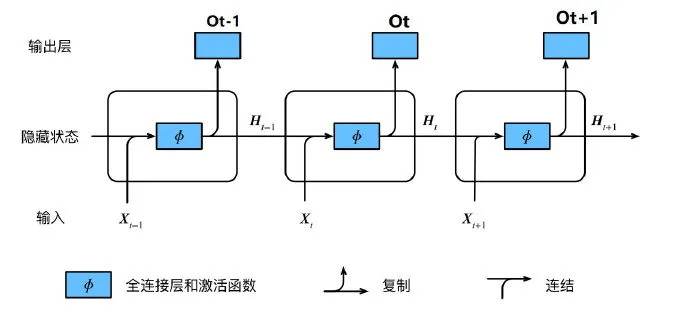
RNN的基本思想是将时间序列数据分解为一个个时间步，然后在每个时间步上进行信息的传递和更新。

假设我们有一个时间序列 ${x1,x2,…,xT}\{x_1, x_2, \ldots, x_T\}$ ，其中 $T$ 是时间序列的长度。在每个时间步 $t$ ，RNN会接收当前的输入 $x_t$ 和上一个时间步的隐藏状态 $h_{t-1}$ ，然后通过一个状态转移方程计算出当前的隐藏状态 $h_t$ 。

二、 RNN中的时间步与状态更新

在RNN中，时间步是处理时间序列数据的基本单位。每个时间步对应序列中的一个数据点，网络会依次处理这些数据点，并在每个时间步更新其内部状态。

图3. RNN中的时间步与状态更新

RNN的状态更新过程可以用一个简单的数学公式来描述。

假设在时间步 $t$ 时，输入为 $x_t$ ，隐藏层的状态为 $h_t$ ，那么状态更新公式可以表示为：
$h_t = f(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$
其中， $f$ 是一个非线性激活函数，如 $T anh$ 或 $R e LU$ ； $W_{hh}$ 和 $W_{xh}$ 是权重矩阵，分别表示隐藏层到隐藏层的连接权重和输入层到隐藏层的连接权重； $b_h$ 是偏置项。

这个公式的核心在于，当前时刻的隐藏状态 $h_t$ 不仅取决于当前输入 $x_t$ ，还取决于上一时刻的隐藏状态 $h_{t-1}$ 。这种依赖关系使得RNN能够捕捉到时间序列中的动态变化。

这种状态更新机制使得RNN能够将历史信息传递到当前时间步，从而捕捉到序列中的时间依赖性。

三、RNN的数学推导

循环神经网络的状态转移方程是其数学原理的核心。状态转移方程描述了隐藏状态如何从一个时间步转移到下一个时间步。

图4. RNN循环单元

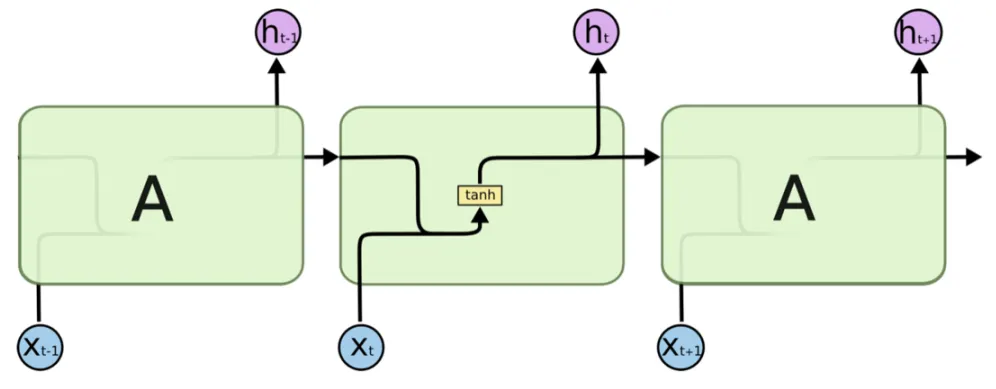
以简单循环神经网络（Simple RNN）为例，其状态转移方程可以表示为：
$h_t = f(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$

然而，简单 RNN 在处理长序列数据时存在梯度消失和梯度爆炸的问题，这使得网络难以捕捉到长距离的时间依赖关系。

为了解决这一问题，人们提出了长短期记忆网络（LSTM）和门控循环单元（GRU）。

3.1 LSTM的数学原理

LSTM是一种能够有效解决梯度消失问题的循环神经网络架构。它的核心思想是引入了“门”的概念，通过控制信息的流动来保持长期依赖关系。

图5. LSTM门控单元

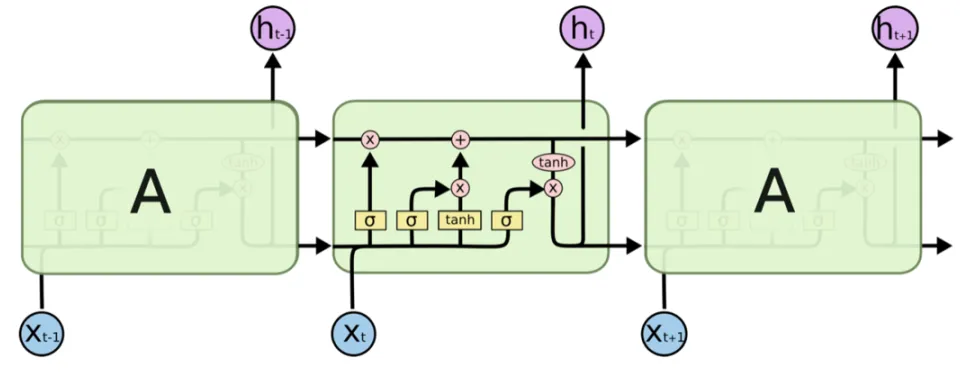
LSTM的结构比普通的RNN复杂得多，它包含三个主要的门：遗忘门、输入门和输出门。

1. 遗忘门（Forget Gate）

遗忘门的作用是决定从细胞状态中丢弃哪些信息。遗忘门会读取上一个时间步的隐藏状态 $h_{t-1}$ 和当前时间步的输入 $x_t$ ，然后通过一个sigmoid激活函数计算出一个介于0和1之间的值，表示要丢弃的信息的比例。

遗忘门的计算公式为：
$ft=σ(Wf[ht−1,xt]+bf)f_t = \sigma(W_f[h_{t-1}, x_t] + b_f)$
其中， $W_f$ 是遗忘门的权重矩阵， $b_f$ 是偏置项。

2. 输入门（Input Gate）

输入门的作用是决定哪些新的信息要写入到细胞状态中。输入门包含两部分：一部分是通过sigmoid激活函数计算出的输入门的值 $i_t$ ，表示要写入的信息的比例；另一部分是通过tanh激活函数计算出的候选值 $C~t\tilde{C}_t$ ，表示要写入的信息的内容。

输入门的计算公式为：
$it=σ(Wi[ht−1,xt]+bi)C~t=tanh⁡(Wc[ht−1,xt]+bc)i_t = \sigma(W_i[h_{t-1}, x_t] + b_i) \\ \tilde{C}_t = \tanh(W_c[h_{t-1}, x_t] + b_c)$
其中， $W_i$ 和 $W_c$ 分别是输入门和候选值的权重矩阵， $b_i$ 和 $b_c$ 是偏置项。

3. 细胞状态（Cell State）

细胞状态是LSTM的核心部分，它负责存储长期依赖信息。

细胞状态的更新公式为：
$Ct=ft⋅Ct−1+it⋅C~tC_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t$

这个公式表示细胞状态是由上一个时间步的细胞状态经过遗忘门的筛选后，再加上新的输入信息组成的。

4. 输出门（Output Gate）

输出门的作用是决定细胞状态中哪些信息要输出到隐藏状态中。

输出门的计算公式为：
$ot=σ(Wo[ht−1,xt]+bo)ht=ot⋅tanh⁡(Ct)o_t = \sigma(W_o[h_{t-1}, x_t] + b_o) \\ h_t = o_t \cdot \tanh(C_t)$
其中， $W_o$ 是输出门的权重矩阵， $b_o$ 是偏置项。

通过这种复杂的门控机制，LSTM能够有效地保持长期依赖关系，从而在处理长序列数据时表现出色。

3.2 GRU的数学形式

GRU是另一种改进的循环神经网络架构，它的结构比LSTM简单，但同样能够有效地解决梯度消失问题。

图6. GRU门控单元

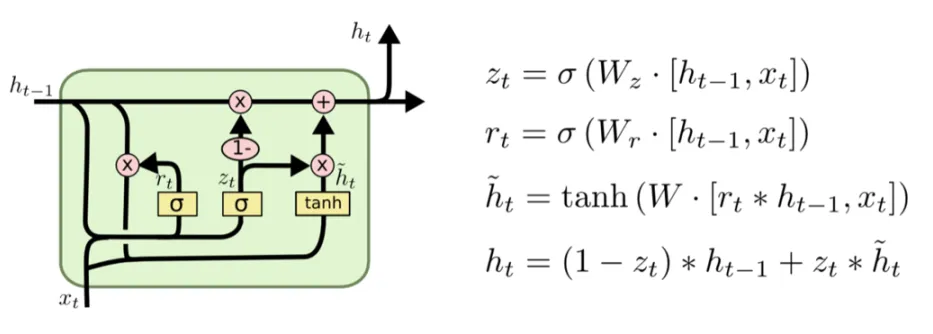
GRU的核心思想是将LSTM中的遗忘门和输入门合并为一个更新门，同时引入了一个重置门来控制信息的流动。

1. 更新门（Update Gate）

更新门的作用是决定从上一个时间步的隐藏状态中保留多少信息，以及从当前时间步的输入中获取多少信息。

更新门的计算公式为：
$zt=σ(Wz[ht−1,xt]+bz)z_t = \sigma(W_z[h_{t-1}, x_t] + b_z)$
其中， $W_z$ 是更新门的权重矩阵， $b_z$ 是偏置项。

2. 重置门（Reset Gate）

重置门的作用是决定上一个时间步的隐藏状态对当前时间步的影响程度。

重置门的计算公式为：
$rt=σ(Wr[ht−1,xt]+br)r_t = \sigma(W_r[h_{t-1}, x_t] + b_r)$
其中， $W_r$ 是重置门的权重矩阵， $b_r$ 是偏置项。

3. 隐藏状态的更新

隐藏状态更新公式表示隐藏状态是由上一个时间步的隐藏状态和当前时间步的候选隐藏状态加权组合而成的。

在GRU中，隐藏状态的更新公式为：
$h~t=tanh⁡(W[rt⋅ht−1,xt]+b)ht=(1−zt)⋅ht−1+zt⋅h~t\tilde{h}_t = \tanh(W[r_t \cdot h_{t-1}, x_t] + b) \\ h_t = (1 - z_t) \cdot h_{t-1} + z_t \cdot \tilde{h}_t$
其中， $W$ 是权重矩阵， $b$ 是偏置项。