正则化的艺术：从数学原理到过拟合的防御机制

在深度学习领域，神经网络如同一位充满潜力的艺术家，但如果不加以适当的引导，它很容易陷入“过拟合” 的泥沼。

过拟合，就像艺术家过于执着于画布上的每一个细节，却忽略了整个作品的和谐与美感。

今天，我们将深入了解正则化的数学原理，探究其如何助力神经网络在复杂数据环境中维持良好泛化性能。

一、过拟合的数学分析

过拟合，是神经网络训练过程中一个让人头疼的问题。

简单来说，过拟合就是模型在训练数据上表现得过于完美，但在新的测试数据上却表现糟糕。

图1. 不同任务的过拟合现象

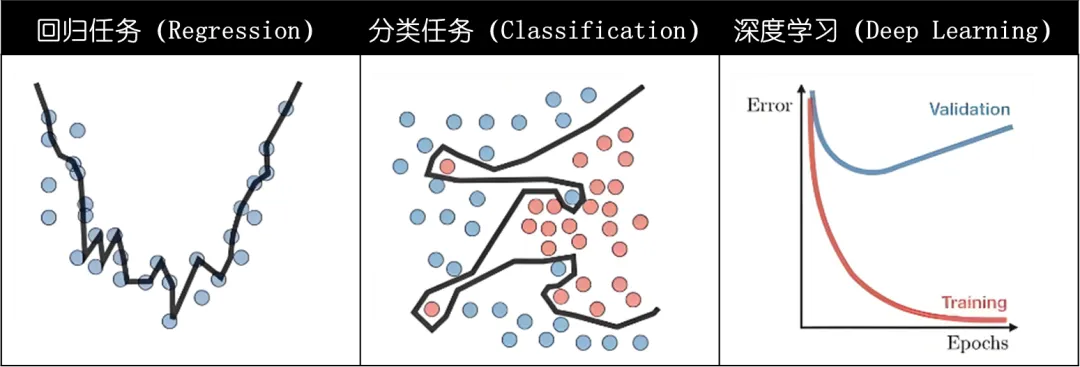
而从数学角度来看，这主要是因为模型过于复杂，参数过多，导致模型能够记住训练数据中的每一个细节，甚至是噪声。

---

但这种拟合的准确率是虚假的，它无法在的数据上应用。

比如，一个有很多隐藏层和大量神经元的网络，参数可能有几百万甚至更多。这种网络很容易去“迎合”训练数据里的噪声和异常值，让自己在训练集上准确率特别高。

而且在实际应用中，我们用于训练的数据往往是有限的。如果模型复杂度很高，有限的训练数据无法为模型提供足够的信息来学习数据的真实分布。

图2. 不同任务测试集与训练集的分布差异

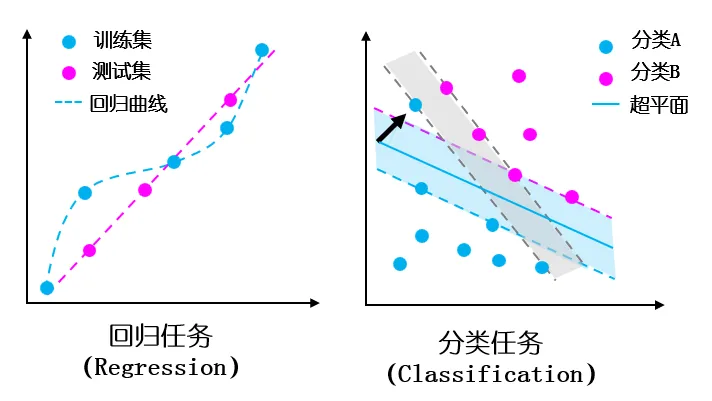
模型可能会过度依赖训练数据中的某些特定模式，而这些模式在测试数据中可能不存在。

二、正则化的数学原理

正则化是防止模型过拟合的常用技术，它主要是通过约束模型复杂度来提高模型的泛化能力。

常见的正则化方法包括 $L1$ 正则化、$L2$ 正则化和Dropout技术。

2.1 $L1$ 正则化：稀疏之美

$L1$ 正则化通过在损失函数中加入权重的绝对值之和（即 $L1$范数）作为惩罚项来限制模型的复杂度。

其数学形式为：
$$L_{L1}(\mathbf{w})=L(\mathbf{w})+\lambda \sum _i|w_i|$$
其中，$L(\mathbf{w})$ 是原始损失函数，$\lambda$ 是正则化参数，wiw_i