手把手带你推导“线性回归”核心公式

最新推荐文章于 2025-12-03 18:58:14 发布

原创最新推荐文章于 2025-12-03 18:58:14 发布 · 1.3k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#线性回归 #机器学习 #回归

手推机器学习公式专栏收录该内容

12 篇文章

订阅专栏

在机器学习中，线性回归是最基础、最经典的模型之一。它简单易懂，却又强大无比，被广泛应用于各种预测场景。

但很多初学者可能会被线性回归的核心公式吓到，那些复杂的符号和数学推导让人望而却步。

别担心，今天我们就来手把手拆解线性回归的核心公式，从零开始，一步步揭开它的神秘面纱。

一、什么是线性回归？

我们先来讲一个小故事，假如你是一位房地产经纪人，客户问你：

“我有一套100平方米的房子，大概能卖多少钱？”。

这时，你应该如何回答呢？总不能凭空猜测吧。

图1. 房价预测

这时候，线性回归就能派上大用场啦！

通过分析历史房价数据，找出房屋面积与房价之间的线性关系，你就能预测出100平方米房子的大致价格了。

线性回归不仅在房地产领域大显身手，还在金融、医疗、市场营销等众多领域发挥着重要作用。

比如，银行可以用它预测贷款违约率，医生可以用它预测患者的康复时间，电商运营人员可以用它预测销售额。

1.1 线性回归的定义

线性回归是一种通过建立线性关系来预测目标变量的方法。

简单来说，就是找到一条直线，让这条直线尽可能地“贴合”数据点。

图2. 房屋面积与房价的关系

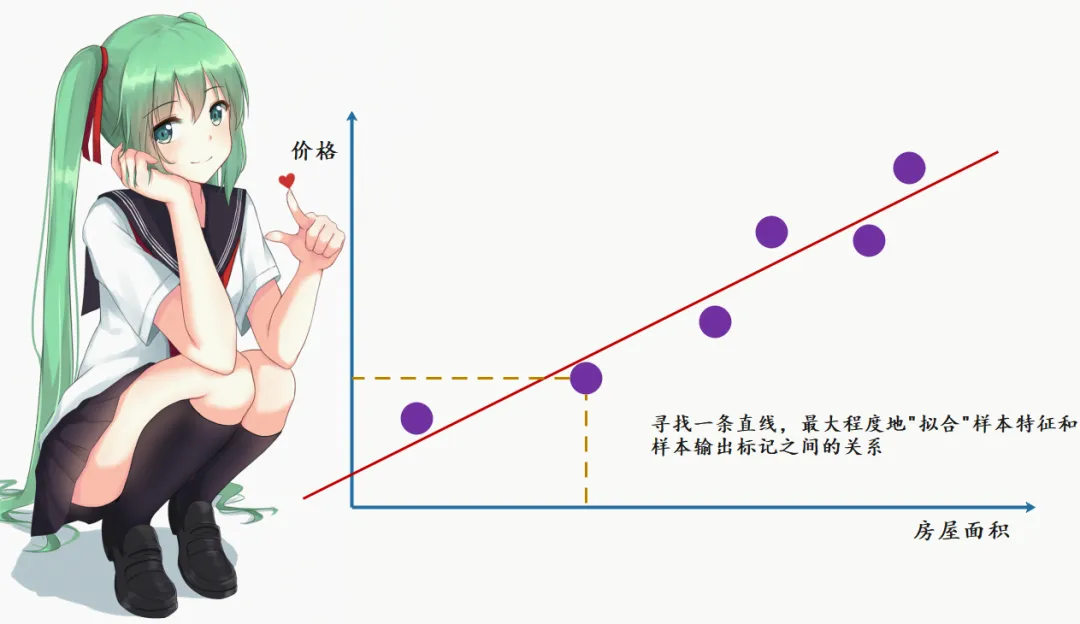
比如，我们用散点图表示房屋面积（自变量）与房价（因变量）的关系。

线性回归的目标就是找到一条直线，让这条直线与散点的距离尽可能小。

1.2 关键术语解释

🕵️ 因变量（目标变量）：我们要预测的变量，比如房价。

🕵️ 自变量（特征变量）：用来预测因变量的变量，比如房屋面积。

🕵️ 拟合直线：线性回归找到的那条“最佳”直线，用来表示自变量与因变量之间的关系。

图3. 线性回归的假设

另外，线性回归还有一些基本假设，这些假设保证了模型的有效性：

独立性：每个数据点之间是独立的，没有相互影响。
线性关系：自变量与因变量之间存在线性关系。
同方差性：误差项的方差是恒定的。
正态分布：误差项服从正态分布。

这些假设听起来有点抽象，但其实很好理解。

比如，独立性就好比你抛硬币，每次抛的结果都是独立的，不会受到之前抛的结果影响。线性关系就好比你走路，走得越远，离起点的距离就越远，这是一个线性的关系。

二、LR核心公式拆解

线性回归的核心公式是这样的：

$\beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n + \epsilon$

看起来有点复杂，别急，我们逐项解释一下：

$y$ 是我们要预测的因变量，比如房价。
$β0\beta_0$ 是截距，也就是当所有自变量都为0时，因变量的值。
$β1,β2,…,βn\beta_1, \beta_2, \ldots, \beta_n$ 是系数，表示每个自变量对因变量的影响程度。
$x1,x2,…,xnx_1, x_2, \ldots, x_n$ 是自变量，比如房屋面积、房间数量等。
$ϵ\epsilon$ 是误差项，表示模型无法解释的部分。

图4. 线性回归模型

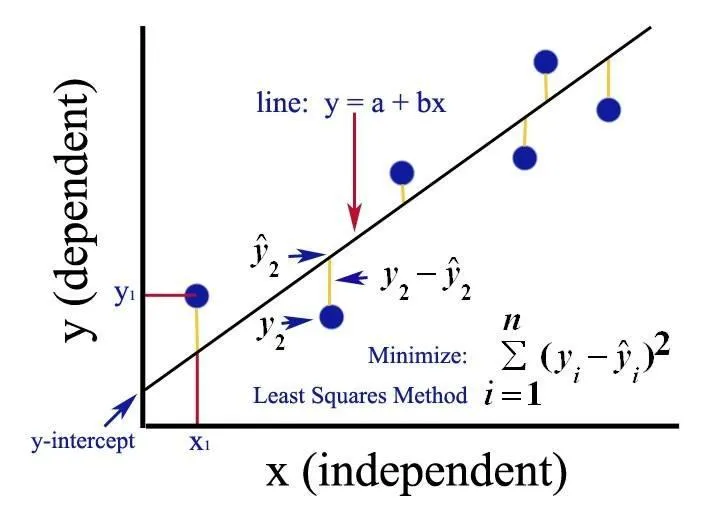
线性回归的目标是找到一条最佳拟合直线，让这条直线与数据点的距离尽可能小。这里用到的方法叫最小二乘法，它的基本思想是：最小化误差平方和。

假设我们有一组数据点 $x_i, y_i)$ ，拟合直线的预测值为 $y^i\hat{y}_i$ ，那么误差就是 $yi−y^iy_i - \hat{y}_i$ 。最小二乘法的目标是让所有误差的平方和最小，即：

$min⁡∑i=1n(yi−y^i)2\min \sum_{i=1}^{n}(y_i - \hat{y}_i)^2$

我们用一个简单的例子来说明。假设我们只有两个数据点：(1, 2) 和 (2, 3)。我们尝试用一条直线 $\beta_0 + \beta_1$ 来拟合它们。通过计算误差平方和，我们可以找到最优的 $β0\beta_0$ 和 $β1\beta_1$ 。

三、LR数学公式推导

接下来，我将详细推导线性回归的核心公式，特别是最小二乘法的推导过程。

这个过程会涉及一些数学知识，但我会尽量讲解得通俗易懂。

3.1 问题、误差定义

假设我们有一组数据点 $x_i, y_i)$ ，其中 $x_i$ 是自变量（特征）， $y_i$ 是因变量（目标值）。我们的目标是找到一个线性模型：

$\beta_0 + \beta_1x$

使得这个模型能够尽可能好地拟合数据。

为了衡量模型拟合的好坏，我们需要定义一个误差函数。误差函数通常选择误差平方和（SSE，Sum of Squared Errors），即：

$SSE=∑i=1n(yi−y^i)2SSE = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2$

其中， $y^i\hat{y}_i$ 是模型的预测值，即：

$y^i=β0+β1xi\hat{y}_i = \beta_0 + \beta_1x_i$

因此，误差平方和可以写成：

$\sum_{i=1}^{n}(y_i - (\beta_0 + \beta_1x_i))^2$

3.2 最小化SSE

为了找到最优的 $β0\beta_0$ 和 $β1\beta_1$ ，我们需要最小化误差平方和 SSE。

这是一个优化问题，可以通过求导并令导数为零来解决。

1、对 $β0\beta_0$ 求导：

$∂SSE∂β0=∂∂β0∑i=1n(yi−β0−β1xi)2\frac{\partial SSE}{\partial \beta_0} = \frac{\partial}{\partial \beta_0} \sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i)^2$

逐项求导：

$∂∂β0(yi−β0−β1xi)2=−2(yi−β0−β1xi)\frac{\partial}{\partial \beta_0}(y_i - \beta_0 - \beta_1x_i)^2 = -2(y_i - \beta_0 - \beta_1x_i)$

因此：

$∂SSE∂β0=−2∑i=1n(yi−β0−β1xi)\frac{\partial SSE}{\partial \beta_0} = -2 \sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i)$

令导数为零：

$\sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i) = 0$

简化得：

$∑i=1n(yi−β0−β1xi)=0\sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i) = 0$

2、对 $β1\beta_1$ 求导：

$∂SSE∂β1=∂∂β1∑i=1n(yi−β0−β1xi)2\frac{\partial SSE}{\partial \beta_1} = \frac{\partial}{\partial \beta_1} \sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i)^2$

逐项求导：

$∂∂β1(yi−β0−β1xi)2=−2xi(yi−β0−β1xi)\frac{\partial}{\partial \beta_1}(y_i - \beta_0 - \beta_1x_i)^2 = -2x_i(y_i - \beta_0 - \beta_1x_i)$

因此：

$∂SSE∂β1=−2∑i=1nxi(yi−β0−β1xi)\frac{\partial SSE}{\partial \beta_1} = -2 \sum_{i=1}^{n}x_i(y_i - \beta_0 - \beta_1x_i)$

令导数为零：

$\sum_{i=1}^{n}x_i(y_i - \beta_0 - \beta_1x_i) = 0$

简化得：

$∑i=1nxi(yi−β0−β1xi)=0\sum_{i=1}^{n}x_i(y_i - \beta_0 - \beta_1x_i) = 0$

3.3 求解方程组

现在我们得到了两个方程：

$∑i=1n(yi−β0−β1xi)=0\sum_{i=1}^{n}(y_i - \beta_0 - \beta_1x_i) = 0$
$∑i=1nxi(yi−β0−β1xi)=0\sum_{i=1}^{n}x_i(y_i - \beta_0 - \beta_1x_i) = 0$

我们可以通过一些代数变换来解这两个方程。

方程1：

$∑i=1nyi−∑i=1nβ0−∑i=1nβ1xi=0\sum_{i=1}^{n}y_i - \sum_{i=1}^{n}\beta_0 - \sum_{i=1}^{n}\beta_1x_i = 0$

因为 $β0\beta_0$ 和 $β1\beta_1$ 是常数，所以：

$∑i=1nyi−nβ0−β1∑i=1nxi=0\sum_{i=1}^{n}y_i - n\beta_0 - \beta_1 \sum_{i=1}^{n}x_i = 0$

解得：

$β0=1n∑i=1nyi−β11n∑i=1nxi\beta_0 = \frac{1}{n} \sum_{i=1}^{n}y_i - \beta_1 \frac{1}{n} \sum_{i=1}^{n}x_i$

记 $yˉ=1n∑i=1nyi\bar{y} = \frac{1}{n} \sum_{i=1}^{n}y_i$ 和 $xˉ=1n∑i=1nxi\bar{x} = \frac{1}{n} \sum_{i=1}^{n}x_i$ ，则：

$β0=yˉ−β1xˉ\beta_0 = \bar{y} - \beta_1 \bar{x}$

方程2：

$∑i=1nxiyi−β0∑i=1nxi−β1∑i=1nxi2=0\sum_{i=1}^{n}x_iy_i - \beta_0 \sum_{i=1}^{n}x_i - \beta_1 \sum_{i=1}^{n}x_i^2 = 0$

将 $β0=yˉ−β1xˉ\beta_0 = \bar{y} - \beta_1 \bar{x}$ 代入：

$∑i=1nxiyi−(yˉ−β1xˉ)∑i=1nxi−β1∑i=1nxi2=0\sum_{i=1}^{n}x_iy_i - (\bar{y} - \beta_1 \bar{x}) \sum_{i=1}^{n}x_i - \beta_1 \sum_{i=1}^{n}x_i^2 = 0$

整理得：

$∑i=1nxiyi−yˉ∑i=1nxi+β1xˉ∑i=1nxi−β1∑i=1nxi2=0\sum_{i=1}^{n}x_iy_i - \bar{y} \sum_{i=1}^{n}x_i + \beta_1 \bar{x} \sum_{i=1}^{n}x_i - \beta_1 \sum_{i=1}^{n}x_i^2 = 0$

提取 $β1\beta_1$ ：

$∑i=1nxiyi−yˉ∑i=1nxi=β1(∑i=1nxi2−xˉ∑i=1nxi)\sum_{i=1}^{n}x_iy_i - \bar{y} \sum_{i=1}^{n}x_i = \beta_1 \left( \sum_{i=1}^{n}x_i^2 - \bar{x} \sum_{i=1}^{n}x_i \right)$

解得：

$β1=∑i=1nxiyi−yˉ∑i=1nxi∑i=1nxi2−xˉ∑i=1nxi\beta_1 = \frac{\sum_{i=1}^{n}x_iy_i - \bar{y} \sum_{i=1}^{n}x_i}{\sum_{i=1}^{n}x_i^2 - \bar{x} \sum_{i=1}^{n}x_i}$