手把手带你推导“Ridge回归”核心公式

在机器学习中，岭回归（Ridge Regression）是一种经典的线性回归改进方法，它通过引入正则化项来解决线性回归中可能出现的过拟合问题。

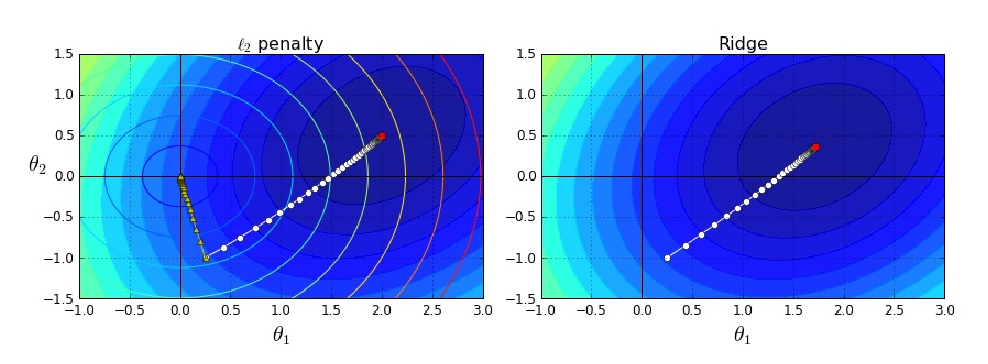
接下来，我们将详细推导岭回归的核心公式，帮助你深入理解其数学原理。

一、岭回归的基础原理

在推导“岭回归”数学公式之前，我们先回顾一下线性回归的基本概念。

线性回归的目标是找到一个权重向量 $\omega$，使得预测值 ${\omega }^T{x}_i$ 与真实值 $y_i$ 之间的平方误差最小。

图1. 线性回归原理

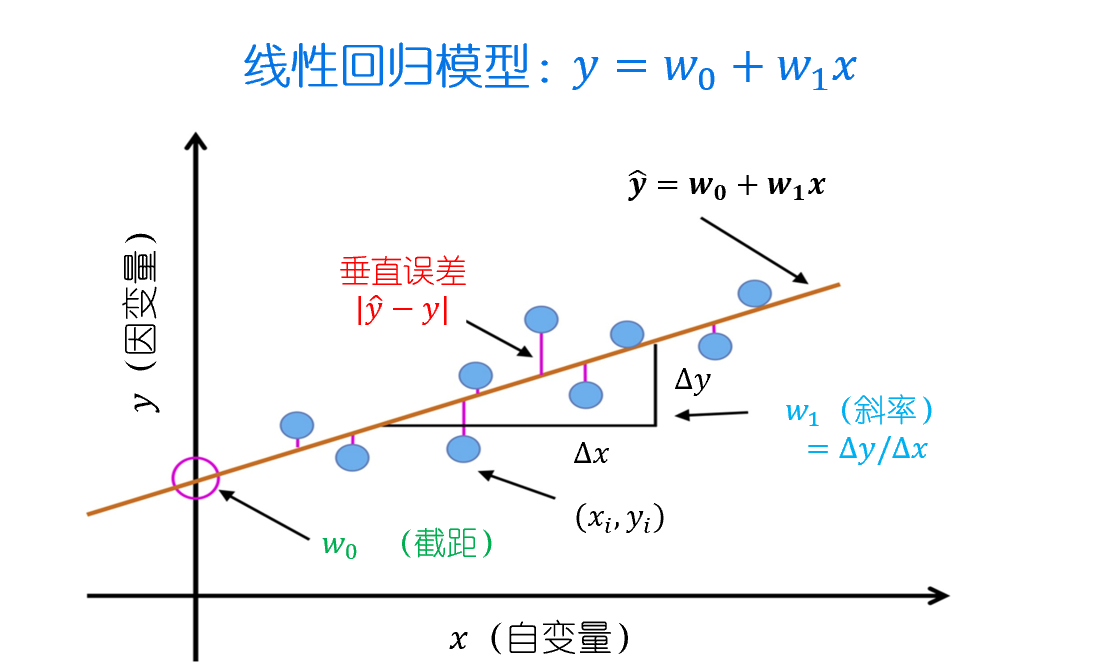
用数学公式表示就是：
$$J(\omega )=\sum _{i=1}^n(y_i-{\omega }^T{x}_i{)}^2$$
其中，$y_i$ 是目标值，$x_i$ 是特征向量，$\omega$ 是权重向量。

用矩阵形式表示，目标函数可以写成：

$$J(W)=(Y-XW{)}^T(Y-XW)$$

其中，$Y$ 是目标值向量，$X$ 是特征矩阵，$W$ 是特征矩阵。

---

岭回归的核心思想是在最小二乘法的基础上引入一个正则化项，对模型的权重进行惩罚，使其不会过大，从而降低模型的复杂度。

图2. 岭回归原理

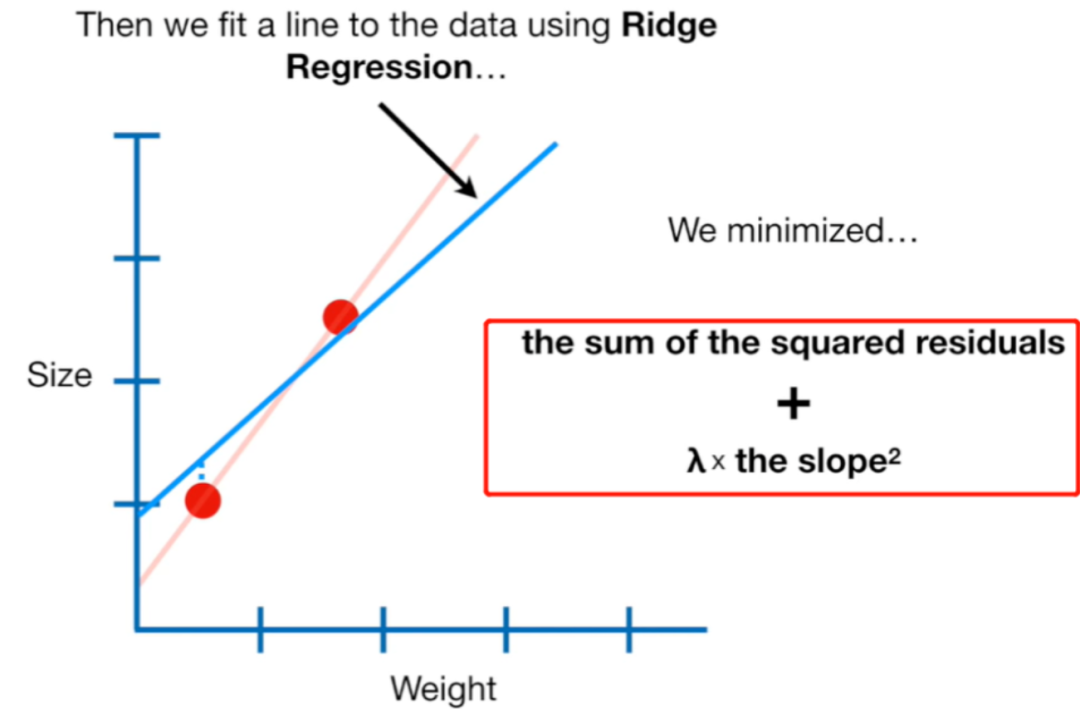
岭回归的目标函数可以表示为：
$$J(\omega )=\sum _{i=1}^n(y_i-{\omega }^T{x}_{}$$