卷积运算的魅力：卷积神经网络的核心数学原理

在当今数字化时代，人工智能技术如雨后春笋般蓬勃发展，而卷积神经网络（CNN）作为其中的佼佼者，广泛应用于图像识别、语音处理等领域。

但你知道吗？这一切的背后都离不开卷积运算这一强大的数学工具。

今天，就让我们一起深入探索卷积神经网络的数学原理，领略卷积运算的独特魅力。

一、卷积运算的定义

在数学中，卷积是一种积分运算。它将两个函数（或序列）结合在一起，生成一个新的函数（或序列）。

而在卷积神经网络中，这两个函数则分别表示输入信号（比如图像）和卷积核（也称为滤波器）。

假设输入信号为 $f(x)$，卷积核为 $g(x)$，那么它们的卷积 $h(x)$ 可以表示为：
$$h(x)=(f\ast g)(x)=\sum _{k=-\infty }^{\infty }f(k)\cdot g(x-k)$$
式中$\ast$表示卷积操作。

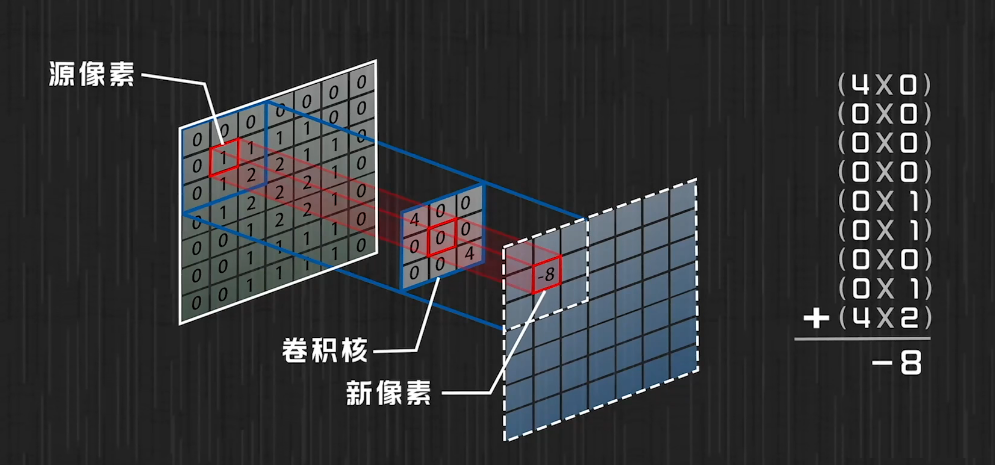
这个公式虽然看起来有点复杂，但它的本质就是将卷积核在输入信号上滑动，每次滑动后计算对应位置的加权和。

图1. 卷积运算示意图

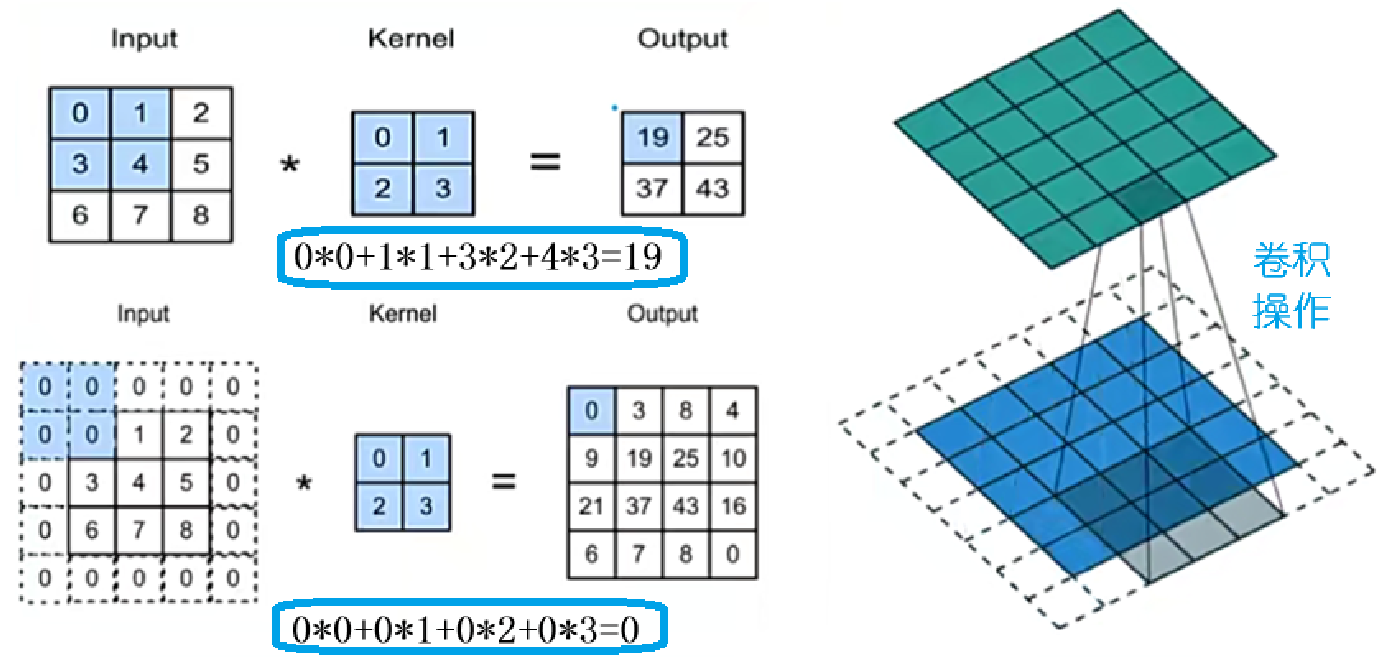
简单来说，卷积运算就像是用一个小窗口（卷积核）在图像上滑动（卷积），通过计算窗口内像素与卷积核对应元素的乘积之和，得到新的特征值。

这个过程就像是用一个“探测器”在图像中寻找特定的模式。

举个简单的例子，假设我们有一个二维的图像矩阵和一个卷积核矩阵。

卷积核在图像上逐像素移动，每到一个位置，就将卷积核与图像对应位置的像素值相乘，然后将所有乘积相加，得到的结果就构成了新的特征图中的一个像素值。

图2. 局部特征提取

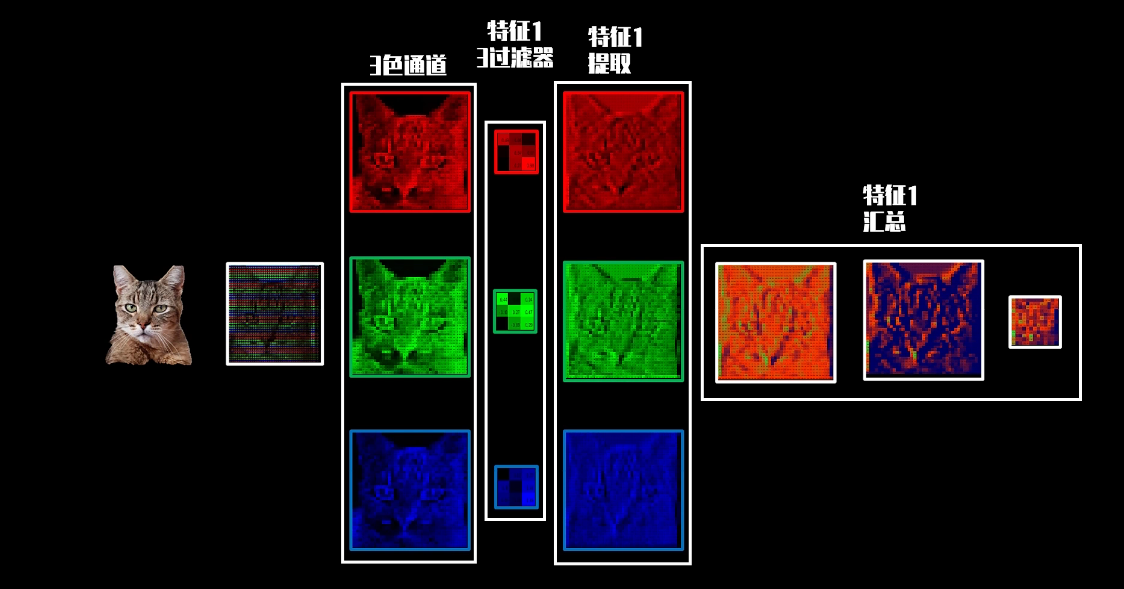
通过这种方式，卷积运算能够提取图像中的局部特征，比如边缘、纹理等。

---

卷积运算的两大重要性质：线性性质和平移不变性质。

1.1 线性性质

卷积运算满足线性叠加原理，具体包括加法性质和数乘性质：

• 加法性质：如果将两个图像分别与同一个卷积核进行卷积，然后将结果相加，等同于先将两个图像相加再进行卷积。
  $$(f(t)+g(t))\ast h($$