手把手带你推导“软间隔SVM”核心公式

在机器学习中，数据往往存在噪声和异常值，这使得硬间隔SVM（即要求所有数据点都正确分类）难以适用。

因此，软间隔SVM应运而生，它允许一些数据点违反分类规则，从而提高了模型的泛化能力。

今天，我们将从头开始，一步步推导软间隔SVM的数学原理。

一、SVM的基本原理

支持向量机（SVM）是一种用于分类和回归的监督学习算法。它的核心思想是找到一个超平面，将不同类别的数据点分隔开，同时最大化间隔。

图1. 最大化间隔

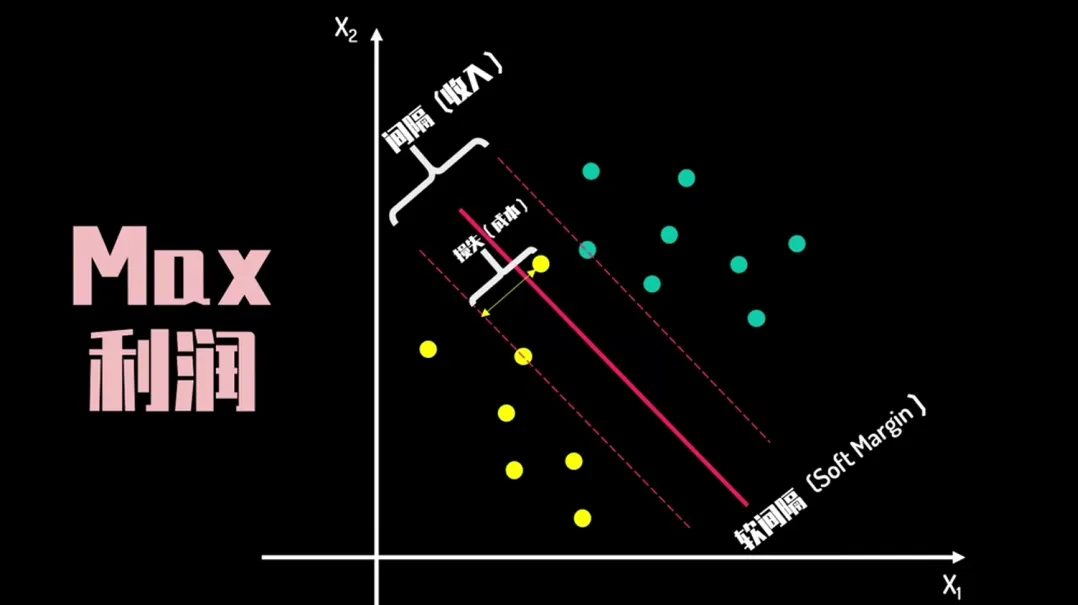
而SVM 的关键在于如何定义和最大化这个间隔。

1.1 硬间隔SVM

在介绍软间隔SVM之前，我们先回顾一下硬间隔SVM的基本原理。

假设我们有一个线性可分的数据集，每个数据点 $x_i$ 都有一个标签 $y_i$，其中 yi∈{ −1,1}y_i \in \{-1, 1\}yi​∈{ −1,1}。

我们的目标是找到一个超平面，能够将这两类数据完全分开。

超平面可以用以下方程表示：

$$\mathbf{w}\cdot \mathbf{x}+b=0$$

其中，$\mathbf{w}$ 是超平面的法向量，$b$ 是偏置项。对于任意一个数据点 ${\mathbf{x}}_i$，它到超平面的距离可以表示为：

$$\text{距离}=\frac{|\mathbf{w}\cdot {\mathbf{x}}_i+b|}{\Vert \mathbf{w}\Vert }$$

为了最大化这个距离，我们需要最小化 $\Vert \mathbf{w}\Vert$。因此，硬间隔SVM的优化问题可以表示为：

$$\begin{gathered} \underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2 \\ \text{subject to}{y}_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)\ge 1,\forall i \end{gathered}$$

这个优化问题是一个凸二次规划问题，可以通过拉格朗日乘子法求解。

1.2 软间隔SVM

在实际应用中，数据往往不是线性可分的，或者存在噪声和异常值。

硬间隔SVM在这种情况下会遇到问题，因为它要求所有数据点都满足分类规则。

软间隔SVM通过引入松弛变量 ${\xi }_i$ 来允许一些数据点违反分类规则，从而提高模型的泛化能力。

软间隔SVM的优化问题可以表示为：

$$\underset{\mathbf{w},b,\xi }{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^{}$$