手把手带你推导“硬间隔SVM”核心公式

在机器学习中，支持向量机（SVM）是一种非常强大的分类算法。它不仅能够有效地处理高维数据，还能在许多实际应用中取得优异的性能。

今天，我们就来深入探讨支持向量机的硬间隔版本，从原理到公式，一步步推导，让你彻底理解这个算法的精髓。

一、为什么需要SVM

在分类问题中，我们的目标是找到一个决策边界，将不同类别的数据分开。

假设我们有一组二维数据，其中每个数据点都有一个标签，表示它属于类别 A 或类别 B。最直观的想法是画一条直线，将这两类数据分开。

图1. 支持向量机示意图

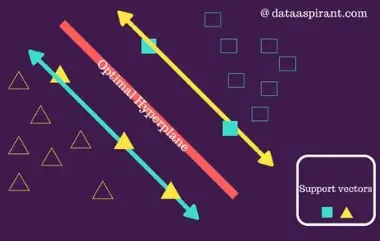
然而，很多时候，数据并不是线性可分的，或者即使可以线性分开，也可能存在多种选择。

那么，我们应该如何选择最优的决策边界呢？

支持向量机（SVM）正是为了解决这个问题而诞生的。

它不仅能够找到一个能够正确分类的决策边界，还能最大化边界与数据点之间的间隔，从而提高模型的泛化能力。

接下来，我们就来详细了解一下 SVM 的原理和推导过程。

二、SVM的基本概念

在推导SVM之前，我们先来了解一些基本概念：

2.1 线性可分

假设我们有一组线性可分的数据，即存在一条直线（在二维空间中）或一个超平面（在高维空间中），能够将不同类别的数据完全分开。

我们的目标是找到这样一个决策边界，使得它不仅能够正确分类，还能最大化边界与最近的数据点之间的间隔。

这些最近的数据点被称为支持向量。

2.2 决策函数

在 SVM 中，决策边界通常表示为一个线性函数：

$$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$$

其中，$\mathbf{w}$ 是权重向量，$\mathbf{x}$ 是输入特征向量，$b$ 是偏置项。对于一个数据点 ${\mathbf{x}}_i$，如果 $f({\mathbf{x}}_i)>0$，则它属于类别 1；如果 $f({\mathbf{x}}_i)<0$，则它属于类别 -1。

2.3 间隔（Margin）

间隔是指决策边界与最近的数据点之间的距离。在 SVM 中，我们希望最大化这个间隔。对于一个数据点 ${\mathbf{x}}_i$，它到决策边界的距离可以表示为：

$$\text{Distance}=\frac{|{\mathbf{w}}^T{\mathbf{x}}_i+b|}{\Vert \mathbf{w}\Vert }$$

由于我们希望最大化间隔，因此需要最大化这个距离。然而，为了简化问题，我们通常最大化间隔的倒数，即最小化 $\Vert \mathbf{w}\Vert$。

图2. 最大化间隔

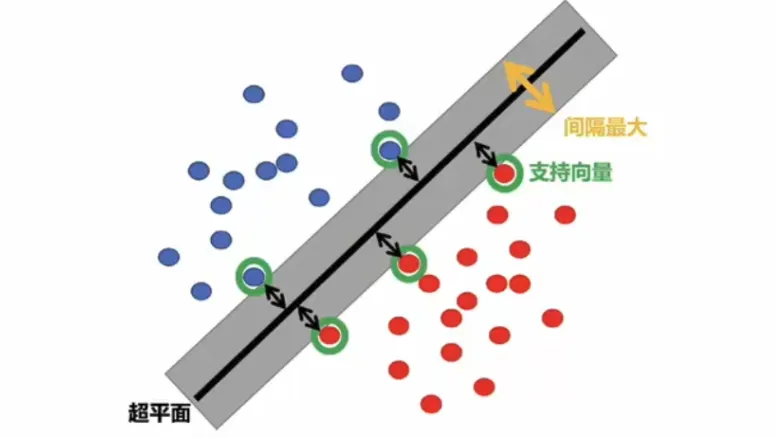
在支持向量机（SVM）的理论框架中，硬间隔和软间隔是两种不同的分类策略：

• 硬间隔支持向量机要求数据完全线性可分且间隔最大化。

• 软间隔支持向量机则通过引入松弛变量和惩罚参数，允许部分数据违反间隔约束，以提高模型的泛化能力。

接下来，我们将进一步探讨硬间隔支持向量机的数学推导过程。

三、SVM硬间隔数学推导

接下来，我们将进一步推导硬间隔SVM的核心公式。

3.1 优化目标

硬间隔 SVM 的目标是在数据完全线性可分的情况下，找到一个最优的分界线，使得两类数据之间的间隔最大化。

这个间隔是由最近的数据点（支持向量）决定的，这些数据点恰好位于分界线的两侧边界上。

假设数据集为 { ( x i , y i ) } i = 1 n \{(x_i, y_i)\}_{i=1}^n { (xi​