
在神经网络的世界里,反向传播算法(Backpropagation)堪称“幕后英雄”,尽管它并不直接参与神经网络的前向传播(即从输入到输出的计算过程),但其在训练阶段的作用不可或缺。
我们可以把神经网络想象成一个学习机器,它需要通过大量的数据来学习如何完成任务,比如识别照片里的动物或者翻译语言。
反向传播算法就像是这个学习机器的“教练”,它告诉神经网络在学习过程中哪里做得好,哪里需要改进。今天,就让我们深入探讨反向传播算法的数学原理,揭开它神秘的面纱。
一、前向传播与反向传播
在了解反向传播之前,我们先来回顾一下神经网络的前向传播。
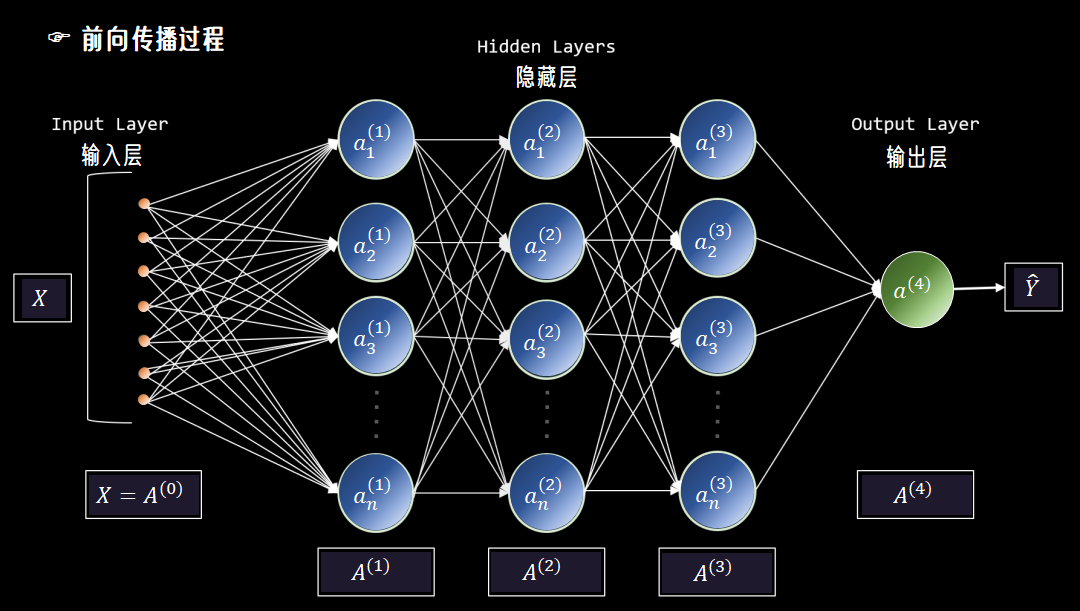
神经网络结构主要由输入层、隐藏层和输出层组成,数据从输入层进入。
经过每一层的神经元进行加权求和、激活函数处理,最终到达输出层,得到预测结果。
这个过程就像是水流从上游流向下游,我们称之为前向传播。

然而,仅仅有前向传播是不够的。因为神经网络的初始权重是随机初始化的,所以它在第一次前向传播时产生的预测结果往往是不准确的。
为了提高预测的准确性,我们需要对神经网络进行训练,而训练的核心就是反向传播算法。
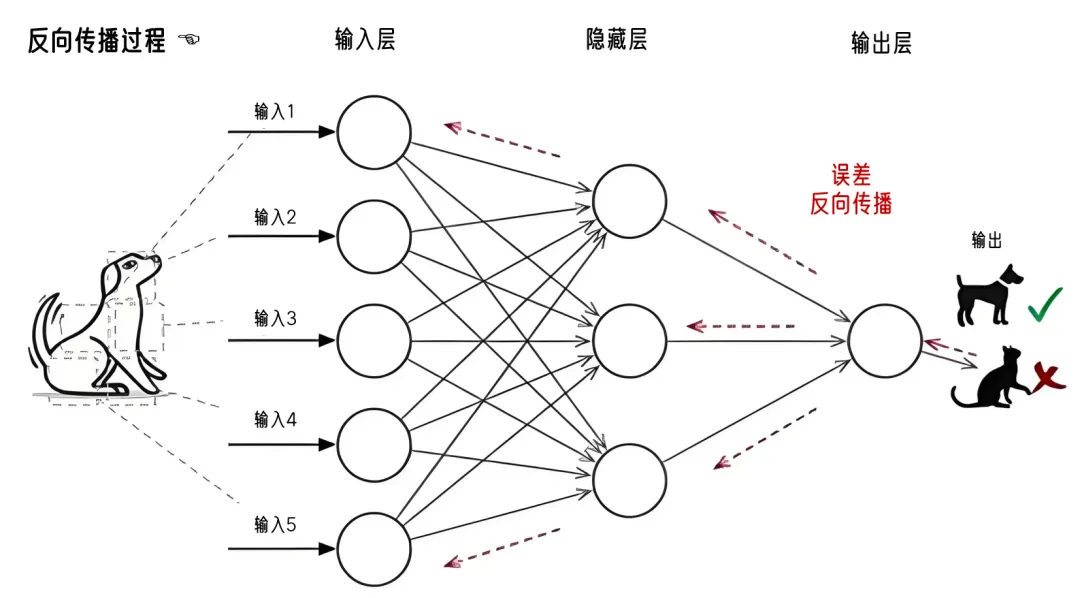
反向传播算法的核心思想是通过计算损失函数对每个权重的梯度,来调整权重,使损失函数的值逐渐减小。
损失函数是衡量预测值与真实值之间差异的函数,它的值越小,说明神经网络的预测越准确。
反向传播的过程是从输出层开始,沿着神经网络的层次反向传播,逐层计算梯度并更新权重。
二、链式法则在反向传播中的应用
链式法则是微积分中的一个重要工具,它在反向传播算法中扮演着至关重要的角色。
链式法则的数学形式是:如果一个函数 yyy 是另一个函数 uuu 的函数,即 y=f(u)y = f(u)y=f(u),而 uuu 又是另一个变量 xxx 的函数,即 u=g(x)u = g(x)u=g(x),那么 yyy 对 xxx 的导数可以表示为:
dydx=dydu×dudx \frac{dy}{dx} = \frac{dy}{du} \times \frac{du}{dx} dxdy=dudy×dxdu
在神经网络中,每个神经元的输出是前一层神经元输出的函数,而损失函数又是最后一层神经元输出的函数。
因此,要计算损失函数对每个权重的梯度,就需要使用链式法则,将损失函数对神经元输出的导数与神经元输出对权重的导数相乘。
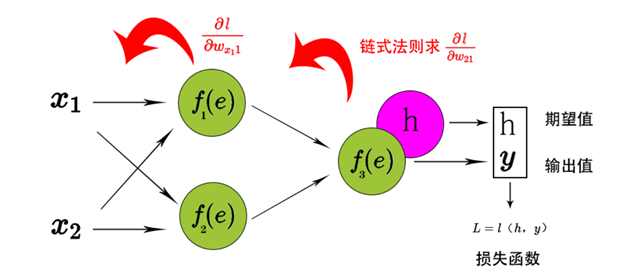
例如,假设我们有一个简单的两层神经网络,输入层有一个神经元,隐藏层有一个神经元,输出层有一个神经元。
损失函数 LLL 是输出层神经元的输出 yyy 的函数,而 yyy 是隐藏层神经元的输出 zzz 的函数,zzz 又是输入层神经元的输出 xxx 的函数。
那么,要计算损失函数 LLL 对输入层到隐藏层的权重 www 的梯度,就需要使用链式法则:
∂L∂w=∂L∂y×∂y∂z×∂z∂w \frac{\partial L}{\partial w} = \frac{\partial L}{\partial y} \times \frac{\partial y}{\partial z} \times \frac{\partial z}{\partial w} ∂w∂L=∂y∂L×∂z∂y×∂w∂z
通过链式法则,我们可以将复杂的梯度计算分解为多个简单的导数计算,从而高效地计算出每个权重的梯度。
三、反向传播算法的数学推导
为了更好地理解反向传播算法,我们可以通过一个简单的两层神经网络来推导其数学过程。
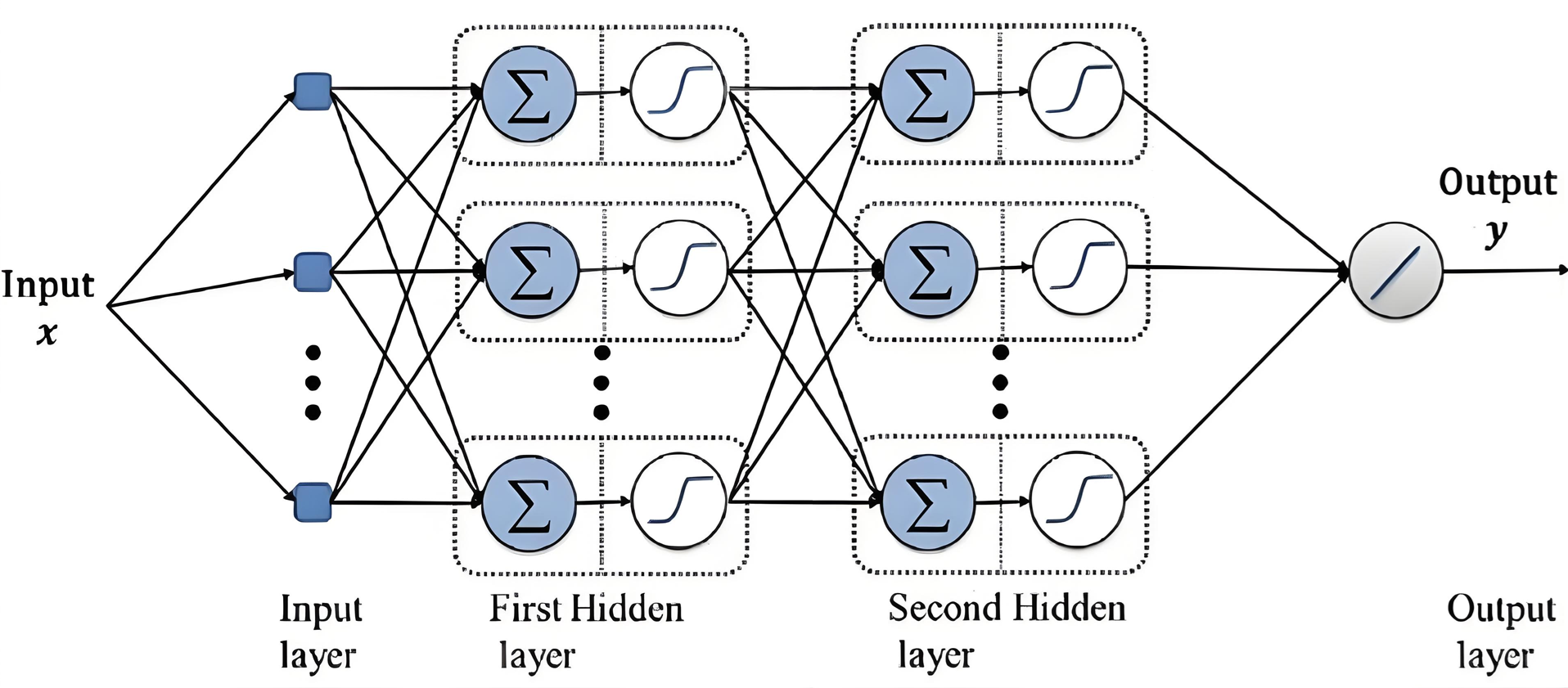
其中,隐藏层使用 Sigmoid 激活函数,输出层使用线性激活函数,损失函数采用均方误差(MSE)。
3.1 前向传播
首先,我们进行前向传播。假设输入为 xxx,隐藏层的权重为 W1W_1W1,偏置为 b1b_1b1,输出层的权重为 W2W_2W2,偏置为 b2b_2b2。
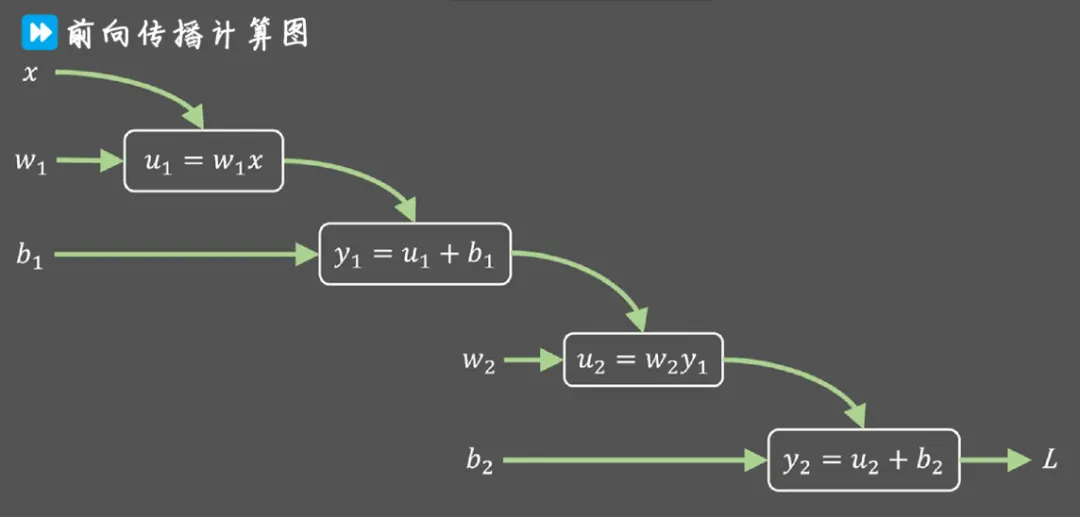
- 隐藏层的输出 zzz 和激活值 aaa 可以表示为:
z=W1x+b1 z = W_1x + b_1 z=W1x+b1
a=σ(z)=11+e−z a = \sigma(z) = \frac{1}{1 + e^{-z}} a=
 反向传播的数学原理详解
反向传播的数学原理详解





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








