在复高斯分布中,若复随机变量服从如下:
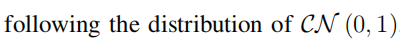
那么该随机变量的实部和虚部分别服从如下分布:

同时,实部和虚部的期望有如下结论:

循环对称复高斯随机变量,参考如下(没懂):
高斯分布及归一化、标准化、零均值化

双伽马函数:

复高斯白噪声,验证包络服从瑞利分布,包络平方服从指数分布
在复高斯分布中,若复随机变量服从如下:
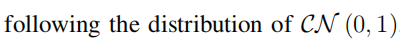
那么该随机变量的实部和虚部分别服从如下分布:

同时,实部和虚部的期望有如下结论:

循环对称复高斯随机变量,参考如下(没懂):
高斯分布及归一化、标准化、零均值化

双伽马函数:

复高斯白噪声,验证包络服从瑞利分布,包络平方服从指数分布
 6561
6561

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


