自动驾驶-动作规划1 原理

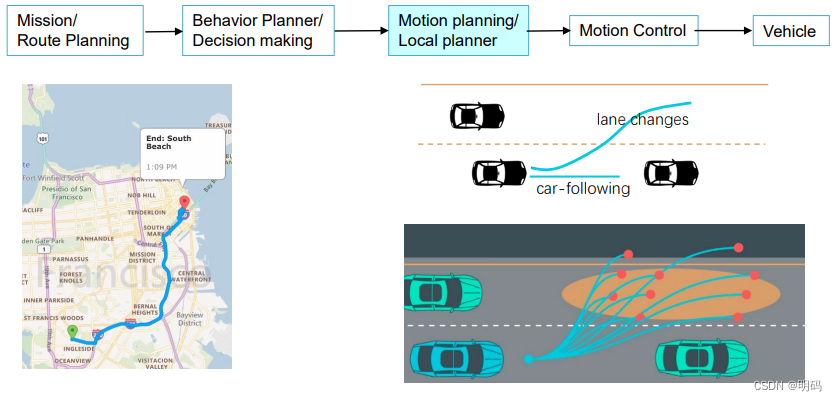
Vehicle Motion Planning/Local Planner

T： 确定一系列行动以达到指定目标

W： 搜索

• Functionality and Common method

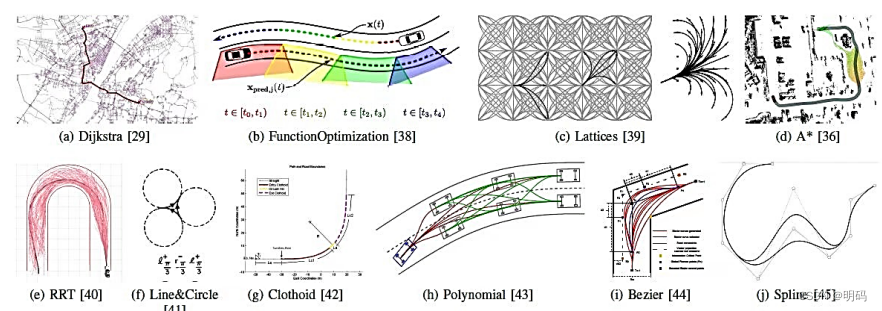
(a)Global path by Dijkastra.
(b) Trajectory optimization considering a vehicle in the other lane.
© Lattices and motion primitives. (d)Hybrid A* in DRAPA Junior. (e) RRT.
(f) Optimal path to turn the vehicle around. (g) Planning a turn from Stanford.
(h) Different motion states, planned with polynomial curves. (i) Evaluation of several Bezie curves. (j) Spline behaviour when a knot changes places
概括：

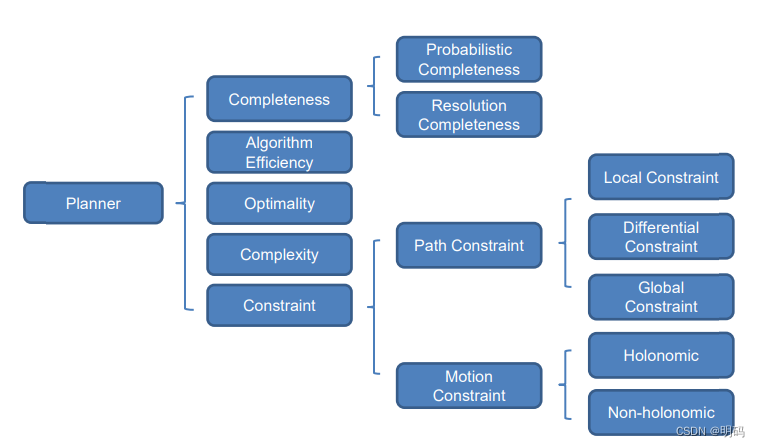
• Fundamental Concepts and Key terminology

Completeness: 只要有路；就能找到路
• Ability to find a solution if one exists,
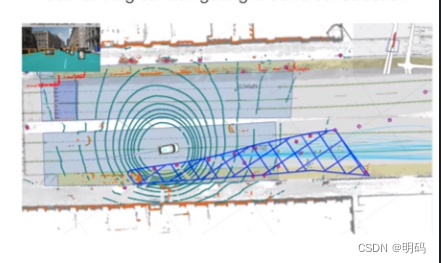
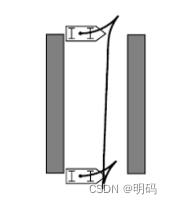
• Narrow Gap Problem Examples

Self-driving car navigating around construction

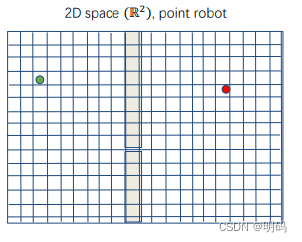
Probabilistic Completeness: 主要针对采样，如果存在路，只要有足够时间，就能找到路
Probability of finding a solution (when one exists) increases as computational time spent on the problem increases

Batch Informed Trees(BIT*)

**Resolution Completeness:**如果在状态和/或控制空间的离散化中使用足够精细的分辨率，能够找到路
Ability to find a solution if one exists AND using fine enough resolution in discretization of the state and/or control space

Algorithmic efficiency: 算法如何解决时间与输入数据大小成比例的问题，描述采用大O标记法，也就是算法中常用于描述复杂度的方法。How an algorithm solve time scales proportionally with respect to size of the input data,

Optimality:
Optimal is able to find the lowest cost solution of all possible options,
• Suboptimal of a lower cost solution exists,
• Asymptotically optimal if guaranteed to converge to the optimal solution given increasing computational time spent on the problem.

Complexity
Space dimensionality
• configuration space is a $R^3$ for rigid body. But for the multi-bodies track, bicycle mode is not accurate enough to capture all the constraints.比如柔性机器人；
 Geometric complexity
• How bounding box and bounding box interact；
• How to detect a path between polygons and interact with another obstacles；
…
There are three types of Path Constraints：
 Local Constraints
• Avoid collision with static obstacles
 Differential constraints
• Bounded curvature, limited steering angle for vehicle
 Global constraints
• Find the shortest path by A

Holonomic vs non-holonomic motion constraints
Holonomic：控制的自由度=机器人总的自由度 如全向车
Cars are non-holonomic since control throttle and steering (2 DOF), but move in 𝑆E(2) (𝑥, 𝑦, 𝜃)

Local Planning

Find higher precision “good” (near optimal w.r.t. cost function) path to execute.
where to search
质点模型->Configuration Space Parameterization Options
● Workspace (direct physical environment, traditional)

• Control Space (e.g. velocity space, see link)
• Only saves effort in simple problems
  ● Belief Space (POMDP)

How to search?

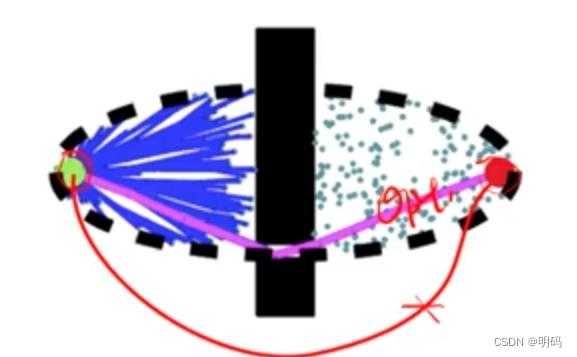
• Combinatorial methods (exact complete solution, e.g. visibility graph )
  Rarely exists to find optimal solution to complex problems 起始点连线存在障碍物，最优解往往贴着障碍物，增加了碰撞的风险
  

• Sampling-based methods
  • Deterministic (resolution complete), e.g. uniform grid or road structure graph, repeatable
  • Stochastic (probabilistic completeness), e.g. random sampling
  May need some smoothing/post-process to improve quality of solution
  

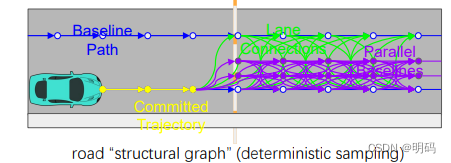
Stochastic Sampling Methods

obstacle avoidance

• 对于圆近似处理
  
• polygon
  两步
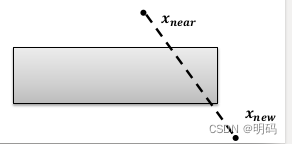
  1.如果 x_near和x_new在障碍物的同一边： 那么与障碍物没有碰撞
  2.如果不在同一边；那么判断x_new 是否在障碍物中，如果在那么一定发生碰撞
  如果不在那么需要连接两点做检查

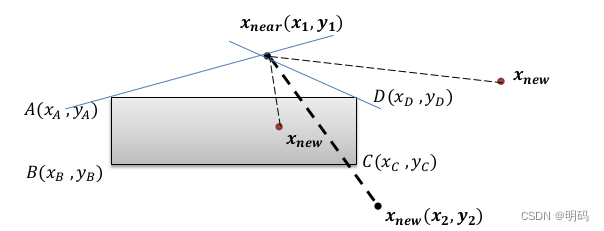
通过连接边界点线的斜率来判断

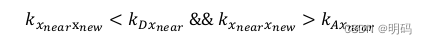
where k is the slope of line

Improvements may come through focus on any of those steps individually, e.g.:
•
Connect with edges of desirable properties

 Dubins for shortest length w/fixed turn radius 只能往前走，Dubins曲线是在满足曲率约束和规定的始端和末端的切线方向的条件下，连接两个二维平面（即X-Y平面）的最短路径
 Reeds-Shepp for forward/backward w/fixed turn radius，可以向后退
 Spline, clothoid, Bezier for continuous curvature

Reference

深蓝学院
State Space Sampling of Feasible Motions for High-Performance Mobile Robot Navigation in Complex Environments,Thomas M. Howard, Colin J. Green, and Alonzo Kelly
Frenet坐标推导过程整理