差分移动机器人的运动模型

最新推荐文章于 2025-05-18 12:58:35 发布
最新推荐文章于 2025-05-18 12:58:35 发布
阅读量5.1k 收藏 10
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 定位与导航
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_35508344/article/details/83006923
本文深入探讨了移动机器人在SLAM（Simultaneous Localization and Mapping）中里程计积分的重要性，解析了不同积分方法如欧拉法与龙格库塔法（RK2）在精度上的差异。通过对比分析，阐述了pro1里程计模型如何实现更精确的位置估计，以及其与圆弧模型的关系。此外，还介绍了diego标定方法在里程计积分中的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

转载添加链接描述

对于移动机器人来讲，由两个矩阵特别重要

//from base_link to global odom
ca  -sa  0
sa   ca  0
0    0   1
//from odom to base link
ca  sa   0
-sa ca   0
0   0    1
//两个相乘为单位矩阵，所以就是互逆

航迹推演

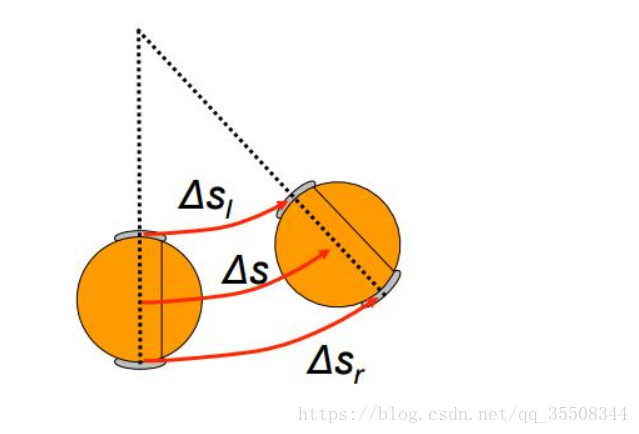
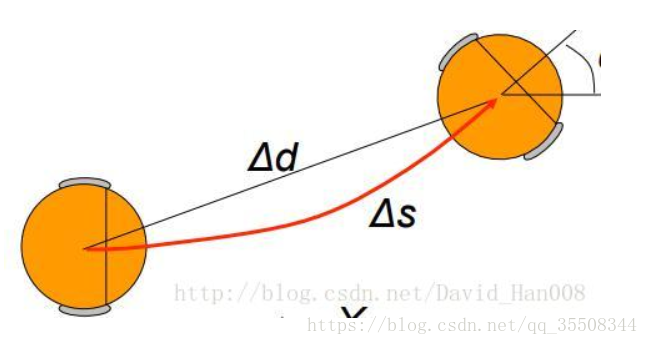
短时间内圆弧和直线近似

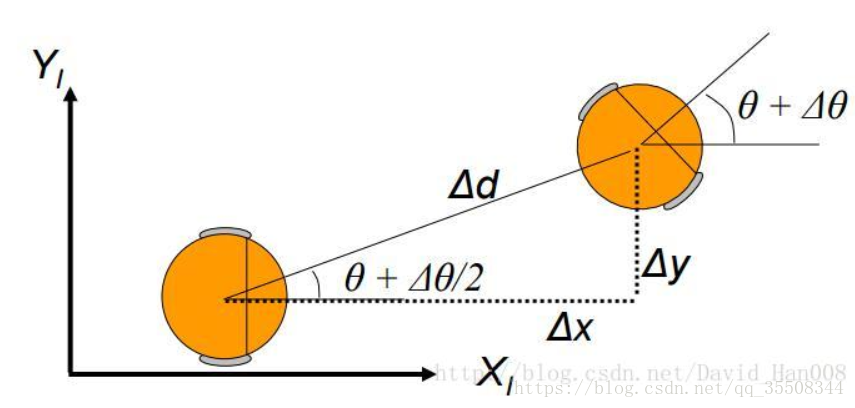
转向角和转向角一半的数学关系

参数化

速度

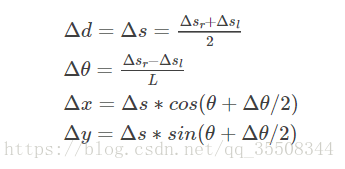
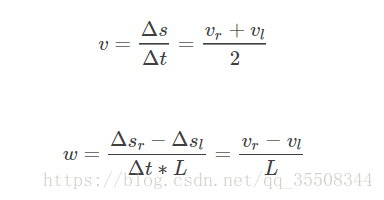
如上，在里程计积分时，
有的地方 * cos(theta ) (属于欧拉法)
有的地方 * cos(theta + 1/2 △) （属于龙格库塔法 rk2），理论上精度更高一点

模型

旷世slam
圆形轨迹
pro1里程计积分
pro1的里程计模型本质上相当于rk2, 使用位置环计算位移和角速度，delta_dis/delta_theta 求出半径，然后计算在前一个位置位移的x,y, 再积分（后一个位置做向前一个位置半径的垂线，再前一个位置x,y坐标分解）
切线，割线，圆弧模型通俗理解

标定

diego 标定
本质上标定的里程计积分中的delta x ，delta theta,

移动机器人系列1——移动机器人分类
二毛的博客
04-15 1150
1、差分类型 双轮驱动 四轮驱动 场景的机器人场景。 2、 三轮车型 3、自行车型 在电动汽车和无人驾驶车里很常见。 4、全向移动型 全向轮可以绕轮子主轴旋转，也可以绕轮子轴心旋转。 机器人的轮子左上角斜向下，右轮斜向上。 四轮转速相同，合力向左 ...
MATLAB - 移动机器人运动学方程
weixin_46300916的博客
01-18 2130
机器人状态用三元素向量表示： [x y θ]。对于给定的机器人状态x: 以米为单位的全局车辆 x 位置y: 全局车辆的 y 位置，以米为单位θ: 全局车辆航向，单位为弧度ψ: 车辆转向角，单位为弧度v: 车辆速度，单位为米/秒ω: 车辆角速度，单位为弧度/秒运动学方程中的其他变量包括r: 车轮半径，单位米: 车轮速度（弧度/秒d: 轨道宽度（米l: 轮距（米ψ: 车辆转向角，单位为弧度。
两轮差速移动机器人运动分析、建模和控制
热门推荐
启小新的博客
11-02 8万+
两轮差速运动分析及建模运动学分析三种运动状态分析函数模型仿真验证直线验证曲线验证旋转验证运动控制 运动学分析 运动特性为两轮差速驱动，其底部后方两个同构驱动轮的转动为其提供动力，前方的随动轮起支撑作用并不推动其运动，如图1两轮差速驱动示意图所示。 定义其左右驱动轮的中心分别为Wl和Wr，且对应线速度为Vl和Vr，该值可以通过电机驱动接口输出的角转速ωl，ωr2和驱动轮半径r求得，即： Vl=r⋅...
二、移动机器人的运动学分析和动力学分析
最新发布
2201_75538301的博客
05-18 376
4. 全向移动型。
差分移动机器人运动学模型
sannianyihoushuma的博客
12-01 7366
http://www.diegorobot.com/wp/?p=740&lang=zh https://blog.youkuaiyun.com/qq_16149777/article/details/73224070 https://blog.youkuaiyun.com/qq_35508344/article/details/83006923 https://blog.youkuaiyun.com/u01042243...
二 树莓派3+ROS-kinetic+mbed-二轮差分模型
kevin_chan04的博客
11-07 3208
ROS教程 二 树莓派3+ROS-kinetic+mbed/开环二轮差分模型
移动机器人动力学
qq_45443570的博客
06-12 1569
移动机器人动力学方程
（ROS）差分轮式机械臂机器人（一）模型搭建
KNIGHT_HOY的博客
01-29 3609
模型搭建 文章目录源码地址ROS版本：noetic文件结构创建功能包编写模型描述文件.xacro基本语法描述文件为显示机器人模型显示坐标系保存配置每次打开rviz并加载上次保存launch文件urdfgazebogazebo创建地图直接添加模型使用editor最后效果 本文参考了古月居的ROS入门教程 模型效果 源码地址 ROS版本：noetic 文件结构 vn_robot_description <<< config <<< launch <<<
差分驱动移动机器人的精确曲线运动规划.doc
07-11
在运动学分析方面，本文对差分驱动移动机器人的运动特性进行了分析，讨论了移动机器人的运动学模型，包括机器人的速度矢量、角速度和线速度等。 在实验方面，本文通过仿真和实际实验，证明了单曲率路径的跟踪误差...
移动机器人差分驱动控制论文
07-01
在本论文中，我们提出了一种基于脉宽调制（PWM）的移动机器人运动控制技术，该技术应用于AMiR机器人平台上，AMiR是一种自主微型机器人，专门用于群体机器人平台。该机器人采用差分驱动配置，配备了一个转向轮和一个...
差分轮式机器人模型matlab,两轮差速机器人运动学分析和控制研究
weixin_36265390的博客
03-23 3413
龙源期刊网 http://www.qikan.com.cn两轮差速机器人运动学分析和控制研究作者：王维新来源：《现代电子技术》2012年第10期摘 要：对两轮差速机器人的运动控制进行分析，建立了输入/输出量之间的函数隶属关系，在建立轮式机器人的运动学模型和动力学模型基础上，为实际研究提供可行性指导和理论依据。同时为博创平台的差速机器人运动控制提出新的思路，即基于模糊控制的机器人路径跟踪。将增量式P...
地面移动机器人越障动力学建模与分析.pdf
09-15
地面移动机器人越障动力学建模与分析pdf,地面移动机器人越障动力学建模与分析
差分轮机器人的设计
09-01
差分轮机器人的设计
基于动力学模型的轮式移动机器人电机控制
11-27
基于动力学模型的轮式移动机器人电机控制,算法
多移动机器人系列（一）-移动机器人运动学模型
qq_45097839的博客
02-15 1881
移动机器人是机器人的一个重要的分支，在无人驾驶、太空探索、海洋勘探和医疗服务等领域得到了广泛的使用。其中轮式移动机器人是一个重要的分支，轮式移动机器人又可以根据驱动方式的不同分为阿克曼结构，两轮差速结构和麦克纳姆轮结构等。随着相关技术的迅猛发展，移动机器人的性能得到了极大地提高。对于一些具有时间分布和空间分布的任务，单个移动机器人具有一定的局限性。通过多个移动机器人相互之间的协作，在处理一些时空分布的任务上表现出极大地优势，多移动机器人已经成为为移动机器人发展的热门领域之一。
差动驱动机器人轨迹-CoCube
zhangrelay的专栏
12-06 2598
轨迹博客：玫瑰线轨迹如何规划？（desmos+ROS2+turtlesim+……）ROS1云课→23turtlesim绘制小结（数学和编程）如上所涉及的机器人假定模型都是差动驱动机器人。许多移动机器人使用一种称为差动驱动的驱动机构。它由安装在公共轴上的两个驱动轮组成，每个轮可以独立地向前或向后驱动。图1:差动驱动运动学-Dudek和Jenkin《移动机器人的计算原理》机器人旋转的点被称为ICC -瞬时曲率中心通过改变两个轮子的速度，可以改变机器人的轨迹。这类驱动器有三个有趣的例子：注意，差动驱动机器人不能沿
移动机器人运动模型（两轮、四轮、麦克纳姆轮和概率运动）
qq_46067306的博客
07-08 2万+
运动机器人通常可以采用轮式和足式进行移动，通过电机驱动轮子移动机器人即轮式机器人，通过仿生式的多足关节移动机器人即多足机器人。由于多足机器人控制非常复杂，所以商业应用较多的是轮式机器人。轮式机器人底盘按照转向方式的不同，可以分为；两轮差速模型，四轮差速模型、阿克曼模型、全向模型。日常生活中，常见的就是四轮差速模型，在做小车时通常会用到麦克纳姆轮，而两轮差速模型是最基础最简单的底盘运动模型，这里就对这三种着重介绍一下。............
移动机器人运动模型
weixin_48334986的博客
08-10 1419
unicycleKinematics 创建了一个独轮车模型，用于模拟类似汽车的简化车辆动力学。车辆状态被定义为一个三元素向量 [x y theta]，其中全局 xy 位置以米为单位，车辆航向角 theta 以弧度为单位。该模型近似于一个具有给定车轮半径（WheelRadius）的独轮车，它可以根据航向角（theta）原地旋转。要计算模型的时间导数状态，可使用导数函数，输入指令和机器人当前状态。创建语法描述。
常见移动机器人运动学模型总结
qq_19598969的博客
06-16 5660
文末有彩蛋【原文及其原文中所涉及文章的PDF（共9篇）免费下载】混沌无形混沌系统是世界本质，无形之中存在规律。机器人智能化发展从线性过渡到混沌，本号将分享机器人全栈技术（感知、规划、控制；软件、机械、硬件等）。43篇原创内容公众号01引言笔者已经对常见的移动机器人的运动学模型做了详尽的分析（感兴趣的读者可以在公众号中查看），本文仅对之前的分析做一个小总结。常见的移动机器人如两轮差速驱动机器人、麦轮移动平台等，被应用于各种场景。笔者的逻辑是：由于不同实际场景的不同需求，促使工程师们绞尽脑汁从轮子构造、本体构型
差分轮移动机器人模型预测控制MPC
03-16
### 差分轮移动机器人模型预测控制（MPC）实现方法 #### 1. 模型预测控制基本原理 模型预测控制是一种基于优化的方法，通过在线解决有限时间范围内的最优控制问题来计算当前时刻的最佳输入序列。对于差分轮移动机器人，其核心在于构建合适的动态模型并将其转化为可求解的优化问题。 在轨迹跟踪应用中，MPC 的建模可以分为两类：基于运动学的状态方程建模和基于动力学的状态方程建模[^2]。由于差分轮移动机器人通常运行在较低速度下，因此更常用的是基于运动学的建模方式。 --- #### 2. 双轮差速运动学模型 双轮差速移动机器人的运动可以用如下连续时间状态空间表示： \[ \begin{aligned} \dot{x} &= v \cos(\theta), \\ \dot{y} &= v \sin(\theta), \\ \dot{\theta} &= \frac{v}{L} \tan(\phi), \end{aligned} \] 其中 \(x\) 和 \(y\) 表示机器人中心的位置坐标，\(\theta\) 是朝向角，\(v\) 是线速度，\(\phi\) 是车轮转向角，\(L\) 是轴距长度。为了简化控制器设计，可以通过假设或近似处理将该非线性模型线性化[^1]。 --- #### 3. 状态方程的线性化与离散化 通过对上述非线性模型进行泰勒级数展开，并忽略高阶项，得到局部线性化的状态转移矩阵形式： \[ \Delta X_{k+1} = A_k \Delta X_k + B_k \Delta U_k, \] 其中， - \(\Delta X_k = [e_x, e_y, e_\theta]^T\) 表示当前位置误差； - \(\Delta U_k = [\Delta v, \Delta w]^T\) 表示控制增量； - \(A_k\) 和 \(B_k\) 分别为雅可比矩阵，在特定工作点处计算得出。 随后利用后向差分法完成系统的离散化过程，从而便于数值求解。 --- #### 4. 预测方程与优化目标函数 给定未来 N 步的时间窗口，定义代价函数 J 如下： \[ J(U) = \sum_{i=0}^{N_p-1} (X_i - R)^T Q (X_i - R) + \sum_{j=0}^{N_c-1} (\Delta U_j)^T R_d (\Delta U_j), \] 这里： - \(Q\) 和 \(R_d\) 分别代表状态偏差权重矩阵以及控制变化量惩罚系数； - \(N_p\) 称作预测步长； - \(N_c\) 则指代控制更新周期数目。 最终目的是寻找使总成本最小的一组控制指令集合 {Δu₀,..., Δuₙ₋₁} ，并通过滚动时域策略不断重复此操作直至达到期望终点位置附近区域为止。 --- #### 5. 约束条件设置 实际工程实践中还需考虑物理层面的各种限制因素，比如最大允许加减速率、电机电流极限值等等。这些都可以作为附加不等式加入到原二次规划(QP)框架之中加以体现出来: \[ C_min ≤ C(X,U) ≤ C_max. \] --- #### 6. 数值求解器的选择 针对所形成的标准化QP子问题可以选择多种高效算法予以解答，例如Gurobi、OSQP或者是CasADi工具包内部集成的相关功能模块均能胜任此项任务需求。 --- ```python import numpy as np from scipy.optimize import minimize def mpc_control(x_current, u_prev, ref_traj, params): """ Model Predictive Control for differential drive robot. Args: x_current: Current state vector [x; y; theta]. u_prev: Previous control input [v; omega]. ref_traj: Reference trajectory points [[xr]; [yr]]. params: System parameters including L, dt etc. Returns: Optimal control inputs [v*, omega*]. """ def cost_function(u_flat): # Reshape flat array into matrix form u_pred = u_flat.reshape((-1, 2)) # Initialize variables total_cost = 0 x_pred = x_current.copy() for k in range(len(ref_traj)): # State prediction using kinematic model dx = u_pred[k][0]*np.cos(x_pred[2]) dy = u_pred[k][0]*np.sin(x_pred[2]) dtheta = u_pred[k][1] x_next = x_pred + np.array([dx, dy, dtheta]) * params['dt'] # Compute error and add to the cost function err_pos = ((ref_traj[k][:2]-x_next[:2])**2).sum() err_theta = abs((ref_traj[k][2]-x_next[2])) ctrl_effort = sum(abs(u_pred[k])) total_cost += err_pos + err_theta + ctrl_effort x_pred = x_next return total_cost res = minimize(cost_function, np.zeros(2*Np), method='SLSQP') return res.x[:2].reshape(-1) # Example usage of MPC controller with dummy data if __name__ == "__main__": initial_state = np.array([0., 0., 0.]) # Initial position & orientation prev_input = np.array([0.5, 0.]) # Last applied velocities reference_points = [(1., 1.), (-1., -1.)] # Desired waypoints system_params = {'L': 0.5, 'dt': 0.1} optimal_u = mpc_control(initial_state, prev_input, reference_points, system_params) print(f"Optimized Controls: Linear Velocity={optimal_u[0]}, Angular Velocity={optimal_u[1]}") ``` ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值