本文详细解析了如何利用MPU6050进行精准姿态采集,结合快速卡尔曼滤波算法和直流无刷电机的三环控制技术,从零构建一套高性能的自平衡控制系统。
一、平衡小车核心原理:倒立摆的稳定艺术
平衡小车的本质是一个移动的倒立摆系统。其核心控制目标是通过实时检测车身倾角(俯仰角 θ 和角速度 ω),计算出合适的电机控制量,驱动车轮产生加速度,抵消重力矩,使小车在竖直位置保持动态平衡。
核心物理模型:
I * α = m * g * h * sin(θ) - F * d
-
I:小车绕轮轴的转动惯量 -
α:角加速度 (dω/dt) -
m:小车质量 -
g:重力加速度 (9.8 m/s²) -
h:重心高度 -
θ:车身偏离垂直方向的角度 -
F:电机作用在轮子上的水平力 -
d:轮子半径
控制目标: 当 θ 增大时,电机需产生一个足够大的力 F,使角加速度 α 为负值(即减小 θ),将小车“拉”回平衡位置。
二、硬件系统架构与关键器件选型
平衡小车硬件系统由感知、决策、执行、供能四大模块构成。
1. 核心硬件模块功能表
| 模块 | 核心组件 | 关键功能 | 典型选型 |
|---|---|---|---|
| 感知模块 | 姿态传感器 (IMU) | 实时测量小车三维姿态角 (俯仰/横滚/偏航) 和角速度/加速度 | MPU6050 (集成陀螺仪+加速度计) |
| 电机位置/速度传感器 | 反馈电机转子位置、转速信息 (用于闭环控制) | 霍尔传感器 / 编码器 | |
| 决策模块 | 主控制器 (MCU) | 运行姿态解算、滤波算法、控制算法,生成电机驱动信号 | STM32F4xx (Cortex-M4, FPU) |
| 执行模块 | 直流无刷电机 (BLDC) | 将电信号转换为精确的转矩和转速输出 | Nidec 24V 3000RPM |
| 电机驱动器 | 将MCU的弱电控制信号转换为驱动电机的强电功率信号 | DRV8305 + MOSFET三相桥 | |
| 供能模块 | 电池 | 为整个系统提供能量 | 18650锂电池组 (7.4V/11.1V) |
| 电压转换模块 | 将电池电压转换为系统各部件所需的工作电压 (如5V, 3.3V) | DC-DC降压模块 |
2. MPU6050 传感器关键特性
| 参数 | 规格 | 说明 |
|---|---|---|
| 陀螺仪量程 | ±250, ±500, ±1000, ±2000°/s | 测量角速度范围,平衡车常用±500°/s |
| 加速度计量程 | ±2g, ±4g, ±8g, ±16g | 测量加速度范围,平衡车常用±4g |
| 通信接口 | I²C (标准模式 100kHz) | 与MCU通信的主要方式 |
| 数字输出接口 | 16-bit ADC | 提供高精度原始数据 |
| 集成功能 | DMP (可选) | 内置运动处理器,可分担部分姿态解算任务 |
| 工作电压 | 3.3V | 需电平匹配或LDO供电 |
三、软件系统架构与工程流程
采用分层、模块化的软件设计思想,确保系统实时性、可靠性和可维护性。
1. 软件架构层次图 (UML组件图)
+-----------------------+
| **应用层** |
| (平衡控制策略) |
+-----------------------+
|
v
+-----------------------+
| **算法层** |
| - 快速卡尔曼滤波 |
| - PID控制器(三环) |
| - 姿态解算(互补滤波) |
+-----------------------+
|
v
+-----------------------+
| **驱动层** |
| - MPU6050传感器驱动 |
| - BLDC电机驱动(FOC) |
| - 编码器/霍尔驱动 |
| - 定时器/PWM配置 |
| - ADC配置(电流采样) |
+-----------------------+
|
v
+-----------------------+
| **硬件抽象层** |
| (HAL库 / 寄存器操作) |
+-----------------------+
|
v
+-----------------------+
| **MCU硬件层** |
| (STM32F4xx 外设) |
+-----------------------+
2. 系统主程序流程图
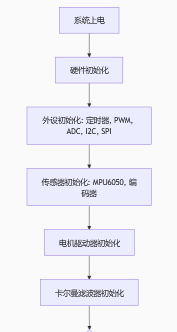
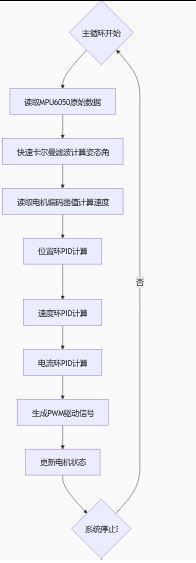
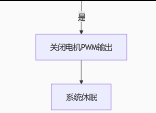
四、姿态解算核心:快速卡尔曼滤波算法详解
MPU6050提供的是噪声污染的原始数据,需融合陀螺仪动态特性和加速度计静态特性,通过卡尔曼滤波得到高精度姿态角。
1. 卡尔曼滤波五大核心方程

2. 应用于姿态估计的快速实现
针对嵌入式系统资源限制,采用一维简化模型(仅考虑俯仰角θ),大幅降低计算量:
-
状态变量:
x = [θ, gyro_bias]^T(角度 + 陀螺仪零偏) -
状态转移矩阵 A:
text
-
A = [[1, -Δt], [0, 1]] -
控制输入 B:
u = gyro_raw(原始角速度读数) -
观测矩阵 H:
H = [1, 0](仅观测角度) -
过程噪声协方差 Q: 建模系统动态不确定性
-
测量噪声协方差 R: 加速度计测量噪声方差
3. C语言实现代码片段
c
// 定义卡尔曼滤波器结构体
typedef struct {
float angle; // 最优估计角度 (rad)
float bias; // 陀螺仪零偏估计 (rad/s)
float P[2][2]; // 协方差矩阵
float Q_angle; // 过程噪声 - 角度
float Q_bias; // 过程噪声 - 零偏
float R_measure; // 测量噪声 (加速度计)
} KalmanFilter;
// 卡尔曼滤波更新函数
float kalmanUpdate(KalmanFilter *kf, float accel_angle, float gyro_rate, float dt) {
// 1. 预测步骤
kf->angle += dt * (gyro_rate - kf->bias);
kf->P[0][0] += dt * (dt * kf->P[1][1] - kf->P[0][1] - kf->P[1][0] + kf->Q_angle);
kf->P[0][1] -= dt * kf->P[1][1];
kf->P[1][0] -= dt * kf->P[1][1];
kf->P[1][1] += kf->Q_bias * dt;
// 2. 计算卡尔曼增益
float S = kf->P[0][0] + kf->R_measure;
float K[2] = {kf->P[0][0] / S, kf->P[1][0] / S}; // Kalman Gain
// 3. 更新状态估计
float y = accel_angle - kf->angle; // 测量残差
kf->angle += K[0] * y;
kf->bias += K[1] * y;
// 4. 更新协方差矩阵
float P00_temp = kf->P[0][0];
float P01_temp = kf->P[0][1];
kf->P[0][0] -= K[0] * P00_temp;
kf->P[0][1] -= K[0] * P01_temp;
kf->P[1][0] -= K[1] * P00_temp;
kf->P[1][1] -= K[1] * P01_temp;
return kf->angle; // 返回最优估计角度
}
五、直流无刷电机(BLDC)三环控制详解
为实现高精度、快速响应的电机控制,采用位置-速度-电流三闭环控制结构。
1. 三环控制系统结构图
plaintext
+-------------+ +-------------+ +-------------+ +-------------+
| 位置环PID | ---> | 速度环PID | ---> | 电流环PID | ---> | FOC |
| (外环) | | (中环) | | (内环) | | 算法 & PWM |
+-------------+ +-------------+ +-------------+ +-------------+
^ ^ ^ |
| | | |
+-----+-----+ +-----+-----+ +-----+-----+ +-----+-----+
| 编码器 | | 速度估计 | | 相电流 | | BLDC |
| 位置反馈 | | (M法/T法) | | 采样反馈 | | 电机 |
+-----------+ +-----------+ +-----------+ +-----------+
2. 各控制环功能与参数整定
| 控制环 | 输入量 | 输出量 | 核心功能 | 关键参数整定 |
|---|---|---|---|---|
| 电流环 | Iq_ref (期望电流) | Vq (q轴电压) | 控制电机转矩,响应最快 | KP_curr: 快速响应电流变化 KI_curr: 消除静差 |
| 速度环 | ω_ref (期望转速) | Iq_ref (q轴电流) | 稳定电机转速,抑制负载扰动 | KP_speed: 决定动态响应速度 KI_speed: 消除转速静差 |
| 位置环 | θ_ref (目标位置) | ω_ref (期望转速) | 精确控制电机转动角度 | KP_pos: 影响定位刚度 KD_pos: 抑制超调 |
3. 三环PID控制器C语言实现
c
// PID控制器结构体 (通用)
typedef struct {
float Kp, Ki, Kd; // PID参数
float integral; // 积分项
float prev_error; // 上一次误差 (用于微分)
float out_max; // 输出限幅
float out_min;
} PIDController;
// PID计算函数
float pidCompute(PIDController *pid, float setpoint, float measurement) {
float error = setpoint - measurement;
// 比例项
float P_out = pid->Kp * error;
// 积分项 (抗饱和)
pid->integral += error;
if (pid->integral > pid->out_max) pid->integral = pid->out_max;
else if (pid->integral < pid->out_min) pid->integral = pid->out_min;
float I_out = pid->Ki * pid->integral;
// 微分项 (防止设定值突变)
float derivative = error - pid->prev_error;
float D_out = pid->Kd * derivative;
pid->prev_error = error;
// 计算总输出并限幅
float output = P_out + I_out + D_out;
if (output > pid->out_max) output = pid->out_max;
if (output < pid->out_min) output = pid->out_min;
return output;
}
// 三环控制示例 (在定时中断中调用)
void motorControlLoop() {
// 1. 读取实际位置 (编码器计数)
int32_t actual_pos = readEncoder();
// 2. 位置环PID计算 -> 输出目标速度
float target_speed = pidCompute(&pid_pos, target_position, actual_pos);
// 3. 读取实际速度 (编码器差分/定时器计数)
float actual_speed = estimateSpeed();
// 4. 速度环PID计算 -> 输出目标q轴电流Iq_ref
float target_iq = pidCompute(&pid_speed, target_speed, actual_speed);
// 5. 读取实际相电流 (ADC采样 + Clarke/Park变换后得到Iq)
float actual_iq = getActualIq();
// 6. 电流环PID计算 -> 输出q轴电压Vq
float vq = pidCompute(&pid_current, target_iq, actual_iq);
// 7. 执行FOC算法 (SVPWM生成)
focSvpwm(vq, 0); // 假设Id_ref=0 (磁场定向控制)
}
六、系统调试与性能优化关键技巧
1. 姿态传感器标定流程
-
陀螺仪零偏标定: 静止放置 >10秒,计算各轴平均值作为零偏补偿值。
-
加速度计标定: 六面法旋转传感器,记录各面输出,计算标度因子和零偏。
-
安装误差补偿: 确保传感器坐标系与小车本体坐标系对齐。
2. PID参数整定口诀表
| 现象 | 问题环节 | 调整方向 | 物理意义 |
|---|---|---|---|
| 响应慢,收敛时间长 | 所有环 | ↑ Kp | 提高系统响应速度 |
| 静态误差大 | 速度/位置环 | ↑ Ki | 增强积分作用消除稳态误差 |
| 超调大,振荡剧烈 | 速度/位置环 | ↑ Kd | 增加阻尼抑制超调和振荡 |
| 高频抖动 | 电流环 | ↓ Kp, ↑ 滤波 | 减小高频增益,抑制噪声影响 |
| 启动时“冲”一下 | 位置环 | ↑ Kd 或 ↓ Kp | 抑制初始阶跃响应过冲 |
3. 关键性能指标对比
| 控制方案 | 稳态精度 | 动态响应 | 计算复杂度 | 抗干扰性 |
|---|---|---|---|---|
| 纯互补滤波 + 单环PID | 中 | 慢 | 低 | 弱 |
| 卡尔曼滤波 + 三环PID | 高 | 快 | 中 | 强 |
| 非线性控制 (如滑模) | 高 | 极快 | 高 | 极强 |
七、完整平衡控制策略实现
将姿态解算与电机控制结合,形成闭环平衡控制:
c
void balanceControlLoop() {
// 1. 读取MPU6050原始数据 (gyro, accel)
readMpu6050(&gyro, &accel);
// 2. 快速卡尔曼滤波计算车身俯仰角pitch
float pitch = kalmanUpdate(&kf, calculateAccelPitch(accel), gyro.y, dt);
// 3. 计算平衡控制量 (角度环PD控制)
float balance_output = Kp_balance * pitch + Kd_balance * gyro.y;
// 4. 叠加速度控制 (防止小车跑飞)
float speed_feedback = pidCompute(&pid_speed, 0, getWheelSpeed());
float motor_output = balance_output - speed_feedback;
// 5. 将控制量映射为左右电机目标转速
setMotorSpeed(MOTOR_LEFT, motor_output);
setMotorSpeed(MOTOR_RIGHT, motor_output);
}
八、工程挑战与解决方案
| 挑战 | 现象 | 解决方案 |
|---|---|---|
| 传感器噪声干扰 | 车身高频抖动 | 卡尔曼滤波优化Q/R参数,增加ADC采样滤波 |
| 电机响应滞后 | 平衡反应迟钝,易倒 | 提高电流环带宽,优化PWM频率,选用低电感电机 |
| 电池电压波动 | 不同电量下性能不一致 | 加入电压前馈补偿,或使用电流闭环而非电压开环 |
| 机械振动耦合 | 电机振动影响姿态读数 | 机械隔离IMU,软件低通滤波,提高传感器安装刚度 |
| 启动/停止冲击 | 上电瞬间猛转 | 软启动策略,缓增目标值;加入死区控制 |
附录:关键参数参考表
| 参数 | 符号 | 典型值范围 | 单位 | 说明 |
|---|---|---|---|---|
| 卡尔曼 Q_angle | Q_angle | 0.001 - 0.003 | - | 角度过程噪声 |
| 卡尔曼 Q_bias | Q_bias | 0.001 - 0.006 | - | 陀螺零偏过程噪声 |
| 卡尔曼 R | R_measure | 0.01 - 0.05 | - | 加速度计测量噪声 |
| 位置环 Kp | Kp_pos | 5.0 - 20.0 | - | 比例增益 |
| 速度环 Kp | Kp_speed | 0.05 - 0.2 | - | 比例增益 |
| 电流环 Kp | Kp_curr | 0.5 - 2.0 | A/V | 比例增益 |
| 平衡角度环 Kp | Kp_balance | 20.0 - 50.0 | - | 比例增益 |
| 平衡角度环 Kd | Kd_balance | 0.5 - 2.0 | - | 微分增益 |
| PWM 频率 | f_pwm | 16k - 20k | Hz | 电机驱动开关频率 |
| 控制周期 | T_control | 1 - 5 | ms | 算法执行间隔 |
通过本文详实的理论分析、代码实现和工程图表,读者可系统性掌握平衡小车核心技术。实际开发中需结合硬件平台特性反复调试,方能实现稳定、灵活的平衡效果。

























 2937
2937

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








