第一部分——状态估计机理（1）-- 概率论基础

一、概率密度函数

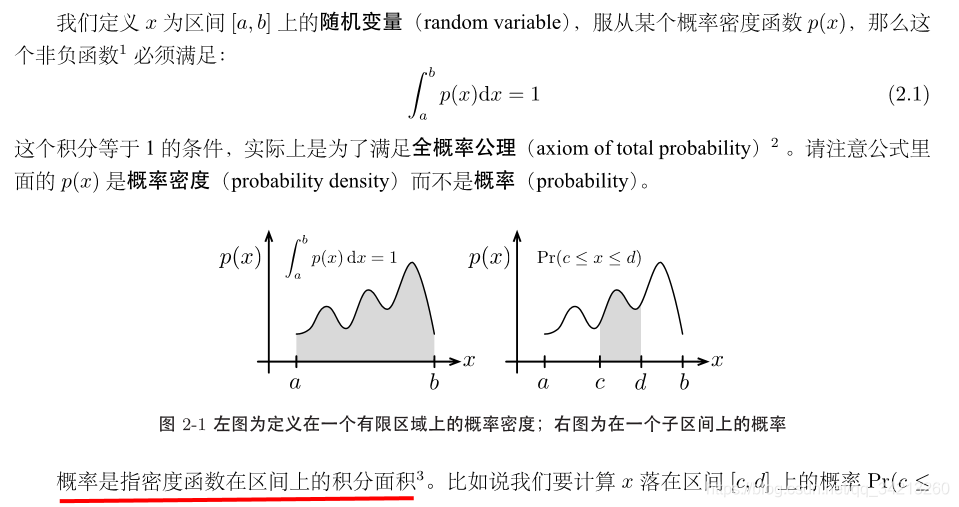
1.1 定义

1.2 贝叶斯公式及推断

x是待估计的机器人所处的状态，y是传感器的测量

• 先验概率是通过对以往经验分析对状态进⾏估计得到的概率；
• 后验概率指的在当前状态下，得到了⼀定的观测，或者造成了⼀定的效应，得到这个观测或者效应信息之后，对状态修正后的概率。

1.3 矩

1.4 样本均值和样本方差

更具体地说，这是因为N个样本的样本⽅差⾃由度是N−1，其中⼀个⾃由度因为均值⽽消去，所以归⼀化系数是1/(N−1)

1.5 统计独立性与不相关性

1.6 归一化积

1.7 负熵和互信息

1.8 克拉美罗下界和费歇尔信息量

我们⽤^来表⽰估计（estimated）量。

二、高斯概率密度函数

2.1 定义

2.2 Isserlis定理

2.3 联合高斯概率密度函数，分解与推断

2.4 统计独立性，不相关性

我们也可以从另⼀个⾓度来思考这件事。⾸先假设变量是不相关的，那么Σ
xy=0，于是它们是统计独⽴的。既然这些条件都是⼀样的，在⾼斯概率密度函数的情况下，就可以相互替代着使⽤统计独立和不相关的术语。

2.5 高斯分布随机变量的线性变换

2.6 高斯概率密度函数的归一化积

2.7 Sherman-Morrison-Woodbury等式

对于可逆矩阵，我们可以将它分解为⼀个下三⾓—对⾓—上三⾓（lower-diagonal-upper，LDU）形式或上三⾓—对⾓—下三⾓（upper-diagonal-lower，UDL）形式，如下所⽰:

2.8 高斯分布随机变量的非线性变换

闭式解就是解析解

2.9 高斯分布的香农信息

2.10 联合高斯概率密度函数的互信息

2.11 高斯概率密度函数的克拉美罗下界

三、高斯过程