本小节文字比较少,但是理解起来内容还是蛮难的,花了我整整一天的时间把代码和前面的原理搞明白,其实最难的部分就在本小节的代码上。
最小二乘法求得最优解为t,可以求得泛化函数为f(t)。上市过程是回归的过程,分类与回归的区别就在于回归给出的是自变量对应的预测解,而分类问题需要给出的是结果的类别。所以在这里加上一个函数sign,定义为下:
当f(t)<0 sign(f(t))=-1; 当f(t)=0 sign(f(t))=0; f(t)>0 sign(f(t))=1;
例子是高斯核函数,使用最小二乘法进行模式识别,与线性判别分析算法是一致的,在线性判别分析中,当正负两类样本都服从协方差矩阵相同的高斯函数时取的最佳结果。
针对线性判别分析算法https://www.cnblogs.com/pinard/p/6244265.html刘老师讲的已经很详细了,在这里提出一点个人的想法,在证明如下的公式的时候可以使用,当然
表示的是特征值,这样数提到前面,可以知道这个式子能够得到所有的特征值,而且上界和下界分别是最大特征值和最小特征值。
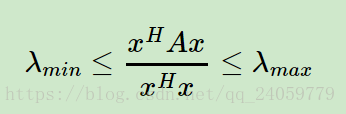
依照上面的等价替换,下面的式子都很好得以证明:
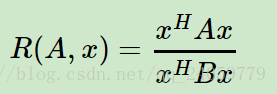
上面的式子的范围就是A取最大特征值,B取最小特征值的时候。下面的证明同理。
下一个概念就是协方差矩阵:
谈到协方差矩阵肯定要先从方差矩阵开始,因为协方差只不过不是针对单个对象而是互相之间协调的方差
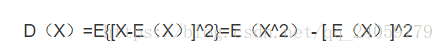
方差就是每一个变量对期望(可以暂时理解为平均值)之间的差值,但是差值有正有负,很容易抵消,所以取平方使所有差值都为正数,这样就得到总体样本对平均期望之间的一个偏离程度。
协方差就是多个变量总体对多个样本期望的偏离程度:
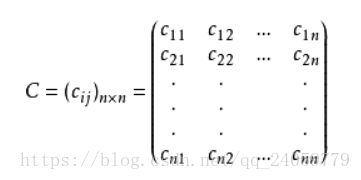
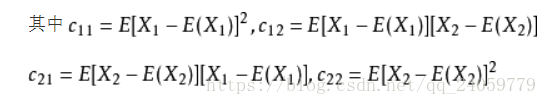
每一个变量针对他自己期望的偏离程度对所有偏离程度取乘积,真正计算的时候可以用这个公式:
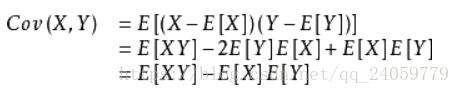
下面简单介绍一个等高线的概念,本人自己理解,在地理图形中,针对某一个水平面作为基准面,高度相同的所有点连接起来投影到水平面上就是等高线,在矩阵中,空间矩阵中所有针对二维平面高度相等的向量连接成曲线投射到能够表现的二维平面上就是多维矩阵的等高线。
话不多说了,开始解释和证明代码:

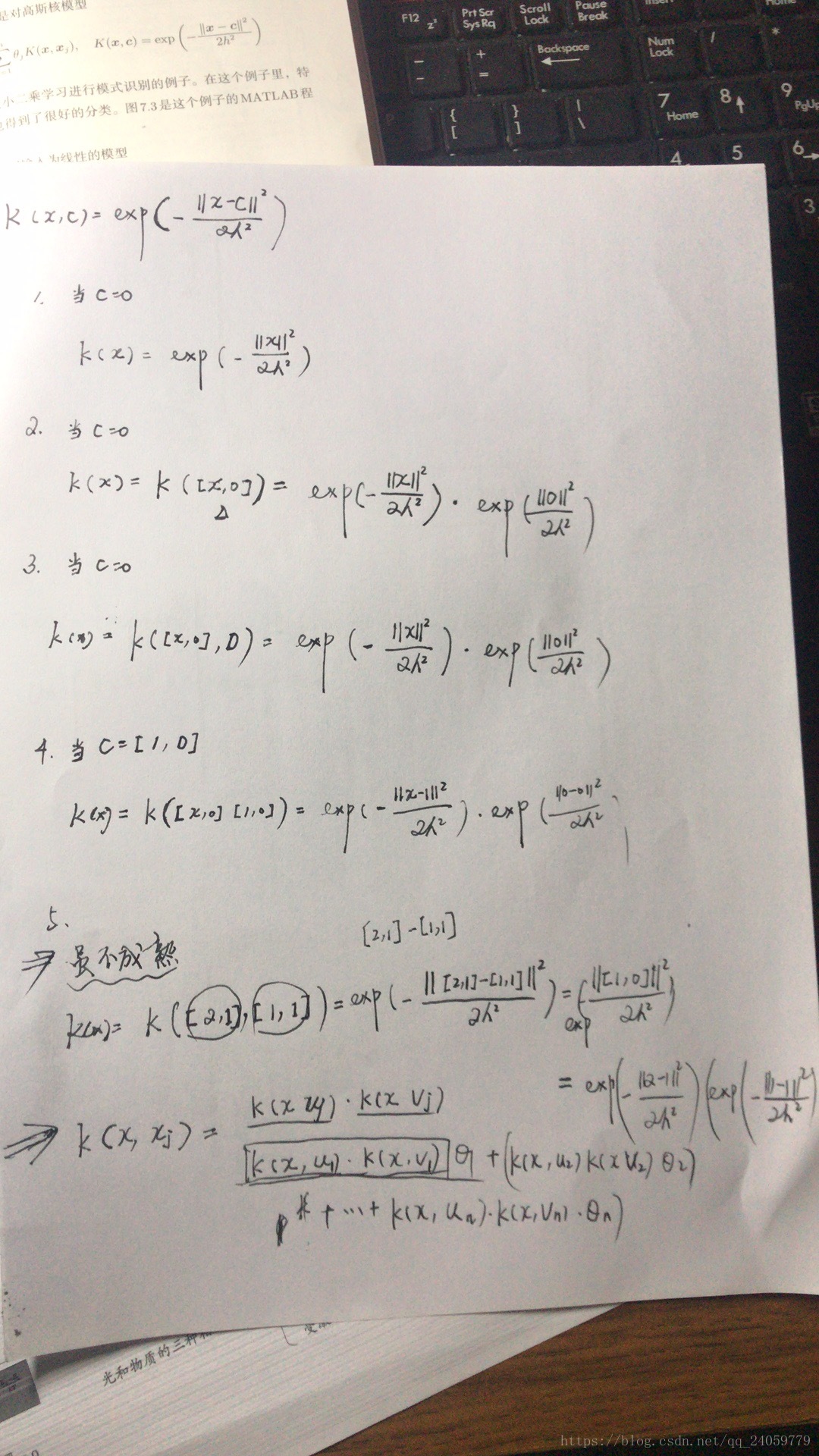







 本文深入探讨了最小二乘法求解最优参数的方法,及其在模式识别中的应用,特别是高斯核函数下的线性判别分析。文章通过实例解析了回归与分类的区别,并详细解释了代码实现。
本文深入探讨了最小二乘法求解最优参数的方法,及其在模式识别中的应用,特别是高斯核函数下的线性判别分析。文章通过实例解析了回归与分类的区别,并详细解释了代码实现。
















 4195
4195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








