图解机器学习-0/1分割和间隔-多分类的基本技巧

最新推荐文章于 2024-03-26 13:38:39 发布

原创最新推荐文章于 2024-03-26 13:38:39 发布 · 1.6k 阅读

0 ·

CC 4.0 BY-SA版权

matlab 同时被 2 个专栏收录

31 篇文章

订阅专栏

图解机器学习

26 篇文章

订阅专栏

本文探讨了在机器学习中，如何通过增大分类间隔来减少分类错误，解释了0/1损失函数的概念，并介绍了用于多类别分类的两种方法。同时，文章深入分析了间隔与损失函数之间的关系，以及如何选择最优的分类间隔。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先是间隔这个概念,参考吴孟达老师笔记的这篇博客:

https://blog.youkuaiyun.com/blackyuanc/article/details/78904729

其实简单点来理解,间隔就是样本点与分割线之间的距离,当间隔大的时候,样本点与分类线之间的距离远,分类效果明显.当样本点的间隔小,即与分类线之间的距离很小,这样当学习继续进行,很有可能该分类点从一个分类区间分到了另一个分类区间,使得分类算法的分类错误增加,所以尽量保持一个比较大的分类间隔,使得所有样本点都尽可能的离分类线尽量的远,使得分类错误少,损失小.

0/1最小化损失函数:

$\underset{\theta }{min}\frac{1}{2}\sum_{i=1}^{n}(1-sign(f_{\theta }(x_{i})y_{i}))$

损失:

即每次分类错误都会累加1,损失也可以理解为错误个数.损失函数值越大说明错误分类越多,所以为了使分类的效果最好就是使得损失函数的值最小的过程.上述函数感觉不用具体分析了,就是当分类结果与实际结果符号相同表示分类正确,损失值为0,当预测分类与实际分类符号相反,则分类错误,分类结果值为-1.

上述函数的求解过程可以归并为离散最优化问题,这个词汇看起来很吊,以后在研究,这个方程告诉了上述方程的解空间是一个2^n的指数爆炸,所以简单的操作是不能够求解最优解的,因此使用代理损失函数来替换原函数,0/1分割的代理损失函数是l2损失,

另间隔 $m=f_{\theta }(x)y$ ,则L2学习的残差就可以表示为: $r^{^{2}}=(1-m)^{2}$

可以知道当m<1的时候,损失有可能趋向于无穷大,当m>1的时候,损失也可能趋向于无穷大,所以m=1的时候可以得到不错的分类结果,但是不是最优的分类结果,因为最优的分类结果的损失函数和间隔应该满足如下两条规则:

1间隔m的函数是单调递减的,

2间隔m=0的时候微分为负数,即当间隔为负数(即分类错误)的时候能够向着m为正数(即分类正确)的方向走.即当m=很大的值的时候,分类的损失将变得很小很小,因为错误的分类样本都变得正确了.

满足以上两条规则的m间隔函数可以得到损失函数的最优解,

针对多类别的情形有两种方法都是根据两类分类思想提出来的:

第一种方法是有c个类别的样本情况下,把其中一个类别定义为1,其余所有的类别都定义为-1,在这样的情况下对c个类别中的每一个类别做一次上述的二分损失函数,当测试样本来的时候代入上述的每一个损失函数,当样本确实在这个类别的时候损失函数的函数值会是最小的,当样本不在这个类别的时候损失函数的函数值会很大,这样针对损失函数的函数值最小的类别,就是这个样本的类别.

第二种方法是在c类样本的情况下,把其中每两队当做二分类,其中一个为1,一个为-1,需要注意的是顺序前面的小后面的大,然后根据二分类的sign公式,看看训练样本在那个类别中,当sign=1的时候给第一个样本加一票,当等于sign=-1的时候给第二类样本加一票,以此累加,一直到最后哪一个类别得到得票数最多,则训练样本就属于这个类别

以上两种方法都是通过最简单的二分类的基本思想推导出来的.

>> rand('state',0);randn('state',0);
>> n=200;a=linspace(0,4*pi,n/2);
>> u=[a.*cos(a) (a+pi).*cos(a)]'+rand(n,1);
>> v=[a.*sin(a) (a+pi).*sin(a)]'+rand(n,1);
>> x=[u v]; y=[ones(1,n/2) -ones(1,n/2)]';
>> x2=sum(x.^2,2);hh=2*1^2;l=0.01;
>> k=exp(-(repmat(x2,1,n)+repmat(x2',n,1)-2*x*x')/hh);
>> t=(k^2+l*eye(n))\(k*y);
>> m=100;X=linspace(-15,15,m)';X2=X.^2;
>> U=exp(-(repmat(u.^2,1,m)+repmat(X2',n,1)-2*u*X')/hh);
>> V=exp(-(repmat(v.^2,1,m)+repmat(X2',n,1)-2*v*X')/hh);
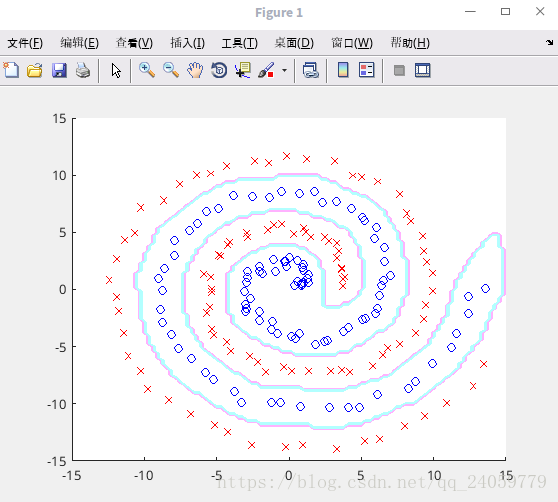
>> figure(1);clf;hold on;axis([-15 15 -15 15]);
警告: MATLAB 已通过改用 OpenGL 软件禁用了某些高级的图形渲染功能。欲了解有关详细信息，请点击此处。 
>> contour(X,X,sign(V'(U.*repmat(t,11,m))));
 contour(X,X,sign(V'(U.*repmat(t,11,m))));
                    ↑
错误: 圆括号或方括号不对称或异常。
 
>> contour(X,X,sign(V'*(U.*repmat(t,1,m))));
>> plot(x(y==1,1),x(y==1,2),'bo');
>> plot(x(y==-1,1)),x(y==-1,2),'rx');
 plot(x(y==-1,1)),x(y==-1,2),'rx');
                                 ↑
错误: 圆括号或方括号不对称或异常。
 
>> plot(x(y==-1,1),x(y==-1,2),'rx');
>> colormap([1 0.7 1;0.7 1 1]);
>>