
>> rand('state',0);randn('state',0);
n=50;N=1000;x=linspace(-3,3,n)';X=linspace(-3,3,N)';
pix=pi*x;y=sin(pix)./(pix)+0.1*x+0.2*randn(n,1);
y(n/2)=-0.5;
hh=2*0.3^2;l=0.1;e=0.1;
x2=x.^2; X2=X.^2;
t0=randn(n,1);
%l2最小二乘学习
k=exp(-(repmat(x2,1,n)+repmat(x2',n,1)-2*x*x')/hh);
K=exp(-(repmat(X2,1,n)+repmat(x2',N,1)-2*X*x')/hh);
t1=k\y;F1=K*t1;t2=(k^2+l*eye(n))\(k*y);F2=K*t2;
figure(1);clf;hold on;axis([-3 3 -1 1.5]);
plot(x,y,'bo');
plot(X,F1,'g-');
plot(X,F2,'K-');
%l1约束的l2最小二乘学习
for o=1:1000
t=(k^2+l*pinv(diag(abs(t0))))\(k*y);
if norm(t-t0)<0.001,break,end
t0=t;
end
F3=K*t;
plot(X,F3,'r-');
%huber
for o=1:1000
r=abs(k*t0-y);w=ones(n,1);w(r>e)=e./r(r>e);
Z=k*(repmat(w,1,n).*k)+l*pinv(diag(abs(t0)));
t=(Z+0.000001*eye(n))\(k*(w.*y));
if norm(t-t0)<0.001,break,end
t0=t;
end
F4=K*t;
plot(X,F4,'m-');
>>
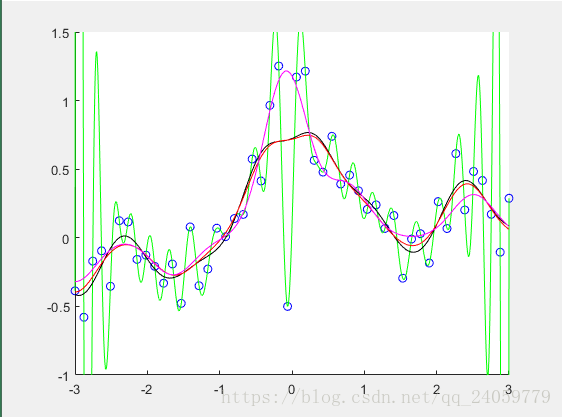
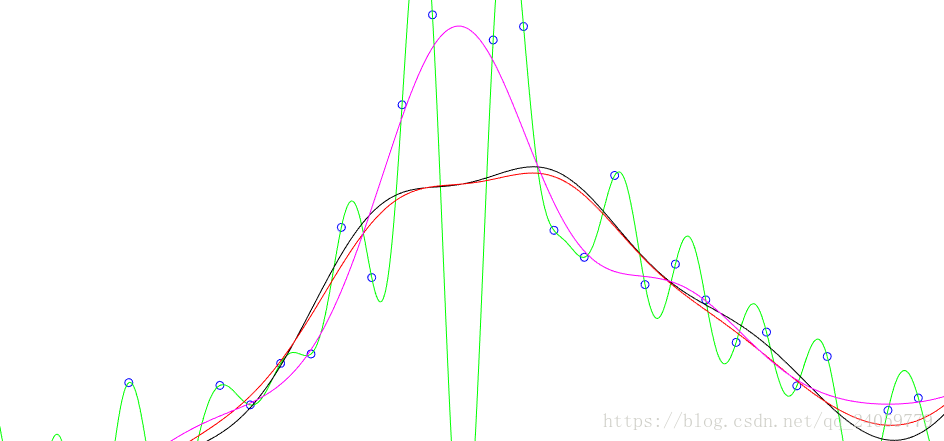







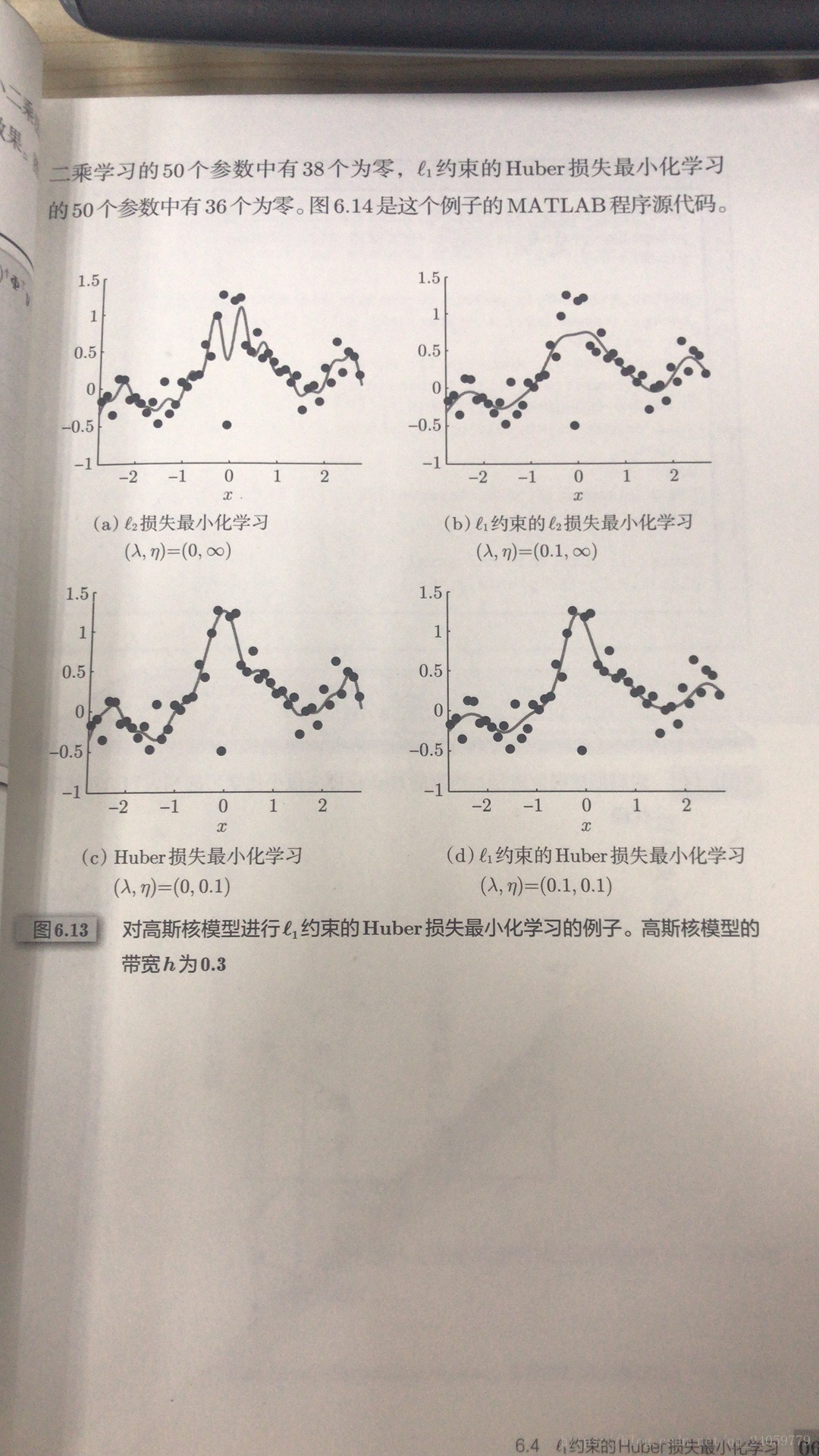
 本文通过Matlab代码展示了不同类型的最小二乘学习方法,包括标准最小二乘、带有l1约束的最小二乘及Huber损失下的最小二乘,并对结果进行了可视化比较。
本文通过Matlab代码展示了不同类型的最小二乘学习方法,包括标准最小二乘、带有l1约束的最小二乘及Huber损失下的最小二乘,并对结果进行了可视化比较。
















 1066
1066

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








