图解机器学习-图基损失最小化学习-matlab

>> rand('state',0);randn('state',0);
n=10;N=1000;x=linspace(-3,3,n)';X=linspace(-4,4,N)';
y=x+0.2*randn(n,1);y(4)=-4;y(5)=3;
p(:,1)=ones(n,1);p(:,2)=x;t0=p\y;t1=p\y;e=1;
for o=1:1000
r=abs(p*t0-y); w(:,1)=ones(n,1);w(r>e)=e./r(r>e);
t=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t-t0)<0.001,break,end
t0=t;
end
>> for o=1:1000
r=abs(p*t0-y); g(:,1)=zeros(n,1);g(r<=e)=(1-r(r<=e).^2/e^2).^2;
t3=(p'*(repmat(g,1,2).*p))\(p'*(g.*y));
if norm(t3-t1)<0.001,break,end
t1=t3;
end
>>  P(:,1)=ones(N,1); P(:,2)=X;
>> F=P*t;
>> K=P*t1;
>>  figure(1);clf;hold on;axis([-4 4 -4.5 3.5]);
plot(x,y,'bo');
>> plot(X,F,'g-');
>> plot(X,K,'k-');
>> 

 

 

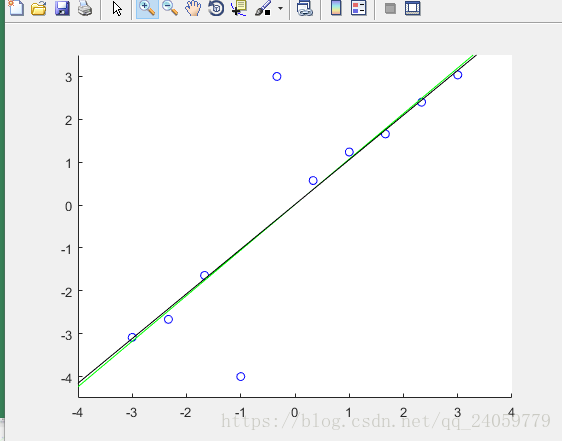
由图像可以很容易看出使用Tukey方法确实能够使得回归问题受到的干扰更小。