多变量名义数据的语义噪声保护

多变量名义数据集的扰动数据保护

梅赛德斯·罗德里格斯‐加西亚1,大卫·桑切斯1(&)，以及
蒙特塞拉特·巴特2
1联合国教科文组织数据隐私讲席，计算机工程与数学系，塔拉戈纳 大学罗维拉‐维尔吉利，西班牙塔拉戈纳 mercedes.rodriguez@uca.es,david.sanchez@urv.cat
2互联网 跨学科研究所（IN3），加泰罗尼亚开放大学，西班牙卡斯特尔德费 尔斯montserrat.batet@urv.cat

1 引言

个人数据在商业和研究方面都至关重要。微观数据（多变量记录，每条记录详 细描述一个个体的属性）尤其受到关注，因为与宏观数据不同，它们不限制数 据分析的类型和粒度。然而，发布微观数据用于二次利用可能会损害个体的隐 私。为了在保护隐私的同时确保数据具有分析价值，数据保护方法[1, 2]旨在 平衡披露风险与数据效用保持之间的权衡。

尽管大多数保护方法都集中在数值数据上，但如今，名义微观数据（分类 值或文本响应）在来自社交网络、民意调查、医疗记录或网页浏览的个人数据 中占据了相当大的比例[3]。与数字不同，名义数据是有限的、离散的，且通常 是非有序的。因此，无法应用数据掩蔽所需的算术和统计操作符。此外，数值 数据的效用取决于其统计特性，而名义数据的效用则依赖于语义的保留[4]。本 文应对这一具有挑战性的场景，并特别关注多变量名义数据集，这类数据集对 研究尤为重要。

1.1 相关工作

在统计披露控制[1]和隐私保护数据发布[2]领域中，已提出了许多数据保护方 法。对于名义数据，基于用泛化替代原始值的非扰动方法是最为广泛使用的方 法。然而，这些方法存在若干缺陷，可能损害数据效用[5]。首先，泛化会导致 粒度损失，因为输入值被替换为数量较少的类别/泛化值。此外，如果样本中存 在离群值，则对其泛化的需要可能导致非常粗略的泛化，从而造成信息/效用的 大量丢失。

扰动方法（如数据微聚集、秩交换、数据混洗或噪声添加）不受这些缺点 的影响，因为它们在保持数据粒度的同时对数据进行掩蔽。其中，只有微聚集 已被调整用于语义上掩蔽名义数据[6, 7]。微聚集通常通过构建包含k个不可 区分记录的簇，并将原始值替换为簇的代表值（例如均值），以实现k‐匿名性 [8]。为了最小化替换带来的信息损失，微聚集要求使用静态同质数据。

相比之下，噪声添加能够对记录进行个体级掩蔽，这在数据以流形式生成 且需要实时保护时非常有用[9]。此外，与基于同质数据聚合的方法不同，噪声 添加允许定义个体级扰动/掩蔽级别，从而满足异构隐私需求。最后，由于e‐差 分隐私模型的实施依赖于拉普拉斯噪声添加，噪声添加最近变得更加重要[10], 。

由于其数学根源，噪声添加很少应用于分类/名义数据。在[11]中，作者 提出根据概率分布更改每个属性的值。在[12],中，建议将分类属性划分为呈现 自然顺序的子属性，这是噪声添加所必需的。在差分隐私的背景下，已提出一 些机制来扰动离散数据：几何机制（一种离散概率分布，可作为拉普拉斯机制 的替代）[13]和指数机制（以概率方式选择离散函数的输出）[14]。然而，这 两种机制都依赖于数据分布而非语义；这一事实使它们更适用于离散数值而非 名义数据。在[15]中，建议使用“语义噪声”来掩盖文本，但未具体说明其计 算方法。

1.2 贡献

在[16]中，我们提出了语义噪声的概念，作为数值不相关噪声添加的基于语义 的版本。通过该方法，我们能够掩盖个体名义属性，同时比仅基于数据分布的 扰动机制更好地保持其语义。

在本文中，我们将这项工作扩展到支持相关噪声，这是为了在保护多变量数据集中 非独立属性的同时保留其相关性。与[16],类似，我们利用本体来捕获和管理名义值的底层语义，并采用 语义操作符替代用于数值噪声添加的算术操作符（即距离、均值、方差和协方 差）。最后，我们提出一种语义算法，用于向成对的名义属性添加用户定义的 相关噪声。

本文其余部分组织如下。第2节介绍（数值）噪声添加的背景。第3节描 述名义值的语义管理，并详细介绍我们的语义相关噪声添加方法。第4节报告 针对名义多变量数据集进行的若干实证实验的结果。第5节阐述结论并提出一些 未来研究方向。

2 背景

不相关噪声[17]通过对每个属性添加正态分布的随机噪声来扰动各个属性。假 设有一个数据集X，其构成一个(n p)矩阵，包含n条记录的p个属性，其中
Xj={x1j,…,xij,…,xnj}表示第j个属性，而xij表示对应于个体/记录i的属性j的
值。为了扰动属性Xj，每个值xij被替换为一个带噪声的版本zij：

Zj ¼ Xj þ ej; ð1Þ

其中ej={1j,…,ij,…,nj}是噪声序列。设Xj*N(lXj,rX2j)为均值为lXj 、方差
为rX2j的向量，ej*N(0,rX2j)是服从正态分布的随机误差向量，其均值为零，方 差为rX2j。误差方差rX2j 与原始属性方差成比例，如下所示：

r2 e j
¼ ar2 X j
; a[0 ð2Þ

因子a决定了噪声量，其值通常在0.1到0.5[18]之间。该方法保持属性的均 值，并使方差在 1+ a的因子下成比例；但由于噪声是独立地应用于每个属性， 添加噪声属性之间的协方差为零，因此属性相关性未被保留。

为了解决这一问题，鉴于大多数数据集都是多变量且具有相关性的，并且 许多数据分析是针对记录而非属性进行的，因此提出了相关噪声添加方法[19]。

应用于数据集X多个属性的噪声遵循矩阵表示法：

Z ¼ X þ e; ð3Þ

其中，(n p)数据矩阵X*N(lX,RX)服从均值为p维向量lX、协方差矩阵为(p p)矩阵RX的多变量正态分布。RX的对角元素是属性的方差，非对角元素

元素是属性之间的协方差。类似地，e*N(0,Re)是一个(n p)矩阵，包含 p个噪声序列，每个序列有n个误差值。噪声矩阵e也服从多元正态分布，其 均值为p维零向量，协方差矩阵为(p p)矩阵Re。误差的协方差矩阵与数据 的协方差成比例：

Xe ¼ aXX; a[0 ð4Þ

添加相关噪声可保持每个属性的均值，使协方差矩阵与原始数据的协方差 矩阵成比例（比例因子为 1+ a），并维持属性之间的相关性。

3 使用语义相关噪声的名义数据扰动

我们提出了一种（扰动式）相关噪声添加方法，用于掩盖多变量名义数据集， 该方法利用本体来捕捉和管理数据语义。其思想是用其他语义上相似的概念替 换原始值，其相似性与期望的噪声幅度成比例（该幅度表明了应用于数据的掩 蔽程度）。

3.1 名义数据的语义管理

为了管理名义数据的语义，我们首先根据本体中建模的概念来定义属性的语义 域，我们将本体作为知识库加以利用。一个本体可以被视为一个树/图，其节点 表示某个知识领域的概念，边则描述它们之间的语义关系。因此，我们的方法 假设目标领域存在适当的本体可供使用。

设A={a1,…,ai,…,an}为包含n条记录的数据集X的一个属性，其中ai是
个体i的值，映射到s中的一个概念。属性A的语义域定义为属于A类别的概念集 合（例如，如果A包含疾病，则D(A)是所有疾病的集合）。

DðAÞ ¼ c 2 CategoryðAÞ f g ð5Þ

然后，我们从本体中提取语义域D(A)的分类体系，作为层次结构 s(D(A))，该结构包含所有属于D(A)的最小公共上位概念LCS(D(A))的分类特 化概念；即s中包含D(A)中所有概念的最具体的祖先。

sðDðAÞÞ ¼[
c i 2s ci j LCSðDðAÞÞ ci f g ð6Þ

与数值域不同，D(A)是有限的、离散的，且通常是非有序的。为了处理D(A)，在 [16]中我们定义了用于不相关噪声添加所需的算术操作符的语义版本（即距离、均值和 方差）。由于这些操作符也用于相关噪声添加，因此我们在此简要介绍它们。

最基本的算子是用于度量两个值之间距离的算子。在语义域中，名义值应 根据其所指概念的语义进行比较，两个概念ci和cj在含义上的相异性可通过它 们的语义距离sd(ci,cj)来计算。本文选用著名的吴和帕尔默（W&P）语义相似
性度量的距离形式[20]来计算sd(ci,cj)，因为它提供的值被归一化到范围[..
1],内，这与正态噪声分布一致；它对距离的评估既非对数也非指数形式，避免 了输出范围高低区域的值过于集中，并且具有较高的计算效率。

通过依赖语义距离sd(,)，我们可以将标称属性A的语义均值定义为来自 s(D(A))的概念c，该概念使相对于A中所有ai的语义距离之和最小。

slðAÞ ¼ arg min c2sðDðAÞÞ X ai2A sd c; ai ð Þ
!
ð7Þ

另一方面，标称属性A的语义方差可以定义为A中每个概念ai与语义均值 sl(A)之间的语义距离平方的平均值。

sr2ðAÞ ¼ P a i2 A
sd ai; slðAÞ Þ ð Þ2
n
ð8Þ

如第2节所述，对于相关噪声添加，我们还需要两个额外的操作符来度量属 性对之间的线性依赖关系：协方差和相关性。在数值域中，当一个属性的较大 值主要对应另一个属性的较大值，且较小值也相应对应时，标准算术协方差为 正。为了区分大值和小值，属性域上必须存在全序关系，数值即为此类情况。

然而，名义属性的域通常是非有序的，因此我们需要一种不依赖于全序关系的 统计依赖性度量方法。

在[21],塞凯伊定义了距离协方差和距离相关性；它们通过依赖每变量取值 之间的成对距离（或相异性）来度量变量间的统计依赖性。在本文中，我们通 过依赖上述语义距离sd(,)，将这些度量方法应用于名义数据领域。

设A={a1,…,an}和B={b1,…,bn}为n个个体样本中的两个名义属性，其中ai和
bi表示第i个个体的取值。根据距离协方差的定义，我们必须首先计算n×n的距离矩阵

每个属性。为此，我们必须计算每个属性的所有成对距离，这些距离在语义域 中对应于名义值对之间的语义距离sd。距离矩阵用于获得n乘n双中心距离矩 阵，对于属性A，其计算方式如下：

dAij n
i;j¼1¼ sdðai; ajÞ dAi: dA:j þ dA::
n
i;j¼1;
ð9Þ

其中，sd(ai,aj)表示属性A的距离矩阵中第(i,j)th 个元素的值，dA i:表示距离矩 阵第ith 行的均值，dA:j 表示距离矩阵第jth 列的均值，dA:: 表示距离矩阵所 有值的均值（即总平均值）。对于属性B，符号表示类似。

然后，两个名义属性A和B之间的语义距离协方差是乘积dA ijd B ij的算术平 均数的平方根。它满足sdCov(A,B) 0，且当且仅当A和B独立时为0[21]。

sdCov A; B ð Þ¼ 1
n
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi X n
i;j¼1
dAij d B ij tvuu ð10Þ

关于数值相关性，两个名义属性A和B的语义距离相关性可以通过将其距离 协方差sdCov(A,B)除以它们的距离标准差的乘积得到的非负数来计算。

sdCorðA; BÞ ¼
sdCovðA;BÞ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi sdVarðAÞ sdVarðBÞ p
; sdVarðAÞ sdVarðBÞ[0
0; sdVarðAÞ sdVarðBÞ ¼ 0 ( ; ð11Þ

其中，sdVar(A)和sdVar(B)是属性A和B的语义距离方差，它们是距离协方差 的一种特殊情况，即当两个属性相同时（例如，sdVar(A)= sdCov(A,A)）。

语义距离相关性的结果被限定在[..1]范围内，且当且仅当A和B独立时为0。

与数值情况类似，接近零的值表明属性之间的语义关联较弱，而较大的值则表 明存在更强的关联。

多变量名义数据集的扰动数据保护

3.2 多变量数据集的语义噪声

在本节中，我们将标准的相关噪声添加方法应用于名义数据的语义域。我们方法的目标有两个：（i）通过使用与期望的保护级别相一致的语义距离内的术语来替换原始名义值，从而掩盖原始名义值；（ii）尽可能保留数据的语义特征。
关于后者，我们的具体目标是尽可能保留每个属性的语义均值；获得与原始数据方差和噪声幅度成比例的每属性离散度；获得一个成对属性离散度与原始数据的协方差和噪声幅度成比例；并尽可能保持属性之间的语义相关性。

与不相关噪声不同，相关噪声序列必须考虑属性之间的相关程度，以保持它们的关联水平（见第2节）。为简化以下说明，假设数据集X仅包含两个名义属性A和B，且有n条记录（对于包含多于两个属性的数据集，下述过程将应用于属性对）。基于上述详细的操作符，生成的语义相关噪声是一个(n 2)维随机数矩阵eA,B={(a1, b1),…,(ai, bi),…,(an,bn)}，该矩阵服从多元正态分布eA,B *N(0,aRA,B)，其均值为零向量，协方差矩阵为aRA,B，其中a为期望的语义噪声水平。

XA;B ¼ sdVarðAÞ sdCovðA; BÞ sdCovðB;AÞ sdVarðBÞ
ð12Þ

在数值域中，噪声幅度可以直接且一致地加/减到原始值上。具体而言，如果向一个大于（小于）属性样本中任何其他值的原始值添加正噪声，则掩码值将以相同幅度远离（更接近）样本中的其他值；相反，如果噪声为负，则掩码值将更接近（远离）样本中的其他值。由于误差围绕零呈正态分布，总的加/减幅度相互补偿，从而使掩码结果中的聚合的相对差异得以保持，进而保留数据的统计特征，例如均值。

在语义域中，我们建议将原始名义值替换为底层分类法s(D())中的其他概念，其语义距离理想情况下等于噪声幅度。然而，由于名义数据不是有序的，如果我们用某一特定距离的另一个概念替换原始值，则无法保证该新概念与其他值之间的距离也更接近或更远。

为了解决这一问题，我们提出了一种启发式方法，该方法根据噪声符号指导值替换，旨在改善属性间相关性的保留。通常情况下，为了更好地保留两个属性A和B之间的相关性，如果向一个大于（小于）其对应值bi的原始值ai添加了正噪声，则新值应以相同的幅度远离（接近）bi；相反，如果误差为负，则新值应更接近（远离）bi。这样，对之间累积的加法和减法的幅度将相互抵消。

为了平衡属性值对之间的“移动”次数并保持属性相关性，我们提出的启发式方法将噪声符号相对于被替换值所对应的配对定义的参考点进行解释：如果噪声是正的，则s(D(A))中将替换ai的概念c必须比ai离其配对bi更远，即 sd(c,bi)>sd(ai,bi)，反之亦然；如果噪声是负的，则概念c必须比ai更接近bi，即sd(c,bi)< sd(ai,bi)，反之亦然。显然，两个属性必须属于同一语义域，即 s(D(A))= s(D(B))。

算法1根据所提出的启发式方法形式化了语义相关噪声添加过程。首先，获取与属性A和B的域相关联的分类法s(D(A))和s(D(B))，具体方法详见第3.1节。
然后，将每个属性的值映射到s(D(A))和s(D(B))中的概念。在第4和第5行，构建(2 2)协方差矩阵RA,B，并生成(n 2)噪声矩阵eA,B*N(0,aRA,B)。最后，在第6到第14行，根据期望的相关噪声幅度并遵循所提出的启发式方法对属性 A进行掩码处理。对属性B也应用相同的过程。

需要注意的是，为了提供先验隐私保证，我们的方法应应用于基于噪声的隐私模型中，例如e‐差分隐私[10]。通过专门设计的噪声分布，该模型可保证输出对单个输入记录的修改不敏感（最多取决于e的一个因子）。这样，个体参与调查（或其在调查中贡献的任何具体信息）不会因超过 1+ e因子而受到威胁。

4 实验

在本节中，我们使用两个属性相关性程度显著不同的名义数据集来评估第3节提出的算法，并将其与我们在[16]中提出的语义不相关噪声添加方法进行比较。
作为评估数据，我们使用了加利福尼亚州全州卫生规划与发展办公室提供的患者出院数据集，其中每条记录描述了一名患者并包含两个相关的名义属性：主要诊断和次要诊断。SNOMED‐CT[22],，一个对数据集中所有诊断进行建模的医疗知识库，已被用作提供数据语义的本体。

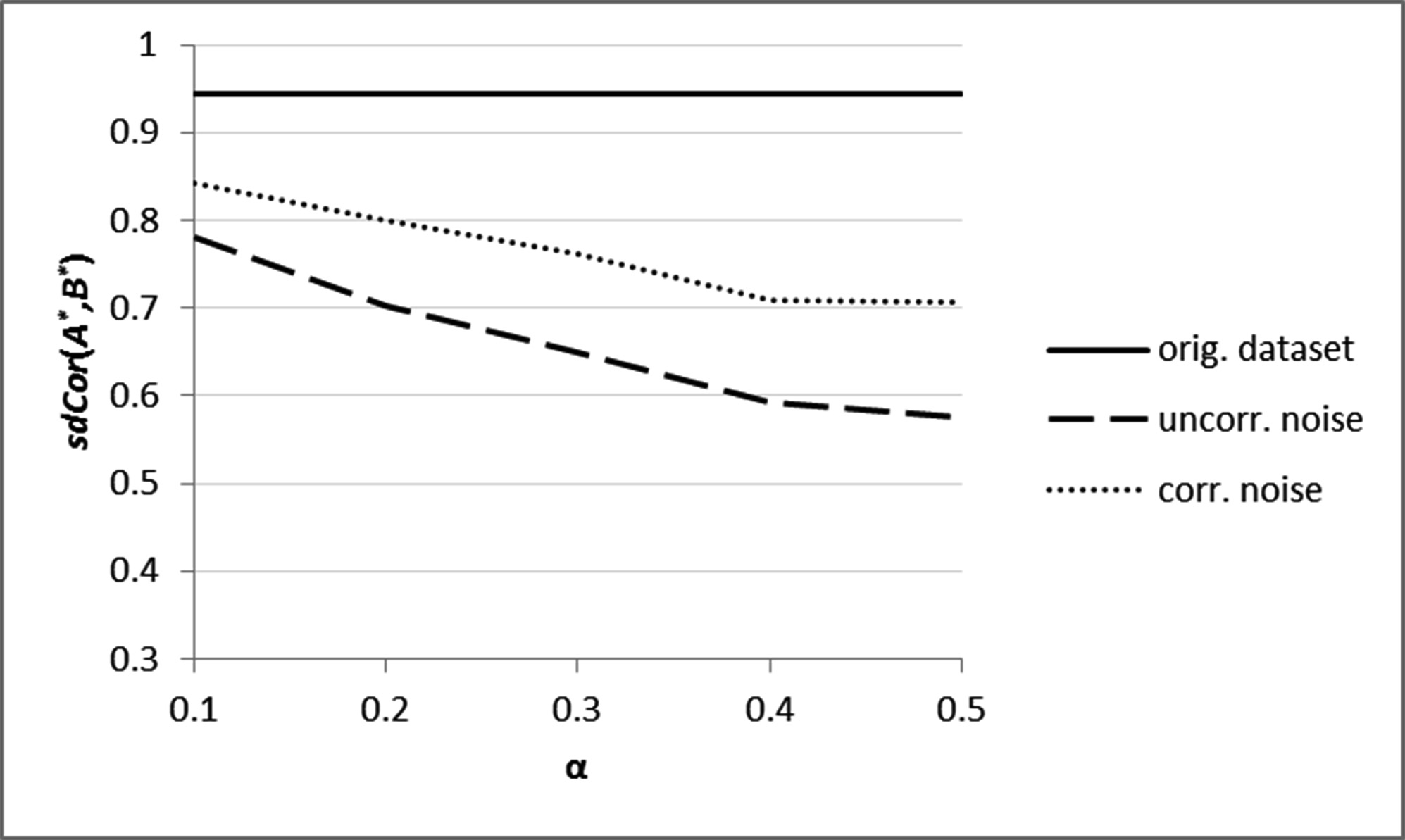
在第一个实验中，我们使用了包含1,350条记录的样本，其中两个名义属性（即A=主要诊断和B=次要诊断）之间的语义距离相关性较高（0.94）。该数据集已使用我们在第3节中提出的算法以及[16],中提出的不相关噪声添加方法进行了掩蔽，噪声参数a的常用值为=[01..0.5]。图1显示了不同方法和a取值下添加噪声的属性的语义距离相关性（sdCor，公式(11)）。正如预期，结果表明，与不相关方法相比，相关噪声添加算法能更好地保持sdCor，这种差异在 a值较大时更为明显。需要注意的是，由于以下两个原因，在向名义数据添加噪声时，语义相关性（以及如下文讨论的其他任何数据特征）无法完全保留。首先，在语义域中，值替换是离散的，而噪声幅度很少恰好匹配分类法s中的确切概念距离（特别是对于粗粒度分类法）；因此，在基于噪声的值替换过程中会累积一些近似误差。其次，由于分类法s(D(A))的大小有限，在某些情况下我们无法找到与噪声幅度所要求距离相等的替换概念；在这种情况下，将使用最远的概念作为替换，从而将噪声幅度截断为该最远概念的距离。

除了属性相关性外，噪声添加方法还应保留数据的其他特征。在[16]中表明，不相关噪声方法能够合理地保留单个属性的语义均值（sμ，公式(7)）以及保持成比例的数据离散度（sr2,，公式(8)）。我们在此提出的语义相关噪声添加方法也应保留这些特征，同时保持成比例的语义距离协方差（sdCov，公式 10）。

对于评估数据集，属性A的均值为sμ(A)=胸壁疖肿，属性B的均值为 sμ(B)=伴有肝性昏迷的病毒性肝炎，方差分别为sr2(A)= 0.22和sr2(B)= 0.24。最后，A和B之间的协方差为sdCov(A,B)= 0.2553。在表1中，我们展示了对于不同方法和a的不同取值，这些特征在添加噪声的属性中是如何被保留的。
具体而言，我们测量了每个添加噪声的属性的均值概念与原始样本均值概念之间的语义距离，以及掩码属性的实际方差/协方差与在添加噪声后期望的方差/协方差之间的绝对差异（其中a={0.2,0.4}）。在所有情况下，值为0表示均值、方差或协方差已被完全控制。此外，我们还测量了实际的均方根误差（R MSE），其计算方式为原始值与掩码值对之间的根平均平方语义距离；该指标衡量了掩码数据集中语义的整体损失，应与针对每个a所添加的噪声序列对应的目标RMSE相近。
因为a决定了添加噪声的幅度，a越大，RMSE越大（且掩码越严格）。

指标					语义不相关的噪声添加 a=0.2	语义不相关的噪声添加 a=0.4	相关语义噪声添加 a=0.2	相关语义噪声添加 a=0.4
sd(sμ(A), sμ(A*))					0.20	0.20	0	0.20
|sr2(A*) −(1+a) sr2(A)|					0.02	0.07	0.01	0.04
实际_均方根误差（A）					0.28	0.36	0.30	0.39
目标_均方根误差(A)					0.21	0.31	0.23	0.34
sd(sμ(B), sμ(B*))					0	0	0.18	0.18
|sr2(B*) −(1+a) sr2(B)|					0.05	0.09	0.05	0.08
实际_均方根误差(B)					0.24	0.34	0.28	0.37
目标_RMSE(B)					0.21	0.31	0.24	0.34
|sdCov(A*,B*) −(1+ a) sdCov(A,B)|					0.18	0.18	0.26	0.17

表1显示，实际RMSE与目标RMSE相似（即这些方法能够可控地扰动数据），尽管并不完全相同。如上所述，目标RMSE与实际RMSE之间的差异是由于需要将噪声幅度离散化和截断为分类法中的概念所致。两种方法对掩码属性均值的保持程度相似，我们无法观察到不同a值之间的显著差异。需要注意的是，尽管相关噪声添加算法更专注于保持相关性，但它在保持均值方面的能力仍能达到与非相关方法相似甚至更好的程度。表1还显示，对于这两种方法，掩码样本的方差和协方差与期望值之间的绝对差异几乎为0。这意味着相关噪声添加算法除了能更好地保持相关性外，还能像非相关方法一样有效地保持离散度。

在第二个实验中，我们提取了一个包含1,049条记录的样本，这些记录具有弱相关诊断（sdCor(A,B)= 0.24）。与上述相同，图2显示了不同方法和语义距离相关性在不同a值下的结果。在这种情况下，方法之间的差异要小得多。
这表明，对于弱相关属性，使用相关方法可能并不值得。

5 结论

在本文中，我们提出了一种基于语义的数值相关噪声添加方法，该方法能够掩盖多变量名义数据集，同时合理地保持其语义和属性相关性。与基于聚类记录的其他扰动式数据保护方法不同，我们的方案能够单独保护记录，这在保护动态数据或数据流，或需要满足个体化隐私需求时非常有用。此外，与通常用于掩盖名义值的非扰动方法（即基于泛化的方法）不同，我们的方法不会粗化数据粒度。最后，我们提出的噪声添加方法具有通用性，可支持基于噪声的数据保护方案和隐私模型（如e‐差分隐私）中常用的噪声分布（例如正态、拉普拉斯）。

作为未来工作，我们计划定义其他启发式方法来辅助值替换过程，以便在后验数据分析高度依赖某个特定特征时，能够更好地保留数据的特定特征。此外，我们还计划将我们的方法与非语义方法进行比较，例如e‐差分隐私用于分类数据的离散但面向分布的几何和指数机制。