典型相关性分析在脑电降噪的应用

关注“心仪脑”查看更多脑科学知识的分享。

关键词：科普散文、EEG

典型相关性分析

典型相关性分析（Canonical Correlation Analysis，简称CCA）是经典的统计学习方法，目标是研究两组变量之间的联系，即研究一组变量的线性组合和另一组变量的线性组合之间的线性相关关系，也就是Pearson相关系数。Pearson相关系数用于度量两个变量（X和Y）之间的相关程度，其取值在−1到1之间。它的绝对值越接近于1，则X和Y的线性相关性越高；越接近于0，则X和Y的线性相关性越低，见下图：

（来源：Wikipedia）

从图中可以清晰地看出，数据空间分布的形状与相关系数的取值呈现对应关系。

我们先假设数据向量，之后寻找一个线性组合

或者也可以理解为一组投影矩阵 和 ,用2维矩阵来描述的话如下所示：

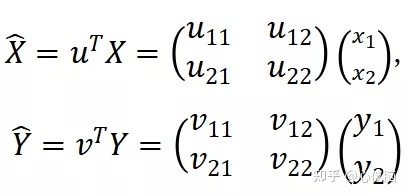
典型相关性分析的目标是寻找使得投影后的结果和的Pear