认证加密中重排序的性能优势

认证加密：重排序如何影响性能

摘要

在这项工作中，我们从一个全新的视角来研究认证加密方案。与以往仅关注构造认证加密方案的不同方法对“安全性”的影响不同，我们探讨了用于构造认证加密方案的方法对该构造的“性能”所产生的影响。我们证明，与当前美国国家标准与技术研究院标准相反，若在加密操作之前执行认证操作，则可以在不影响整体构造安全性的前提下，提高该构造的计算效率。事实上，我们证明所提出的构造甚至比基于通用哈希的标准认证更安全，因为其哈希密钥能够抵抗密钥恢复攻击。版权所有© 2017 John Wiley & Sons, Ltd.

关键词
消息认证编码；通用哈希函数族；伪随机置换；认证加密；可证明安全

1. 引言

有三种不同的通用方法可以通过将加密算法与消息认证码（MAC）算法结合来构造认证加密方案：加密并同时生成MAC（E&M）、先加密后认证（EtM）或先MAC后加密（MtE）。尽管已有大量研究致力于分析这些不同通用构造方法的安全性影响（例如，[1–6]），但针对其性能影响的研究却较少[7]。本工作特别关注当加密算法为基于分组密码、且MAC算法为基于通用哈希函数族时，此类通用构造方法的性能问题。（我们聚焦于这类构造方法，因为分组密码是构建安全加密算法的首选基本构件[8]，而基于通用哈希族的MAC是实现消息认证的最快方法[9]。）

在典型的 EtM组合中，明文被分割成块。每个块使用分组密码进行处理，生成一个密文块。然后使用基于通用哈希函数族（采用卡特‐韦格曼风格{v1}）的MAC对生成的密文块进行认证。

最近的认证加密方案之一是当前美国国家标准与技术研究院（NIST）标准化的伽罗瓦/计数器模式（GCM）认证加密 [12]。GCM 标准基于 Kohnoetal. 在[13]中提出的卡特‐韦格曼计数器（CWC）认证加密分组密码模式。GCM 和 CWC 操作模式通过将加密的计数器模式与用于认证的通用哈希函数族相结合，实现了高性能的认证加密。

最近，安全高效的认证加密算法的设计受到了越来越多的关注。继对称密码学领域长期专注的竞赛传统之后，一项新的由NIST资助的竞赛CAESAR正在征集标准化的认证加密算法。AES竞赛通常被认为极大地推动了
1997年美国国家标准与技术研究院（NIST）为新一代高级加密标准（AES）举办的公开竞赛，2004年ECRYPT为流密码（eSTREAM）举办的公开竞赛，以及2007年美国国家标准与技术研究院（NIST）为新一代哈希标准（SHA‐3）举办的公开竞赛。
版权所有 © 2017 John Wiley & Sons, Ltd. 6173

奇数密钥哈希解决方案。 在本研究中，我们探讨了加密和认证这两个操作执行顺序对性能的影响。我们描述了一种认证加密的奇数密钥哈希（OKH）模式。OKH 模式的设 计受到当前美国国家标准与技术研究院（NIST）标准（认证加密的 GCM 模式 [12]）以及 Kohno 等人[13]提出的认证加密 CWC 模式 的启发。然而，与 GCM 和 CWC 方案不同的是，OKH 模式反转了先加密后认证的顺序。也就是说，哈希操作并非应用于密文，而是在分组密码加密之前应用于明文。

早期关于认证加密系统安全性的研究结果表明，在结合一个安全的加密算法和一个安全的MAC算法时，只有EtM构造能够保证构建出安全的认证加密系统[1–3]。这些早期结果或许是将EtM构造采纳为标准的主要原因。然而，最近的研究结果表明，MtE和E&M构造实际上也能够构建安全的认证加密系统[6,7]。本工作的主要目的是突出MtE和E&M构造在性能上可能具有的优势，希望为更高效的标准制定铺平道路（特别是考虑到当前正在进行的NIST资助的竞赛以标准化认证加密算法[14]）。

本研究的主要结果是表明，在使用哈希族构造MAC时，EtM结构要求该哈希族必须是通用的，而在MtE结构中则不必如此。‘ 这一结果在性能上的意义在于，由于哈希族无需具备通用性，因此其计算速度可以比密码学文献中最快的通用哈希族更快。该结果的理论意义在于，放宽对MAC算法的安全性要求并不会影响整体认证加密结构的可证明安全性。事实上，我们证明了在抵抗[15]中发现的密钥恢复攻击（KRA）方面，MtE结构甚至比相应的EtM结构更安全。需要强调的是，本工作的主要目的并非设计最高效率的认证加密算法，而是为设计更高效的认证加密算法奠定理论基础。

在选择明文攻击下具有不可区分性的意义上是安全的。在选择消息攻击下具有不可伪造性的意义上是安全的。‘尽管相同的结果也适用于E&M组合，但为简洁起见，我们仅讨论MtE组合。

版本。本文的扩展摘要发表在第10届国际应用密码学与网络安全会议ACNS’12[16]上；这是完整版本。我们在此指出，OKH的初步版本出现在[16]中，当伪造尝试中最后一个块的整数表示等于2n–1时存在漏洞。该漏洞已在[17],中出现，并在本文中得到修复。

2. 背景和相关工作

设计认证加密系统主要有两种方法：通用方法和专用方法。在通用方法中，用于数据隐私的加密原语与用于数据完整性的MAC原语相结合，以构造认证加密系统。通用构造方法的示例包括但不限于SSH [18], IPsec[19], SSL [20],CWC [13],和GCM [12]。在专用方法中，认证加密原语被设计为一个独立的系统。首个专用方案是Gligor 和 Donescu提出的PCBC[21]。认证加密系统的形式化概念由Katz 和 Yung在[22],中以及Bellare和Rogaway在[23]中独立提出。自此以后，许多专用认证加密方案被提出，例如Katz 和 Yung的RPC[22],、Gligor 和 Donescu的XECB[24],、Jutla的IAPM[25],、Rogaway et al. [26],的OCB以及Bellare et al. [27]的EAX。值得注意的是，所有安全的专用认证加密原语都是基于分组密码的。也就是说，尽管已经提出了基于流密码的认证加密原语，例如在[28,29],中提出的方案，但这些基于流密码的提案已被分析并显示易受差分密码分析[30–33]的攻击。

使用通用哈希函数族来构造MAC算法源于 Carter 和 Wegman [10,11]。与基于分组密码的 MAC（如[34–37],）以及基于密码学哈希函数的 MAC（如[38–41], ）相比，基于通用哈希的MAC可实现更快的消息认证[42–45]。基于通用哈希的MAC的安全性已被广泛研究([15,46,47]。基于通用哈希族的MAC的速度主要依赖于所使用的通用哈希族的速度。因此，人们已投入大量努力用于

快速通用哈希族的设计。在[42],中，克拉齐克提出了密码学CRC，其哈希速度约为每字节6个周期，如肖普在[48]中所示。在[43],中，罗加威提出了桶哈希，这是首个明确针对快速软件实现的哈希族；其运行速度约为每字节1.5–2.5个周期[45]。在[49],中，约翰松描述了具有更小密钥尺寸的桶哈希。在[44],中，哈莱维和克拉齐克提出了MMH家族，其哈希速度约为每字节1.2–3个周期。在[50],中，埃策尔et al. 提出了平方哈希（square hash），这是一种MMH变体，在某些场景下可能比MMH更高效[45]。在[51],中，伯恩斯坦提出了一种基于浮点算术的哈希函数，达到了每字节2.4个周期的峰值速度。在[52],中，阿法纳西耶夫 et al. 描述了一种基于有限域上多项式求值的哈希应用。在[53],中，内维尔施滕和普雷内尔研究了为MAC设计的几种通用哈希函数的性能。面向软件实现的通用哈希函数中的速度冠军是Black et al. 在[45]中提出的 NH家族。NH家族是[44]中MMH家族的扩展。其速度提升来源于消除了MMH家族所需的非平凡模约简。NH家族的新颖之处在于它使用模2的幂的算术，或者如作者所称，“计算机喜欢执行的计算[45]”。NH家族在消息碰撞概率为2–32时，哈希速度约为每字节 0.34个周期。

最近，阿洛梅尔和普文德兰表明，与EtM组合方式不同，可以利用E&M和MtE组合方式通过省略最后一个分组密码调用[7,54]来提高系统的效率。在本研究中，我们将利用E&M和MtE组合的思想更进一步：即，在之前方案的安全性依赖于通用哈希函数的情况下，本文提出的方案无需使用通用哈希函数，从而提高了系统速度，同时仍保持所需的可证明安全性。

3. 符号与预备知识

在本节中，我们陈述了我们的假设，并描述了本文其余部分将使用的符号和定义。

3.1. 符号说明

以下符号将在本文其余部分中使用。
- 如果s是一个二进制字符串，|s|表示s的比特长度。
- 对于一个正整数 ˇ，{0, 1}ˇ表示一个长度为 ˇ 比特的二进制字符串，而{0, 1}* 表示任意长度的二进制字符串。
- 如果b是一个比特，且 ˇ 是一个正整数，则用bˇ表示将b自身连接 ˇ 次形成的比特串。
- 对于非空集合H，我们用h$ H表示从H中均匀随机选择一个成员并将其赋值给h。
- 如果x和n是正整数，且满足 0 x< 2n，我们用tostr(x,n)表示将x以大端格式表示为一个n比特的二进制字符串。
- 如果 s是一个二进制字符串，我们用toint(s)表示s的无符号整数表示（以大端格式）。
- 如果s是一个二进制字符串，且 是一个正整数，我们用setlen(s, )表示将s截断为其最高有效 比特。如果\| s\| < ，则setlen(s, )表示一个长度为 比特的字符串s||0`–|s|。

3.2. 通用哈希函数族

哈希函数族 H 由一个有限的密钥集合 K 指定。每个密钥 k 2 K 定义了该族中的一个成员 Hk 2 H。与其将 H 视为从 D 到 R 的一组函数，不如将其看作一个单一函数 H： K D! R，其第一个参数通常写作下标。随机元素 h$ H 通过均匀随机选择一个 k$ K 并令 h Hk 来确定。根据消息碰撞的概率不同（例如 [10,42,44,55–57]），存在多种类型的通用哈希族。下面我们将给出一类称为 ‐几乎通用的通用哈希族的形式化定义。

定义1。 设 H={h: D! R}为一个哈希函数族，且设 0为一个实数。若对于所有不同的M,M0 2 D，均有PrhH hh(M)= h(M0)i ，则称H是 -几乎通用的，记作 -AU。若对于所有不同且等长的字符串 M,M0 2 D，均有PrhHhh(M)= h(M0)i ，则称 H是 -几乎通用的等长字符串。

3.3. 分组密码

设F: K D! R 是一个由密钥 K索引的从 D到 R的函数族。我们用FK(D) 表示 F(K,D) 的简写。F是一个置换族（即一个分组密码），如果 D= R，并且对每个K 2 K，FK() 都是 D上的一个置换。如果F是一个置换族，我们用F–1K() 表示FK() 的逆置换，并用 F–1(, ) 表示以(K,D)为输入并计算F–1K(D)的函数。

我们采用[58]中形式化的分组密码安全性概念。令 Perm(K,D)表示密钥空间为 K、域为D的所有可能的分组密码（置换）的集合。那么，记号 $ Perm(K,D)对应于选择一个随机分组密码。给定一组函数E: K D! D和一个密钥 K 2 K，定义相关密钥预言机 ERK(, K)()为一个接受两个参数的预言机，这两个参数分别为函数 : K! K和元素M 2 D，并返回E(K)(M)。

函数 是相关密钥推导（RKD）函数或密钥变换函数。设ˆ为一组将K 映射到 K 的函数，则称ˆ 为允许的 RKD 函数集或允许的密钥变换集。

设E: K D! D为一个函数族，令ˆ为定义在 K上的一组 RKD函数。设 A为一个可访问相关密钥预言机的攻击者，且其查询请求的形式限制为(,m)，其中 2 ˆ且m 2 D。那么，

Advprp-rka ˆ,E (A)= Pr hK $K: AERK(,K)()= 1i – Pr hK $K; $Perm(K,D): ARK(,K)()= 1i

(1)

表示 A在使用ˆ限制的相关密钥将E的随机实例与随机置换区分开来时的伪随机置换（PRP）相关密钥攻击（RKA）优势。我们说 E是抗RKA的安全PRP，如果所有使用合理资源的对手的PRP‐RKA优势都很小。

如果即使攻击者获得了对逆函数的预言机访问，分组密码仍无法与随机置换区分，则称其为强伪随机置换（sprp）。然后，

Advsprp-rka ˆ,E (A)= Pr hK $ K: AERK(,K)(),E –1 RK(,K)( )= 1i – Pr hK $ K; $ Perm(K,D): ARK(,K), –1 RK(,K)= 1i

(2)

表示A在使用ˆ限制相关密钥的情况下，将 的随机实例与随机置换区分开的SPRP‐RKA优势。

3.4. 认证加密方案

我们使用的认证加密模型与[13,26]中的模型类似。一个使用nonce的对称认证加密方案AE=(K, SE, VD)包含三个算法：密钥生成算法（K），签名加密算法（SE）和验证解密算法（VD）。 AE定义在某个密钥空间KeySp、某个nonce空间NonceSp ={0, 1}nl（其中nl为正整数）以及某个消息空间MsgSp ={0, 1}*之上。我们要求能够高效地判断MsgSp中的成员关系，并且如果M、M0是两个字符串，使得M 2 MsgSp 且 |M| = |M0|成立，则应有M0 2 MsgSp。

随机化密钥生成算法 K 返回一个密钥 K 2 KeySp。确定性签名加密算法 SE 以密钥 K 2 KeySp、随机数 N 2 NonceSp 和有效载荷消息 M 2 MsgSp 作为输入，并返回密文 2{0,1}*。确定性的验证解密算法 VD 以密钥 K 2 KeySp、随机数 N 2 NonceSp 和字符串 2{0,1}* 作为输入，并输出消息 M 2 MsgSp 或在出错时输出特殊符号 INVALID。我们要求满足基本的有效性条件：如果 = SE K(N,M)，则必须有 VDK(N, ) = M。

3.5. 对抗模型

我们采用认证加密方案中使用的标准对抗模型。攻击者可以获得对签名加密算法 SEK(N,M)的预言机访问权限。攻击者可以针对她选择的随机数‐消息对(N,M)调用 SE预言机，并观察其输出。在调用 SE预言机q次后，攻击者通过调用验证解密算法VDK(N, )，对其选择的(N, )对进行伪造尝试。请注意，攻击者无法看到秘密密钥K。如果验证解密预言机返回无效符号，则认为攻击者未成功；否则，该伪造尝试被视为成功。

认证加密方案中的一个标准假设是攻击者为非重复nonce的。如果攻击者从不重复使用随机数，则称其为非重复nonce的。也就是说，在调用带签名的加密预言机查询(N,M)之后，无论预言机返回何种响应，攻击者都不会再次向其预言机提交形如(N,M0)的查询。然而需要强调的是，在伪造尝试中所使用的随机数可能与攻击者此前某次查询中使用的随机数相同。

为了对认证加密方案的隐私性进行建模，考虑一个攻击者A，其拥有两种类型的预言机之一：真实加密预言机和虚假加密预言机。真实加密预言机 EK(, )接收输入一对(N,M)，并返回密文C EK(N,M)。假设密文的长度仅取决于明文的长度，即|C| = l(|M|)。虚假加密预言机$(, )接收输入一对(N,M)，并返回一个随机字符串C$ {0,1}l(|M|)。给定攻击者A和认证加密方案 OKH =(K, SE, VD)，定义

Advpriv OKH BC,OK = Pr hK $ K: ASEK(,)= 1i – Pr hA$(,)= 1i

(3)

利用分组密码作为分组密码和哈希函数进行哈希，以破坏认证加密方案隐私性的优势 为了分析所提出系统的完整性，固定一个认证加密方案 OKH =(K, SE, VD)，并运行一个攻击者 A，该攻击者拥有针对某个密钥 K 的预言机 SEK(, )。我们采用标准的在选择消息攻击下的存在不可伪造性定义，该定义由以下游戏建模。

游戏1(EU‐CMA游戏).
(1)选择一个随机字符串K作为共享密钥。(2)假设A对一个随机数-消息对(N,M)发起带签名的加密查询。然后预言机计算完整性感知密文 = SEK(N,M)并将 其返回给 A。(3)在调用带签名的加密预言机多项式次后，A发起一次验证解密

查询(N, )。预言机计算决策d= VDK(N, ) 并将 其返回给 A。

如果攻击者 A成功伪造，当且仅当 A是随机数 尊重的，A输出一对(N, )，其中VDK(N, )¤无效， 且 A之前未发出过查询(N,M)并得到响应 。设

Advauth OKH BC,OK = Pr hK $K: ASEK(,) forgesi(4)

是 A在获得对SEK(, )算法的预言机访问权限后，针对使用BC作为分组密码进行加密且使用OK家族用于哈希的方案OKH实现成功伪造的优势。

3.6. 奇整数的性质

我们在此陈述关于有限整数环 Z2n 中奇整数的两个引理，这些引理将在本文后续部分中使用。

引理 1。 对于 Z2n 中任意非零整数 ˛ 和 ˇ，仅当 ˛ 和 ˇ 均为偶数时，2n 才能整除 ˛ˇ。形式上，以下单向蕴含必须成立：

˛ˇ 0) ˛ ˇ 0z mod 2 (5)

证明。 注意，对于任意奇数 d，gcd(d,2n) = 1；而对于任意整数 d，若 gcd(d,2n) = 1，则 d必为奇数。因此，对于任意整数 d ∈ Z2n，d ∈ Z*2n当且仅当 d为奇数。现在，设 ˛ 和 ˇ 为非零元素，并令

˛ˇ 0 (6)

但不妨假设 ˛是一个奇整数。那么， ˛在环Z2n中的乘法逆元存在。将方程 (6) 两边同时乘以 ˛–1，可推出 ˇ是Z2n中的零元素，从而通过反证法得出该引理。

引理2。 设X为从整数集合 ˚ 0, 1, 2,:::, 2n–1 中均匀随机抽取一个数 x 的实验所对应的随机变量。那么，对于任意奇整数 k 2 Z2n，随机变量Y= k X mod2n 在集合 ˚ 0, 1, 2,:::, 2n – 1 上均匀分布。

证明。 这是每个奇整数在Z2n中可逆这一事实的直接推论。为了形式化地证明该引理，只需证明对于每个y 2 ˚ 0 1 2 2 1 , 2 ˚ 0 1 2 2 1 ，，，：：：， n–，存在一个x，，，：：：，n–满足该方程

y= k x mod 2 n (7)

且这个x是唯一的。

修复任意的 y 2 ˚0，1, 2, : : :, 2n– 1 以及任意的 k ∈ Z *2 n。由于 k ∈ Z*2n，根据贝祖引理 [59],，存在 k–1 2 Z*2n使得 k–1k 1 mod 2n，两边乘以 y得 (yk– 1)k y mod 2n。因此，x=yk–1 mod 2n满足方程(7)。故存在一个 x 2 ˚0, 1, 2, …, 2n– 1满足方程(7)。

为了证明这个x是唯一的，设x0 ¤ x也满足方程(7)。那么，

x0k y mod 2n (8)

将方程(7)和方程(8)两边同时乘以k–1，得到x yk–1 mod 2n 和 x0 yk–1 mod 2n。因此，x x0 mod 2n，从而对于任意固定的y 2 ˚0, 1, 2, …, 2n– 1，满足方程(7)的 x在 ˚0, 1, 2, …, 2n– 1中是唯一的，故该引理得证。

引理1和2，以及n比特字符串与整数环Z2^n之间存在一一对应关系的事实，将被用于建立本文的结果。

4. 奇密钥哈希族

在本节中，我们将描述将在OKH认证加密构造中使用的OK哈希族。固定一个整数 n 1（“块大小”） 和一个整数 b 1（“块数”）。我们如下定义函数族 OK[n, b]：其域为D={0, 1}n [{0, 1}2n [ [ {0, 1}bn，范围为R={0, 1}n。OK[n, b]中的每个函数由b元组 K =(k1, : : :, kb) 定义，其中 ki 2 Z*₂ₙ， i = 1, : : :, b。从乘法群 Z*₂ₙ 中随机选取ki的值得到一个随机函数。由K确定的函数记作 OKK()。

对于输入消息 M2 D，将M视为一系列 n 比特块，即 M= m1 : : :m ，其中 b，并将每个块写为其在 Z2n 中的无符号整数表示（采用大端格式）。然后， M 的压缩图像由下式给出

OKK(M)= ` X i=1 kimi mod 2n (9)

当n和b的值已知时，为简化符号表示，我们将使用OK 代替OK[n,b]。

5. 奇密钥哈希认证加密的描述

如前所述，允许在GCM和CWC操作模式下实现更高 效认证的关键思想是将哈希阶段提前，应用于明文而非密文。用于加密的操作模式类似于计数器模式（ CTR），但要求对明文进行处理。

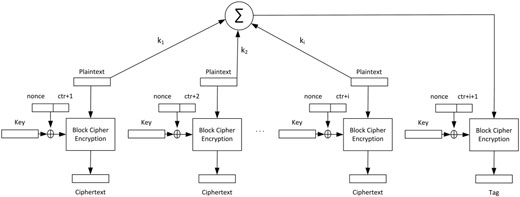
由分组密码处理。图1展示了所提出的认证加密的 OKH模式的框图。明文块与OK哈希族的密钥（即 k _i ）相乘；所得乘积对 2 ⁿ 取模求和；然后将结果通过分组密码 处理以生成标签。注意，随机数‐计数器拼接与密钥进行异或，而不是与明文块异或。因此，在非重复 nonce的对手条件下，由于使用了随机数‐计数器拼接， 每个块的加密密钥都不同于同一消息中其他所有块的 密钥，也不同于不同消息中其他所有块的密钥。这一 观察对于所提出方案的安全性至关重要。

与之前的认证加密方案（如 IAPM [25] 和 OCB[26], ）一样，我们要求分组密码 BC 是一个强伪随机置换（许多分组密码，例如 AES [61],，被认为属于强伪随机置换 [8]）。设 BC: {0,1}kl {0, 1}bs! {0,1}bs 为所使用的分组密码，其中 kl 和 bs 分别为该分组密码的密钥长度和块大小。使用 BC 进行加密、OK 家族进行哈希的认证加密方案 OKH =(K, SE, VD) 定义如下。消息空间为

MsgSp= nM 2{0, 1} *: |M| MaxLeno (10)

KeySp= n(Ke, Kh) 2{0, 1} kl {0, 1} MaxLen o (11)

NonceSp= nN 2{0, 1} *: |N| kl– log2 MaxLeno(12)

k 众所周知，重新设置密钥会影响类似高级加密标准的分组密码 的性能。另一种替代方法是用可调分组密码[60]来代替重新设置 密钥。由于特定认证加密算法的构造并不是本工作的重点；然而， 我们仅关注两种替代方案中的一种，并强调它们都能提供所需的 安全性。

其中，MaxLen 是消息的最大长度。图1操作模式中的计数器长度 CtrLen 至少为 log2 MaxLen。随机数与计数器的连接长度为 kl‐比特。

首先，明文消息的最低有效位会附加 1||0*||1。如 图2中的算法SEK(, )所示，附加零的个数取决于消息 的长度，并被选择为使得消息长度能被n整除，并且最 后一个消息块的最低有效位为“1”。非正式地说，认 证标签是通过将明文消息分割为n比特长的消息块，使 用OK家族的一个成员根据公式(9)对其进行哈希运算， 并对得到的n比特哈希值进行加密（如图3中的MAC算 法所示）来计算的。哈希结果的大小n小于或等于分组 密码的大小bs。加密部分以自然的方式执行（如图3所 示）。

备注1. 关于OK家族，有两个重要的注意事项。首先， OK家族仅在域 D上定义。然而，此问题可以通过适 当的填充轻松解决。其次，更重要的是，与通用哈希 族一样，第4节中描述的OK家族只能用于认证等长消 息。例如，全零组成的消息块不会对哈希值产生任何 贡献。因此，很容易构造出两个不同的消息发生碰撞， 最终实现成功伪造。然而，目前已有一些技术可使该 哈希函数适用于任意长度消息。例如，在[45],中，作 者提出在消息末尾附加消息长度。在我们的情况下， 只需附加序列“1||0*||1”作为消息结束(EOM)序列 （EOM中最显著位的“1”和最不显著位的“1”都将 在算法安全性中发挥关键作用，这将在定理2的证明中 详细说明）。

另一个重要说明与消息长度有关。对于长度超过 MaxLen的消息，会将其视为多个长度为MaxLen或更短的数据 块进行处理，并将相应的标签进行拼接。也就是说，任意

长消息可以使用相同的固定长度哈希密钥进行认证 （实际上，任何基于通用哈希的MAC都是如此，而不 仅仅是所提出的[45]）。通常，MaxLen被设置为一 个适当的值，既不会因最大消息长度过短而不适用， 也不会因过长而导致密钥不可行。然而需要注意的是， 这并不是一个主要的设计难题，因为通常处理的消息 长度都相对适中。例如，互联网骨干网上的消息大约 有三分之一仅为43字节[26]。为简化起见，在本文其 余部分中，我们假设消息长度不超过MaxLen。

形式上，OKH的密钥生成（K）、签名加密（SE） 和验证解密（VD）算法如图2所示。

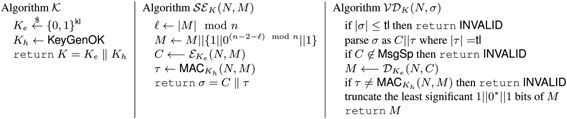
其余算法（KeyGenOK、E、 D、MAC、 OK‐HASH）在图3中定义。算法KeyGenOK负责生成密钥，以确定所使用的OK哈希函数族的成员。算法E和 D负责加密和解密操作。算法MAC负责生成认证标签，并调用算法OK‐HASH对消息进行压缩。

6. 定理陈述与证明

6.1. 加密的安全性

在本节中，我们证明了所提出的方案的隐私性是可证明安全的，前提是所使用的分组密码是抗相关密钥攻击的伪随机置换。

定理1. 设OKH[BC;OK]为第5节中描述的认证加密方案，该方案使用OK哈希族进行压缩，并使用分组密码BC进行加密。则对于任意针对OKH[BC;OK],的非重复nonce对手A，均可构造一个针对BC的攻击者B，使得

Advpriv OKH[BC;OK] (A) Advprp-rka ˚,BC(B) (13)

其中AdvprivOKH BC;OK 如公式(3)所定义， Advprp-rka˚,BC(B)表示攻击者在通过与密钥相关（密钥之间通过异或运算关联）的预言机查询条件下，破坏分组密码prp-rka安全性的优势。此外，B的实验所需时间与 A的实验相同；若 A最多进行q次预言机查询，且有效载荷数据总量不超过比特，则B最多进行/`+ q次预言机查询。

定理1指出，如果分组密码是针对相关密钥攻击安全的伪随机置换，则所提出的认证加密方案可提供数据隐私。

定理1的证明。 设B为一个针对分组密码的攻击者，该攻击者使用攻击者 A，并且能够通过预言机访问分组密码。攻击者 B运行 A，并使用自身的预言机BCRK( ,K)()来响应 A 的加密预言机查询用于第5节所述认证加密方案构造中的分组密码。攻击者B返回与 A相同的比特。然后，

Pr hK $K: ASEK(,)= 1i = Pr hK $K: BBCRK(,K)()= 1i (14)

因为在图1的操作模式中，每个块都使用不同的密钥进行加密。此外，

Pr hA$(,)= 1i= Pr hK$ K; $ Perm(K,D): BRK(,K)()= 1i (15)

因为 B使用独立选择的随机字符串来回复 A的所有预言机查询。因此，

Advpriv OKH BC;OK = Pr hK $ K: ASEK(,)= 1i – Pr hA$(,)= 1i = Pr hK $ K: BBCRK(,K)()= 1i – Pr hK $ K; $ Perm(K,D): BRK(,K)()= 1i = Advprp-rka ˚,BC(B),

定理得证。

备注2. 人们可能更倾向于选择在选择明文攻击下的不可区分性（IND‐CPA）[62],这一隐私概念，该概念描述了攻击者无法区分一对由攻击者选定的等长明文所对应的密文。然而，本文所采用的隐私定义——即攻击者无法将等长密文与随机字符串区分开来——蕴含了IND‐CPA的概念，但其逆命题不成立[26]。对于提出的OKH和遵守nonce的对手而言，由于分组密码是 prp‐rka安全的，并且在不同随机数下每个数据块都使用不同的密钥进行加密，因此IND‐CPA的安全性证明可直接得出。

6.2. 认证安全性

我们在此给出第5节方案真实性的信息论界限，该方案假设使用真正的随机置换Perm(`)进行加密。

定理2. 固定一个 OK[n,b]哈希族，并令 Perm( ): {0,1} !{0, 1} `为一个真正的随机置换，并设tl为目标标签长度。令 A为一个遵守nonce的对手，该对手提出q次查询，然后针对第5节的OKH发起伪造尝试。然后，A成功伪造的优势受到限制

Advauth OKH Perm(`),OK[n,b] 2–n+ 2–tl,

其中AdvauthOKH Perm(`),OK[n,b] 的定义见公式 (4)。

通常会引用定理2的复杂性理论类比，但在这样做时，需要访问BC–1预言机以验证伪造尝试，这相当于需要强伪随机置换假设。可得到如下结论：固定一个 OK[n,b]哈希族和一个分组密码BC : K {0,1} ! {0,1} 。设 A为一个遵守nonce的对手，其提出q次查询，总共包含至多 比特的有效载荷，然后进行其伪造尝试。则存在一个攻击该分组密码的攻击者B。

Advauth OKH BC,OK Advsprp-rka ˚,BC(B)+ 2–n+ 2–tl

此外，攻击者 B所花费的时间与攻击者 A相同，并且最多进行 /`+ q次预言机查询。

在进行安全性分析之前，我们先解释一下图1中选择OK哈希族和加密模式的直观原因。首先注意到， OK家族并不是一个通用哈希族。为了说明这一点，假设OK家族定义在环Z2n上。令M= m1||m2为由两个n比特块组成的消息（在本文其余部分中，我们重载mi以同时表示第i个消息块的n比特二进制字符串及其在大端格式下作为Z2n元素的整数表示；只要上下文清晰，这两种表示之间的区别将不再特别区分）。现在考虑消息M0= m0 1||m0 2= m1+ 2n–1||m2+ 2n–1¤M。

k1m 0 1+ k2m 0 2 = k1 m1+ 2n–1 + k2 m2+ 2n–1 (16) k1m1+ k2m2 mod 2n (17)

其中公式(17)成立，因为根据设计，k1 和 k2 均为奇整数。

备注3. 公式(17)表明，OK家族与通用哈希族不同，不能用于构造标准MAC，因为伪造者可以很容易地找到两个碰撞消息。然而，提出的OKH的一个关键思想是，找到两个碰撞消息并不等同于成功伪造（因为攻击者还必须预测出对应于碰撞消息的正确密文）。OKH设计背后的另一个关键思想是，修改观察到的密文块将导致其对应的明文块被随机修改（假设分组密码是一个强伪随机置换）。为此，以下引理分析了攻击者通过修改密文在哈希阶段引发碰撞的可能性。

引理3。 固定一个 哈希函数[n,b]哈希族，并令 P e r m( ):{0,1} !{0, 1} 为一个真正的随机置换。设 C ¤ C0为任意两个不同的密文，M ¤ M0分别为对应于 C 和 C0 的明文消息。然后，在假设使用 P e r m( )进行分组加密的情况下，Prh $哈希函数[ n,b] h h(M)= h(M0) i 2–n。

证明。 设 ci 和 c0i 分别表示 C 和 C’ 的第 i 个块。类似地，设 mi 和 m0i 分别表示 M 和 M’ 的第 i 个块。由于 M ¤ M’，它们至少在一个块上不同。假设 M 和 M0 仅在一个块上不同。不失一般性，设 m0 1= m 1+ ¤ m1，其余块均相同。由于 k1 是奇数，根据引理 1，k1 6 0 模 2n，且概率 Pr h $ 哈希函数[n,b] h h(M) =h(M0)i = 0。

假设现在M和M0的差异超过一个块。对于两个消息不同的每一个块i，记为m0i= mi+i ¤ mi。由于 Perm(`)用于加密，即使c0i与ci相差一个已知常数， i仍将是Z2n中的随机元素。因此，根据引理2，Pr h$ OK[n,b]h h(M) = h(M0)i = 2–n，引理得证。

备注4. 引理3阐明了将哈希密钥限制在奇整数集合中的重要性。为了理解这一点，假设密钥是从Z2n而非 Z*2n中选取的。假设对于某个i，ki恰好等于2n–1。那么，利用所使用的分组密码可被建模为强伪随机置换这一事实，对第i个密文块的任何修改将以1/2的概率未被检测到。这是因为对于任意偶数 ， 2n–1在模 2n下同余于零。类似地，如果对于某个i，ki恰好等于 2n–2，则对第i个密文块的任何修改将以1/4的概率未被检测到。这是因为当 是4的倍数时， 2n–2在模 2n下同余于零。一般而言，如果对于任意正整数 < n，ki等于2n– ，则对第i个密文块的任何修改将以1/2` 的概率未被检测到。

有了备注3和引理3，我们将继续进行定理2的正式证明。但在开始之前，我们先定义两种可能的对抗策略以实现成功伪造。

这两个关键思想是定理2形式化安全证明的主要组成部分。

ForgeM：给定一个明文消息M，攻击者可能试图生成一个有效的 f(M), 对，其中f是攻击者选择的函数， 是认证标签。 ForgeC：攻击者可能试图伪造一个有效的(C, )对，其中C是攻击者选择的密文， 是认证标签，而无需考虑对应于C的明文。

ForgeM 意味着攻击者试图为对攻击者有意义的特定明文消息生成有效的认证标签。ForgeC 意味着攻击者试图为某些密文生成有效的认证标签，而不管其对应的明文是什么，即使该明文最终是无意义的内容。需要注意的是，攻击者可能试图伪造她选择的消息（即 ForgeM），或某些随机消息（即 ForgeC）。因此，这两种策略涵盖了整个攻击向量。

定理2的证明。 假设 A进行了q次查询nN1, M1 , : : : , Nq, Mq o，其中对于任意i¤j均有 Ni¤Nj，并记录了该序列

S= n N1,M1, C1, 1 ,:::,Nq,Mq, Cq, q o (18)

A随后使用 N、C、 ,调用验证预言机，其中 N、 C、 6= Ni、Ci、i 对于任意i= 1，⋯，q成立，否则 A按定义无法获胜（但需注意，根据遵守nonce的对手的定义，N可以等于已记录的某个Ni）。我们此处的目标是限定 N、C、 被接受为有效数据的概率。

设M为对应于C解密的明文消息，即尝试伪造的密文的解密结果。我们的目标是限定两种可能伪造策略的概率：（i）攻击者试图为其选择的明文伪造一个有效的随机数‐密文‐标签元组（ForgeM）；或（ii）攻击者试图对某个随机数‐密文‐标签元组进行认证，而不管其对应的明文是什么（ForgeC）。

限定伪造M的概率。假设A试图对她选择的消息进行虚假认证。存在两种可能性：

(1)N¤Ni:对于任意的 i= 1, : : : , q，令 N ¤ Ni，并且回忆认证标签的计算方式为 = F N, counter, h(M) 。因此，由于 F是一个随机置换，如果 N ¤ Ni 对于任意 i成立，则预测有效标签的概率上限为 2–tl。

(2) N=Ni：令 N= Ni 对于某个 i 2 {1, ： ： ：, q}. 如果M= Mi，则只有(N,C, )=(Ni,Ci, i) 是有效的

在备注3的背景下，ForgeM 表示攻击者试图对一条与某个M发生碰撞的消息Mi进行认证，而 ForgeC 表示攻击者试图对观察到的Ci的修改版本进行认证。

已验证，根据定义攻击者不会获胜。现在，设 M ¤ Mi，并考虑以下两种情况：|M| = |Mi| 和 | M| 6= |Mi|。假设 |M| = |Mi|，并令md为 与 不同的一个密文块（由于 ¤ ，至少存在这样一个块）。令cd为对应于md的密文块。那么，要实现成功伪造，伪造者必须预测出正确的cd值。然而，请注意，根据随机数尊重属性，攻击者不能以相同的随机数和 md调用预言机来记录cd。因此，伪造的概率受限于 2–`，即预测一个随机密文块的概率。

现在，假设|M| 6= |Mi|，并考虑以下两种情况： M和Mi具有相同的块数，或M和Mi具有不同的块数。设M和Mi具有相同的块数，并回忆消息末尾会附加“1||0*||1”作为EOM序列。在这种情况下，M中EOM序列的最高有效位位置必须与它在Mi中的位置不同。令cd为对应于M中包含 EOM最高有效“1”的明文块的密文块。那么，类似于之前的情况，成功伪造的概率受限于2–`，即正确预测cd的概率。

最后，假设M和Mi的块数不同。设Mi有 ˛个块数，而试图伪造的明文M具有ˇ个块数。那么i使用密钥Ke ˚ N||tostr(˛+ 1, CtrLen) 进行加密；而为了使 通过验证，它应该是密钥Ke ˚ || + 1 ˛ N tostr(ˇ, CtrLen)对应的加密结果。由于¤≠ˇ，这两个密钥不同，并且由于i = FNi, ˛, h(Mi) 和 = FN, ˇ, h(M) ，其中F是一个随机置换，因此 与i无法相关联。此外，请注意，根据设计，EOM的最低有效位必须是最后一个消息块的最低有效位。因此， 必须是kˇ的函数，而该函数对伪造者而言是未知的。因此， 无法与观察到的Ci中的任何ci的密文块相关联。因此，攻击者成功伪造的概率受限于2–tl。

因此，从上述两种情况可知，伪造M的概率是受限的 max n2 –tl, 2– o= 2–tl 因为根据假设，tl 小于 。

限定伪造C的概率。设M和Mi分别为对应于C和 Ci的明文消息。用Coll表示事件h(M) = h(Mi)，其中 i ∈ {1, : : : , q}；即M与已记录的某个Mi发生碰撞。同时，用Coll表示Coll的补事件。

显然，这里存在两种可能的情况：要么M会与某个Mi发生碰撞，要么不会。如果对于某个i ∈ {1, : : : , q}，M与Mi发生碰撞，则 C, i ¤ Ci, i 将通过完整性检查。然而，根据引理3，通过修改密文而发生碰撞的概率为

Pr hColli= Pr hh(M)= h(Mi)i 2–n (19)

假设现在M与任何Mi均未发生碰撞。如果没有发生碰撞，则攻击者成功伪造的概率受限于预测对应于 c的明文消息的概率，或猜测对应于c的有效认证标签的概率。即

Pr hForgeC|Colli max n2–`, 2–tlo= 2–tl (20)

由公式(19)和(20)可知，伪造C的概率可以表示为

Pr hForgeCi = Pr hForgeC|Colli Pr hColli + Pr hForgeC|Colli Pr hColli (21) Pr hColli+ Pr hForgeC|Colli (22) 2–n+ 2–tl (23)

因此， A 对验证查询的成功伪造概率至多为 max nPr[ForgeM], Pr[ForgeC]o = max n2 –tl, 2–n+ 2–tl o= 2–n+ 2–tl (24)

定理得证。

备注5. 在[17],中，作者指出了此前发表于[16]的该论文初步版本存在的一种可能的伪造攻击。当最后一个消息块的偶数个数为2n–1时，此攻击有效，此时这些消息块不会对认证标签的值产生影响。本版本通过适当地对消息的最后一个块进行填充，确保最后一个消息块必须对认证标签的值产生贡献（算法 SE的第二行），从而修复了该漏洞。证明该漏洞已被修复的内容位于定理2证明中情况N= Ni的最后一段。

6.3. 抵抗密钥恢复攻击的安全性

最近，汉斯楚和普雷内尔[15]指出，与基于分组密码的MAC相比，基于通用哈希函数的MAC存在密钥恢复漏洞。原则上，对认证码进行成功伪造的概率总是存在的。然而，文献[15]表明，对于基于通用哈希函数的MAC，一旦实现了成功伪造，后续的伪造将以高概率成功。他们攻击的主要思路是寻找消息压缩阶段中的碰撞。一旦获知两个碰撞消息，就可以利用它们提取关于哈希密钥的部分信息。利用这些密钥信息，攻击者可以为伪造消息生成有效的标签。

例如，尽管OK家族在标准设置下不能用于构造安全的MACs，但假设为了说明该攻击而使用了它。设攻击者调用签名预言机于（N,M= m1||m2）以获得其认证标签 。此时，攻击者可以使用相同标签 ，调用验证预言机验证（N,M1= m2||m1）。显然，如果满足 k1 k2 mod 2n（此时有k1m1+ k2m2 k2m1+k1 m2 mod 2n），则验证将通过。

尽管验证以较小的概率通过，但攻击者可以持续使用不同的 ˛i 向验证预言机提交 (N, Mi = m2||˛im1)，直到消息被认证。设 (N, M0= m2||˛m1) 是通过验证测试的消息，其中 ˛ 2 Z2n。那么关系式 k1 ˇk2 mod 2n 将被暴露，其中 ˇ =(˛m1 – m2)(m1 – m2)–1。掌握这一信息后，中间人总能在不破坏标签的情况下，将任何未来消息 M 的前两个块 m1||m2 替换为 ˇ–1m2||ˇ m1。这是因为无论 m1 和 m2 取何值，均有 k1(ˇ– 1m2) + k2(ˇm1) = k2m2+ k1m1。

汉斯楚和普雷内尔[15]定义了通用哈希函数中的三类弱密钥。每一类都可以以类似于上述示例中讨论的方式被利用，从而在单次碰撞后显著增加成功伪造的概率。这种攻击影响所有基于通用哈希的消息认证码 [15]。根据 [15],，针对此攻击的推荐缓解措施是使用效率较低的基于分组密码的MAC，或者不对多次认证重用相同的哈希密钥。

然而，MtE结构中的消息认证码从加密算法继承了针对密钥恢复攻击的安全性。让

Advkra OKH[BC,OK] (A)= Pr hK $ K: ASEK(,) recoversi

当使用分组密码作为构造OKH的分组密码时， A成功恢复OK家族的哈希密钥的优势如下。

定理3。 固定一个 OK哈希族。设 BC是一个使用OK构造第5节中OKH的sprp-rka安全的分组密码。设 A为对 OKH发起密钥恢复攻击的攻击者。那么，存在一个攻击者 B 攻击分组密码的情况中

Advkra OKH BC,OK Advsprp-rka ˚,BC(B)

证明. 回想一下，虽然标签是明文的函数，但验证预言机接收的是密文‐标签对作为输入，而不是标准 MACs中的消息‐标签对。设(N,C, )是一个有效的随机数‐密文‐标签元组，并假设攻击者使用(N,Ci, )调用验证预言机，针对不同的Ci进行尝试，直到验证通过。根据底层分组密码的强伪随机置换‐相关密钥攻击安全性，计算受限的攻击者无法将密文与明文关联起来。因此，即使对应于C和Ci的明文M和Mi导致了碰撞，计算受限的攻击者也无法获得关于Mi的任何信息。因此，除非攻击者能够破坏所用分组密码的sprp‐rka安全性以推断出关于Mi的信息，否则无法推断出关于 OK哈希密钥的任何信息，定理得证。

7. 设计与性能讨论

在本节中，我们讨论提出的OKH方案背后的主要设计思路，并将其性能与密码学文献中的其他认证码进行比较。这种比较并非旨在表明提出的OKH是文献中最快的；其主要目的是表明此处提出的思想可能成为未来设计的一个有前景的方向。

7.1. 设计原理

首先，注意n比特序列的集合与整数环Z2n之间存在一一对应关系。因此，在对二进制序列进行算术运算时，整数环Z2n是自然的选择。从计算效率的角度来看，整数环Z2n相较于其他有限整数环具有优势，因为模约简可以通过直接截断第n位之后的比特来实现（无需复杂的模约简运算）。从数学角度来看，整数环 Z2n具有一个独特性质：当且仅当元素a ∈ Z2n为奇整数时，该元素才是可逆的。也就是说，乘法群 Z*2n由所有小于2n的奇整数组成，且仅包含这些元素。因此，对于从Z2n中均匀选取的随机数 以及奇密钥 k，值 k mod 2n在Z2n上是均匀分布的（根据引理 2）。这一事实，加上分组密码可实现为强伪随机置换的事实，构成了OKH认证加密结构设计的主要原理。即，将哈希阶段提前应用于明文，在分组密码加密之前，并将哈希密钥限制为

表I. 哈莱维和克拉齐克的MMH哈希族[44],伯恩斯坦的多项式求值（POLY）哈希族[51], Black等人提出的NH哈希族[45],以及所提出的OK家族的性能比较。

MMH家族	POLY家族	NH家族	OK家族
碰撞概率	2–30	2–96	2–64
哈希图像（比特）	32	128	128
速度（周期/字节）	1.2	2.4	0.87

奇整数集合中，可以证明，在哈希阶段通过引起碰撞来实现成功伪造的概率可以忽略不计（根据定理2）。

在文献中，通过将哈希函数限制为通用的，实现了在不提前进行分组密码加密之前的哈希阶段的情况下，确保因哈希阶段发生碰撞而导致的伪造尝试仅以可忽略的概率成功的目标。直观上，取消对哈希函数的此类限制应只会提高其速度。在表I中，我们将所提出的OK家族的速度与著名通用哈希族的速度进行了比较。

7.2. 与通用哈希函数的比较

我们在此对OK家族与Black etal提出的NH家族进行了详细的性能比较，[45],这是文献中面向软件实现的最快的通用哈希族。与其他已知哈希族的比较总结于表 I中。如前所述，设M为待认证的消息，并将M表示为一系列n比特字符串，即M= m1|| ||m ，其中\|mi\| = n。类似地，设密钥K= k1\|\| \|\|k 为哈希密钥。令 NHK为由密钥K确定的NH家族中的一个随机成员。那么，M的压缩图像计算如下

NHK(M)= `/2 X i=1 (k2i–1+ m2i–1 mod 2n) (k2i+ m2i mod 2n) mod 22n (25)

另一方面，由OK家族计算的M的哈希映像为

OKK(M)= ` X i=1 ki mi mod 2n (26)

也就是说，当块大小为n时，OK计算在Z2n上进行，而NH计算则在更大的整数环Z22n上进行。

举一个数值示例，设n= 64比特。那么，OK家族需要64位计算，而NH家族需要128位计算。在使用64位机器时，这意味着NH计算必须拆分到两个寄存器上进行，而OK计算则使用单个寄存器完成。将操作拆分到两个寄存器上 ters可能会使速度降低约63%。更重要的是，在标准编译器中，没有128位大小的整数数据类型。因此，要将两个64位整数相乘，需要将每个整数拆分为两个32位部分，并通过适当的移位进行乘法运算。在运行于UNIX操作系统的配备3.00 GHz Intel(R) Xeon(TM) CPU的64位机器上，NH家族的运行速度为0.87周期/字节，而OK家族的运行速度为0.27周期/字节。

7.3. 与当前美国国家标准与技术研究院标准的比较

在本节中，我们将简要比较所提出的OKH与Kohno等人提出的卡特‐韦格曼计数器（CWC）[13]以及其标准化版本——用于认证加密的GCM[12]。在比较过程中，我们将重点关注认证部分，因为所有这些方案都需要类似的分组密码加密。

如前所述，GCM和CWC模式都是先加密明文，然后使用通用哈希族对密文进行认证。GCM/CWC与提出的OKH之间的主要区别在于哈希阶段。在GCM和CWC中，所使用的哈希族基于伯恩斯坦的 POLY家族[51]。从表I可以看出，OK哈希族作为非通用哈希族，比文献中包括GCM和CWC认证部分所使用的POLY家族在内的最快通用哈希族还要快。

7.4. 与专用认证加密方案的比较

在本节中，我们将提出的OKH与两种著名的专用认证加密方案进行比较，即朱特拉的IAPM [25] 和罗加威等提出的 OCB [26]。首先，我们注意到，如 [13], 所述，CWC的速度与IAPM和OCB相当，在某些设置下CWC可优于它们，而在其他设置下它们则优于 CWC。其主要原因在于，IAPM和OCB在进行分组密码加密之前需要对明文块进行预处理（白化）。这种白化过程实际上是一种通用哈希函数。特别是， IAPM需要生成称为si的成对差分一致序列。每个si通过在有限域Zp上执行模乘法生成（类似于乘法运算）所有代码均使用C语言编写。

表I中MMH家族的素数更大）。在OCB操作模式中，每个消息块M[i],使用作者表示为Z[i]的字符串进行白化。每个Z[i]的计算需要生成一个格雷码 i（其中每 个 i和 i+1之间的汉明距离为1），在GF(2n)域上乘以两个多项式，然后取该乘法结果除以一个固定不可约多项式后的余数。这些多项式运算类似于表I中伯恩斯坦列出的POLY家族。

提出的OKH的另一个优势是，所有分组密码调用都可以并行执行，如图1所示。而IAPM和OCB虽然也可并行化，但至少需要三次串行分组密码调用。这是因为从第二个到倒数第二个分组密码调用依赖于第一个分组密码调用的输出，而最后一个分组密码调用依赖于之前所有分组密码调用的输出。

7.5. 密钥编排效果

值得一提的是，与上述方案不同，提出的OKH要求每个分组密码的密钥都不同。根据所使用的分组密码，由于不同的密钥编排机制，更改密钥可能会影响整个操作的性能。然而，密钥编排在不同的分组密码之间差异很大。即使在AES家族内部，AES‐128的密钥编排也不同于AES‐192，而AES‐192又不同于 AES‐256，更不用说其他AES候选算法了。此外，随着移动与普适设备的快速普及，设计适用于计算受限设备的新分组密码（例如 [63–71]）正受到越来越多的关注，其中一些设计将轻量级密钥编排作为主要目标。例如，在Light Encryption Device分组密码中就没有密钥编排[69]。因此，需要结合多种分组密码进行性能比较，才能准确评估密钥编排的影响。此外，如前所述，如果密钥重编排是一项开销较大的操作，人们可能会转而使用可调分组密码。然而，本文的主要目标是提供MAC‐then‐Encrypt相较于标准化的先加密后MAC构造可能具有的优势的理论基础。也就是说，本研究尽可能地独立于所使用的分组密码。因此，我们省略了对密钥编排影响的详细比较。

8. 结论

在本文中，我们提出了OKH认证加密方案。通过将哈希阶段提前到分组密码加密之前，我们展示了如何使用哈希函数不是通用的，可以在不影响认证安全性的前提下使用。由于该哈希函数不必是通用的，因此在密码学文献中可以比通用哈希函数计算得更快。研究还表明，对明文进行哈希而非对密文进行哈希，可以使哈希密钥在面对密钥恢复攻击时保持安全。