可验证ABKS外包方案

可验证的基于属性的关键词搜索外包

摘要

在集成广播‐宽带服务中，观众通过无线信号接收内容，同时通过互联网接收附加内容。这些附加内容可以利用每位观众的观看历史进行个性化定制。然而，观看历史包含必须谨慎处理的私有数据。可验证的基于属性的关键词搜索（VABKS）方案允许其属性满足数据所有者（观众）所指定策略的数据用户（服务提供商），在恶意云服务器上安全地搜索和访问存储的数据，并能够验证云服务器操作的正确性。然而，VABKS要求使用计算能力较弱终端（如电视机）的数据所有者执行繁重的计算任务，这是由于基于属性的加密过程所致。本文提出了一种新的VABKS方案，将这些繁重的计算外包给云服务器，从而最大限度地减轻数据所有者的计算负担。我们的方案在随机预言模型下针对两个恶意云服务器被证明是安全的：一个负责执行基于属性的加密过程，另一个负责在加密数据上执行关键词搜索过程。我们实现了本方案及先前的VABKS方案，实验结果表明，本方案显著降低了数据所有者的计算开销。

1 引言

服务提供商与用户之间的交互历史为服务提供商提供了宝贵的信息来源，可用于构建用户画像并提供与之匹配的个性化服务。然而，这些数据属于隐私信息，作为数据所有者的用户必须能够控制对这些数据的访问权限。另一方面，数据所有者通常缺乏足够的计算资源来存储和管理数据访问，因此这些操作必须委托给云服务器，而云服务器通常不可完全信任。本文聚焦于一种特定类型的服务历史，提出了一种架构，允许将用户的历史数据存储在云服务器上，并仅向用户授权的服务提供商提供访问权限，同时通过将部分计算外包给云服务器，使用户的计算开销保持在可接受水平。该架构和方法可扩展至其他广播类服务，如在线游戏和娱乐服务。

集成广播-宽带服务

集成广播‐宽带服务[5,7,8,16]允许观众通过无线信号观看内容，同时通过互联网获取附加内容。这些附加内容可用于个性化广播，并为电子商务提供机会。为了实现广播和服务的有效个性化，观众必须向服务提供商分享其观看偏好。观看历史是服务提供商了解观众兴趣的丰富数据来源。然而，这些数据可能泄露观众敏感的个人信息，因此必须谨慎处理。理想情况下，观众希望仅与满足特定条件的服务提供商共享其观看历史，例如具备可信资质或拥有基于客户评价的高评级。基于属性的加密（ABE）[2,14]使观众能够在用户终端加密其观看历史时指定策略，并将加密数据存储在云服务器中，只有属性满足该策略的服务提供商才能解密。

基于属性的关键词搜索

基于属性的关键词搜索（ABKS）[11,12,15]为数据提供基于属性的访问控制，并支持在加密域中进行关键词搜索。这使得服务提供商能够从云服务器获取所需的观看历史，同时保护观众的隐私。大多数现有的ABKS方案假设执行关键词搜索的云服务器是诚实但好奇的。郑、徐和阿特内塞[18]提出了可验证的基于属性的关键词搜索（VABKS），允许云服务器为恶意的，并给出了一个基于ABE方案、ABKS方案、数字签名方案和布隆过滤器的VABKS通用构造，从而能够验证关键词搜索结果的正确性。然而，该构造的计算成本，特别是索引生成算法的成本，对于电视机等计算能力较弱的用户终端而言过高。这是因为索引生成算法多次使用了ABE方案和ABKS方案，其带来的计算负载远高于RSA和ElGamal加密等传统公钥加密方案。

1.1 我们的贡献

本文中，我们提出了一种新的VABKS方案，其中将数据所有者（观众）的繁重计算外包给云服务器，同时能够验证计算的正确性。我们的方案在随机预言模型下针对两个恶意云服务器是可证明安全的：一个执行基于属性的加密过程，另一个对加密数据执行关键词搜索过程。我们在[18]的VABKS模型基础上增加了更多的安全要求，以适应额外的基于属性的加密过程的外包。该外包过程使得我们的方案比[18]中的VABKS方案更加高效。

具体而言，我们遵循[18]的通用构造，并使用一种属性基加密方案和一种ABKS方案，其计算可被可验证地外包。这使得我们能够构建一种具有可验证外包计算能力的VABKS方案（见图1）。对于属性基加密方案，我们将采用大竹、萨法维‐纳伊尼和张[10]提出的构造，该构造仅要求数据所有者执行ElGamal加密，并将ABE方案的繁重计算外包给云服务器。然而，据我们所知，目前尚未提出针对ABKS的外包方案。因此，为了构建一种能够将计算外包且与ABE构造兼容的ABKS方案，我们首先定义了面向恶意云服务器的安全ABKS外包模型，然后基于[15],在随机预言模型下可证明安全的ABKS方案[18]给出了VABKS外包方案的通用构造模型，并提出我们的VABKS构造，该构造使用了可外包的ABE方案[10]以及我们提出的可外包ABKS方案。

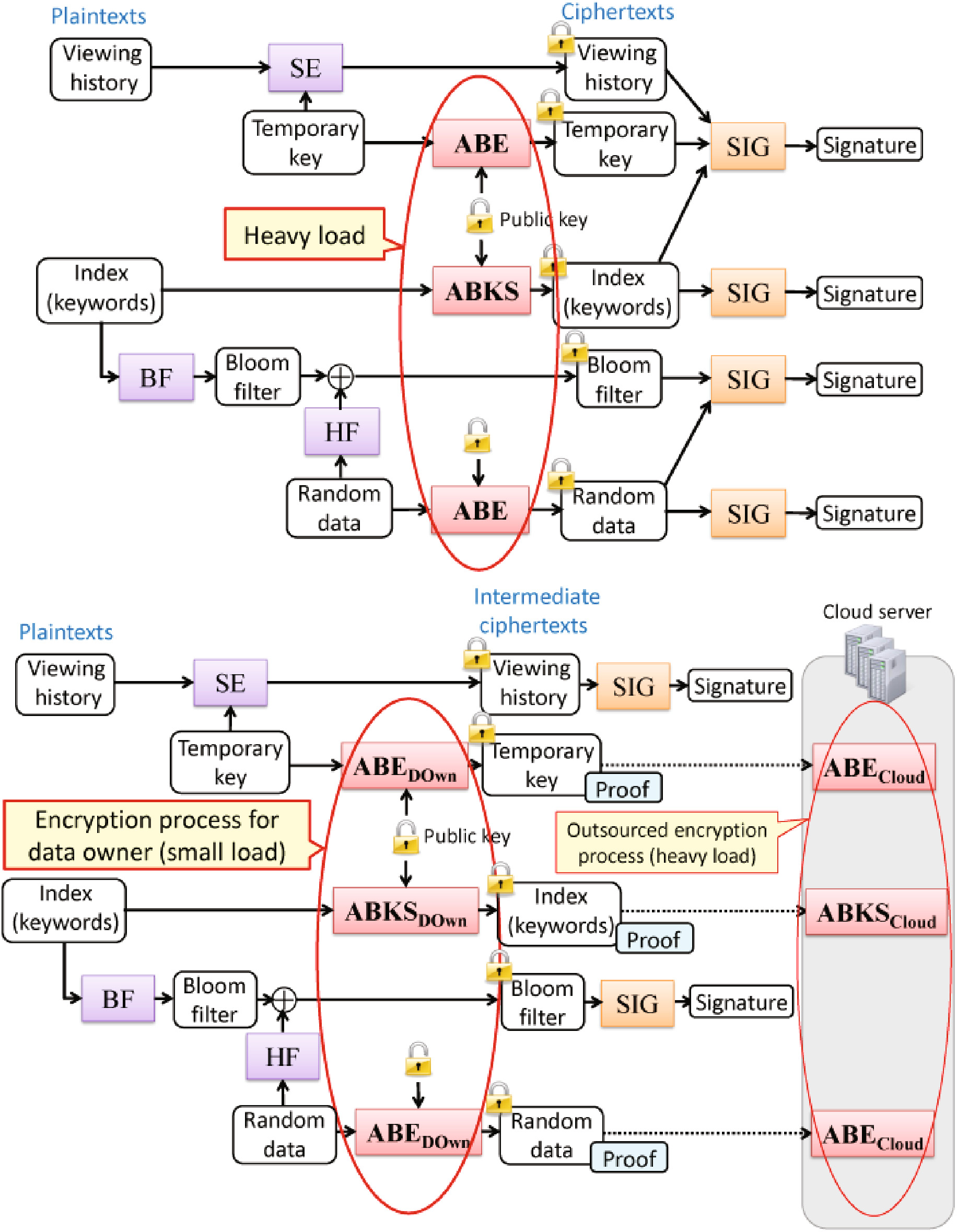
如图1所示，VABKS的通用构造[18]包含四种用于验证云服务器搜索结果正确性的签名，而我们的VABKS外包方案仅包含三种证明，这些证明通过简单使用哈希函数生成，并包含两种签名。在VABKS方案[18],中，数据用户可通过验证数据密文、加密数据的临时密钥、关键词、布隆过滤器以及用于掩码布隆过滤器的随机数据的完整性签名，来验证云服务器是否忠实地执行了关键词搜索操作。相比之下，在我们的VABKS外包方案中，数据用户可通过验证加密数据的临时密钥、关键词以及用于掩码布隆过滤器的随机数据的密文完整性的证明，来验证外包的ABE/ABKS加密过程的正确性。也就是说，签名和证明仅用于验证密文的完整性。因此，用于验证外包加密数据的证明也可用于验证搜索结果，从而可通过用证明替代部分签名来减少签名数量，这意味着我们的方案在数据所有者的签名开销方面更加高效。

最后，我们将我们的VABKS外包方案与先前的VABKS方案（未将加密过程外包给云服务器）在索引生成算法的计算开销方面进行了比较，结果表明，对于数据所有者而言，我们的方案是最高效的VABKS方案。虽然将计算外包给云服务器会增加数据所有者和云服务器的总开销，但云服务器通常配备比用户终端性能更高的中央处理器，因此在我们的方案中，索引生成算法的总体处理时间将小于先前的VABKS方案。我们还在个人计算机上实现了我们方案以及一种先前的VABKS方案的索引生成算法，实验结果显示，由于我们的方案将属性基加密和ABKS的部分加密过程外包给了云服务器，其所需处理时间仅为先前方案的一半。

1.2 相关工作

基于属性的加密及其外包

萨海和沃特斯[13]提出了第一个ABE方案，作为基于身份的加密（IBE）的扩展。ABE方案可分为（i）密钥策略ABE（KP‐ABE）[4]和（ii）密文策略ABE（CP‐ABE）[2,14]。在KP‐ABE中，密文与一组属性相关联，私钥与一个策略相关联。在CP‐ABE中，私钥与一组属性相关联，密文与一个策略相关联。当用户的属性满足密文所附带的策略时，该用户即可对密文进行解密。本文考虑使用CP‐ABE。

格林、霍亨贝格尔和沃特斯[3]首次考虑了属性基加密的外包。他们提出了一种针对属性基加密解密的外包方案，旨在最小化用户的解密成本。此后，提出了多个针对基于属性的加密的外包方案[6,9,17],，但这些方案均假设honest或honest-but-curious云服务器。相比之下，大竹、萨法维‐纳伊尼和张[10]针对云服务器为恶意的情况，提出了一种属性基加密的外包方案恶意的。在本文中，我们采用了与[10]相同的方法，并将其扩展以包含搜索功能。

基于属性的关键词搜索

ABKS将属性基加密与关键词搜索功能相结合。已提出多个ABKS方案[11,12,15],，但这些方案均假设执行关键词搜索的云服务器为诚实但好奇。相比之下，郑、徐和阿特内塞[18]提出了首个VABKS方案，假设执行关键词搜索的云服务器为恶意的，并提出了一种VABKS的通用构造，使任何人都能验证关键词搜索的结果。然而，该通用构造导致数据所有者在索引生成算法上面临较高的计算开销。本文通过采用[10]中的基于属性加密的外包（ABE外包）思想，对通用构造进行改进，并构建了一个比[18]更高效的VABKS方案。

2 预备知识

定义 1 （访问结构[1]） 。设 P={P1, P2,…, Pn}为一组参与方。 A ⊆ 2P{∅}是 P的非空子集的一个集合，如果 B ∈ A且 B ⊆ C，则 C ∈ A（∀B, C），称其为单调访问结构。 A中的集合称为授权集，不在 A中的集合称为非授权集。

在我们的场景中，属性在秘密共享方案中扮演参与方的角色。因此，访问结构 A 包含了属性的授权集。

定义 2 （线性秘密共享方案（LSSS）[14]） 。如果一个在 个参与方 P 上的秘密共享方案 Π 是线性的（在 Zp上），则称其为线性秘密共享方案，

1. 各方的份额构成一个长度为 、定义在Zp上的向量。
2. 存在一个具有 行和 n列的矩阵M，称为 Π的份额生成矩阵，以及一个函数 ρ，该函数将矩阵的每一行映射到对应的参与方。即，对于 i= 1，…， ,，值 ρ(i)是与第 i行相关联的参与方。如果我们考虑一个列向量 v=(s, r2, …, rn)，其中s ∈ Z p是要共享的秘密，而 r2, …, rn ∈ Z p是随机选择的，则 Mv是根据 Π得到的秘密 s的 个份额所组成的向量。份额(Mv)i属于参与方 ρ(i)。

在[1]中表明，每个具有上述定义的线性秘密共享方案也具有线性重构特性，定义如下：假设 Π是访问结构 A的一个LSSS。令 S ∈ A为任意一个授权集合，并令 I ⊂{1, 2,…, }按 I={i定义为： ρ(i) ∈ S}。那么存在常数{wi ∈ Z p}i∈I，使得如果{λi}是根据 Π对任意秘密{s}的合法共享，则有∑i ∈ I wiλi= s。此外，在 [1]中还表明，这些常数{wi}可以在多项式时间内相对于共享生成矩阵 M的大小被找到。

定义3 （双线性映射） 。设 G和GT是两个阶为素数 p的乘法循环群。令 g为 G的一个生成元，且 e: G × G → G T是一个满足以下性质的双线性映射：（双线性）对所有u、 v ∈ G以及 a、 b ∈ Z p ，有 e（u a, v b）= e（u, v） ab；（非退化性） e（g, g） = 1。

我们说 G是一个双线性群，如果在 G中的群运算以及双线性映射 e: G× G → GT都是可高效计算的。注意该映射 e是对称的，因为 e(ga, gb) = e(g, g)ab= e(gb, ga)。

3 系统模型

我们的VABKS外包方案的系统模型如图2所示。该模型包含五个实体：可信权威机构（TA）、数据所有者（DOwn）、两个不可信云服务器（云服务器1和云2）以及一个公共存储，其中仅云服务器1可写入该公共存储，而公共存储对公众（包括云2）是可访问的，以及数据用户（DUsr）。TA根据数据用户的属性为其分发私钥。DOwn对其数据文件及相关关键词（索引）进行基本加密，并利用云服务器1完成生成文件和关键词的基于属性的密文的剩余计算。云服务器1将结果存储在公共存储中。当DUsr希望搜索与特定关键词相关的文件时，他们为该关键词搜索创建一个令牌并将其发送给云2，云2将在加密关键词上执行搜索，并在DUsr的属性集合满足与加密关键词关联的策略时，将相应的加密文件返回给DUsr。DUsr可以验证搜索结果的正确性，并使用其私钥解密数据。

我们假设云服务器1和云2是恶意的且可能不遵守协议。

在集成广播‐宽带服务的情况下，DOwn 是持有其观看历史的观众，而 DUsr 是利用该观看历史的服务提供商

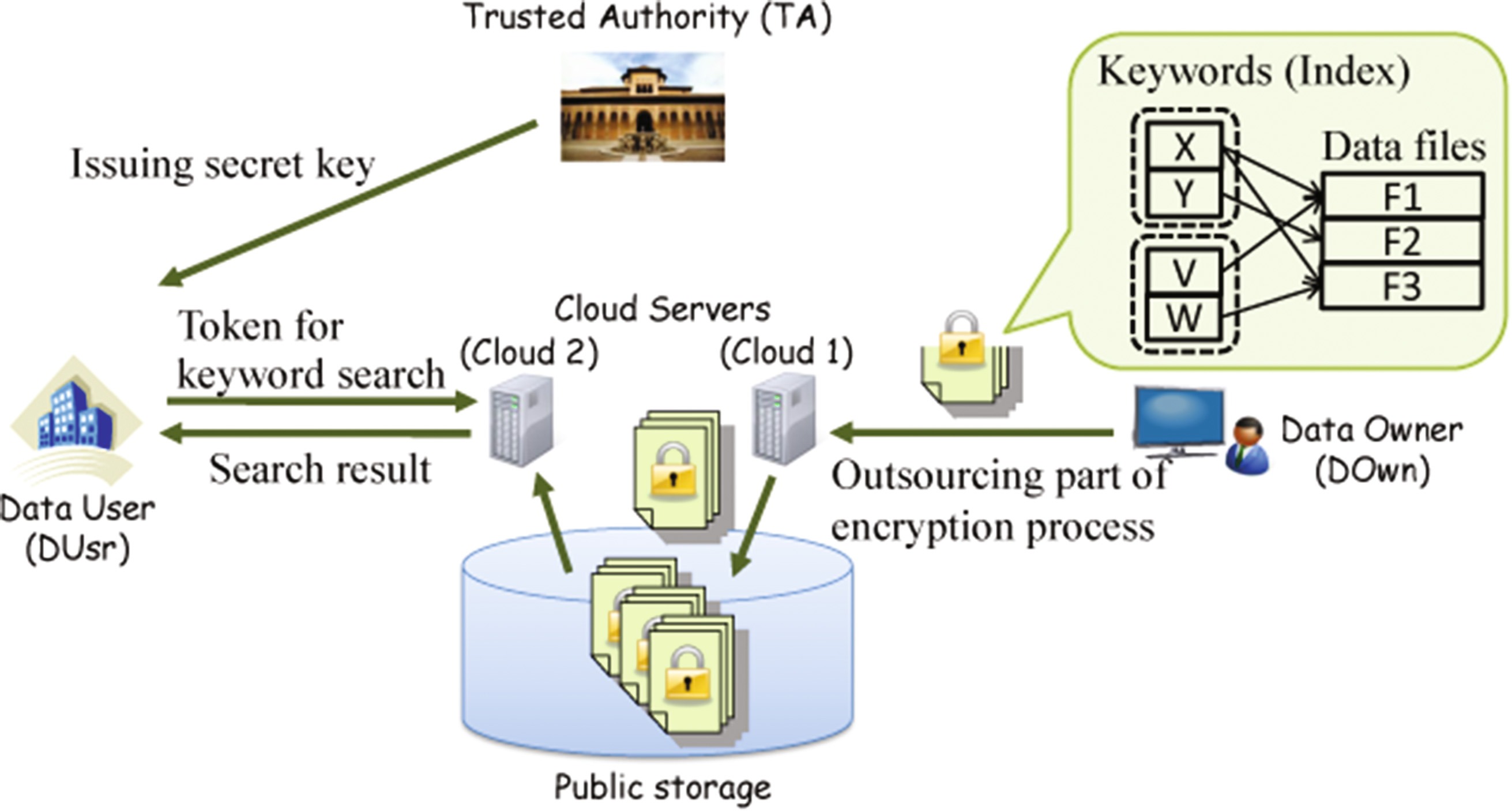
他们的服务。观看历史的索引生成给DOwn带来了沉重的负担，因此上述部分过程被外包给云服务器1。

4 ABKS外包方案

我们的基于属性的密钥搜索外包方案基于[10]中基于属性加密的外包思想。文献[18]中VABKS方案的通用构造将ABKS方案作为构建模块。特别是， VABKS方案的索引生成算法多次使用ABKS的关键词加密算法，这给DOwn带来了沉重的负担。因此，我们将部分加密过程外包给云服务器。首先，我们通过修改[18]中ABKS方案的模型和安全定义，来定义基于属性的密钥搜索外包方案的模型和安全性。之后，我们描述了我们的构造方法。为了利用线性秘密共享方案实现表达性强的策略设置，并在随机预言模型下实现可证明安全，我们方案基于[15]中的ABKS方案。

4.1 ABKS外包方案的模型

基于属性的密钥搜索外包方案的模型建立在[18],中ABKS方案的模型基础之上，其中云服务器能够判断一个加密关键词（称为“关键词密文”）是否与来自数据用户的搜索令牌相匹配。多个关键词密文可附加到一个加密数据文件上，但该数据文件不在本模型的范围之内。

ABKS外包方案的模型由七个算法组成。在此模型中，EncDOwn和EncCloud取代了[18]中ABKS方案模型的一个算法Enc。此外，该模型增加了 Verify以通过使用证明来验证搜索结果的正确性。

• (mk, pm) ← 系统初始化算法（Setup）(1) ：该算法由可信权威TA运行。输入为安全参数 1 ，输出为主密钥mk和公共参数pm。
• sk ← 密钥生成算法 （KeyGen）(mk S, pm) ：该算法由可信权威TA运行。输入为(mk, pm)和一组属性 S，输出对应于 S的私钥sk。数据用户DUsr获得私钥sk。
• (cph′, π) ← EncDOwn(w, A, ID, pm) ：该算法由DOwn运行。输入为关键词 w、访问策略 A、 DOwn的标识符ID ID以及公共参数pm，输出中间关键词密文cph′和证明 π。
• cph ← EncCloud(cph ′, pm) ：该算法由云服务器1运行。输入为cph′和公共参数 pm，输出关键词密文cph。
• tk ← 令牌生成算法（TokenGen）(sk w, id, pm) ：该算法由数据用户DUsr运行。输入为私钥sk、 w、数据用户DUsr的标识符 ID id以及公共参数pm，输出搜索令牌tk。
• ({0, 1}, aux) ← 搜索算法（ Search）(cph, tk ID, pm) ：该算法由云2运行。输入为密文cph、搜索令牌tk、 ID和公共参数pm；若满足以下两个条件：(i) S满足 A，且(ii)cph与tk对应相同的关键词，则输出(1, aux)，其中aux为用于验证搜索结果的辅助信息；否则输出(0, aux)。
• {0, 1} ← 验证算法（Verify）(cph, tk, aux π,pm) ：该算法由数据用户运行。它以密文、搜索令牌、辅助信息、 π和公共参数作为输入，若 π是密文的有效证明，则输出1；否则输出0。

4.2 ABKS外包方案的安全定义

我们通过修改[18]中ABKS方案的安全性来定义ABKS外包方案的安全性。第 4.1节中ABKS外包方案的模型是由[18]中的ABKS方案和[10],中的ABE外包方案的模型组合而成，因此我们基于[10,18]中的模型来考虑ABKS外包方案的安全性。我们假设DOwn是诚实的，DUsr是诚实但好奇的，云服务器1是恶意的，云2是诚实但好奇的，如[10]中的ABE外包方案和[18]中的ABKS方案的安全模型所述。我们定义了以下三种安全性（由于篇幅限制，省略了正式的安全定义，将在本文的完整版本中给出）：

(1) 针对选择性关键词攻击的保密性：在未提供任何匹配搜索令牌的情况下，敌手（云服务器1）无法在选择性安全模型中推断出中间关键词密文所对应的明文关键词的任何信息。该安全要求是对[18]中定义的安全性的修改：在我们方案的挑战阶段，敌手将获得一个包含中间关键词密文和证明的元组。此修改是由于将加密过程外包给了云服务器1。

(2) 关键词保密性：敌手（云2）从中间关键词密文和搜索令牌中获知关键词的概率，仅比正确随机关键词猜测的概率略微高一些。该安全要求是对[18]中定义的一种修改：在我们方案的挑战阶段，敌手获得一个包含中间关键词密文和证明以及相关令牌的元组。此修改的原因是加密过程被外包给了云服务器1（注意云服务器1和云2可能相互勾结）。

(3) 不可伪造性：给定一个中间关键词密文，敌手（云服务器1）无法创建对应于与原始关键词不同的新关键词的关键词密文。这是基于[10], notin [18]的安全要求。

上述安全定义假设破坏基于属性的密钥搜索外包方案的敌手是云服务器1和云2，且它们相互勾结。直观上，(1)和(3)是与外包给云服务器1的加密过程相关的安全性，(2)是与由云2执行的搜索过程相关的安全性。即，(1)确保云服务器1无法从DOwn发送给它的中间关键词密文中获取任何关于关键词的信息，(2)确保云2无法从DUsr发送给它的搜索令牌中获取任何关于关键词的信息，(3)确保云服务器1无法利用DOwn发送给它的中间密文来篡改关键词密文。

4.3 我们的ABKS外包方案

为了降低DOwn的计算开销，我们采用[10]的思想将部分关键词加密过程外包给云服务器1。我们的方案基于[15],中的ABKS方案，该方案通过使用LSSS实现表达性强的策略设置，并且在随机预言模型下可能是可证明安全的（尽管[15]中未提供安全证明）。

系统初始化算法（Setup）(1) ：可信权威选择一个素数阶的双线性群 G ，一个双线性映射 e: G × G → GT，一个生成元 g 属于 G，哈希函数 H: {0, 1}∗ → G，H′: {0, 1}∗ × GT ×{0, 1}∗ →{0, 1}∗， H′′: {0, 1}∗ →{0, 1}∗， 以及一个消息认证码函数 F: GT ×{0, 1}∗ →{0, 1}m，其中 m 是消息认证码的长度。它还选择随机数 α、 a ∈ Zp。可信权威设置公共参数和主密钥为 pm == 〈g, ga, e(g, g)α, F(·,·) H(·) H′(·,·,·) H′′(·)〉 和 mk == α。

密钥生成算法（KeyGen）(mk, S, pm) :数据用户将它的标识符ID id和一组属性 S发送给可信权威。可信权威选择一个随机值 t ∈ Zp，生成 K= gαgat、 L= gt以及{Kx= H(x)t}x∈S，并在用户列表中添加一项(id, gat)。可信权威将私钥设置为sk = 〈K, L,{Kx}x∈S〉，并将其发送给数据用户。

EncDOwn(w, (M, ρ), ID, pm) ：这是一个使用策略(M, ρ)加密关键词w的算法。其中， M是一个访问矩阵， ρ是一个将 M的行与属性相关联的函数。DOwn随机选择 s, y2, …, yn,β1, β2, …, βn ∈ Zp，并设置一个列向量 v=(s+ β1, y2+ β2, …, yn+ βn) ∈ˆZ n p。然后计算 C′= gs和 k= e(g, g)αse(g, H(w))s。接着，选择一个随机比特串ˆt，并设置关键词 w的索引： idx(w)=(ˆt, F(ˆk, ˆt))。之后，计算一个证明 π= H′(ID, ˆk, H′′(posM))。其中， ID是DOwn的标识符ID，posM是一个包含访问矩阵 M中所有值为1的位置的字符串。例如，如果矩阵 M为

M=(0 1 1 1),

则posM={(1,2),(2,1),(2,2)}。对于 1 ≤ i ≤ ,，令 Ji为集合 Ji={j： Mij=1(1 ≤ j ≤ n)}。DOwn计算 Ei= g a∑ j∈ J i β j并将中间密文设为cph′= 〈C′, (Ei)1≤i≤, v,(M, ρ) idx(w)〉。它将(ID, cph′, π)发送给云服务器1。

EncCloud(cph ′, pm) :对于 1 ≤ i ≤ ,云服务器1 计算 λi= Miv，其中 Mi 是对应于 i行的 M 的行向量。此外，它选择随机数 r1, …, r ∈ Z p。然后计算

Ci= g aλ iH(ρ(i)) −r i Ei , Di= g r i(1 ≤ i ≤ )

并设置密文为 cph = 〈C′,(Ci , D i) 1 ≤i≤ ,(M, ρ) idx(w)〉。云服务器1 将 (ID, cph, π) 存储在公共数据库中。

TokenGen(sk, w, id, pm) :数据用户选择一个随机值 u ∈ Z p 并计算 qu = g u。它将id和 qu 发送给可信权威。然后，可信权威根据 id检索 g at ，生成 qid = g at q α u ，并将 其发送给数据用户。数据用户计算

Tq(w) = H(w)q1/u id, L′= L1/u，以及 Kx′= K1/u x(∀x ∈ S)，并设置搜索令牌为 tk = 〈Tq(w) L′,{Kx′}x∈S〉。它将该令牌发送到云2。

搜索算法（Search）(密文, 搜索令牌, , 公共参数) : 云2 输出 (0, ⊥)，如果 S 不满足 (M, ρ)。否则，令 I ⊂{1, 2,…, } 定义为 I={i: ρ(i) ∈ S}，且 {μi ∈ Zp}i∈I 为一组常数，使得若 {λi} 是根据 M 得到的任意秘密 s 的有效份额，则有 ∑i∈I λiμi= s。然后，云2 计算

aux1=∏ i∈I( e(Ci, L′)e(Di, K′ ρ(i))) μi , k= e(C′, Tq(w)) aux1 .

云2 设置辅助信息 =(aux1, ID)。如果 F(k, ˆt) = F(ˆk, ˆt)，云2 输出 (1, aux)；否则， 输出 (0, aux)。

验证算法（Verify）(cph, tk, aux, π pm) :数据用户输出 0，如果 aux = ⊥。否则，输出 1 如果 π= H′(ID, e(C′, Tq(w)) aux1 , H′′(posM)). 否则，输出0。

备注1 . 如果DOwn保留了在EncDOwn算法中生成的随机数 s，则其能够验证公共数据库中存储的(ID, cph, π)元组的正确性。也就是说，即使云服务器1从头创建另一个(ID, cph∗, π∗)元组并将其存储在公共数据库中，DOwn也能检测到该攻击行为（尽管这要求DOwn定期检查数据库的状态）。

Theorem 1 . 上述ABKS外包方案的安全性如下 s:

• 在随机预言模型中，如果决策性 q-并行DBHE假设成立，则该方案针对选择关键词攻击是选择性安全的。
• 在随机预言模型中，如果 H是单向哈希函数，则该方案具有关键词保密性。
• 在随机预言模型中，如果 H具有抗碰撞性，则该方案是不可伪造的。

我们由于篇幅限制省略了定理1的证明（我们将在本文的完整版本中给出）。

5 可验证基于属性的关键词搜索外包方案

[18]中的VABKS通用构造由属性基加密、ABKS、数字签名和布隆过滤器组成。然而，与RSA和ElGamal加密等传统公钥加密方案相比，属性基加密和ABKS带来了更重的计算负担。特别是使用属性基加密和ABKS进行的关键词加密过程由DOwn执行，而DOwn的设备（例如电视机）可能具有低性能的中央处理器。为了减轻此类设备的负担，我们设计将DOwn执行的属性基加密和ABKS部分加密过程外包给云服务器1。

5.1 可验证基于属性的关键词搜索外包方案模型

设 FS ={F1,…,Fn} 为一组数据文件。令 KGj(1 ≤ j ≤ l) 为一组关键词（称为关键词组），这些关键词将使用访问策略Aj进行加密。即， A1, …, Al 分别被分配给 KG1,, …,KGl。令 KG ={KG1,…,KGl}。对于每个关键词 w，令 MP(w) 表示包含关键词 w 的数据文件的标识符ID集合。令 MP ={MP(w) |w ∈ ⋃l i=1KGi}。令 D =(KG, MP,FS) 表示带有关键词和标识符ID的数据文件。

VABKS外包方案由以下七个算法组成。在此模型中，BuildIndexDOwn和 BuildIndexCloud替换了BuildIndex，即VABKS方案模型中的一个算法，如[18]所示。

• (mk, pm) ← Init(1) ：该算法由TA运行。输入为安全参数 1，输出主密钥 mk和公共参数pm。
• sk ← KeyGen(mk S, pm) ：该算法由TA运行。输入为(mk, pm)以及DUsr的一组属性 S，输出对应于 S的私钥sk。
• (Au′, Index′, D′ cph) ← BuildIndexDOwn({A}l,{A′}n, D, pm) ：该算法由DOwn运行。输入为一组用于加密关键词组KG1,…, KGl的访问策略 {A}l={A1,…, Al}，一组用于加密数据文件FS1,…, FSn的访问策略 {A′}n={A′ 1,…, A′ n}，数据D以及pm。输出中间辅助信息Au′、包含与数据文件相关的加密关键词的中间索引密文Index′，以及包含加密数据文件的中间数据密文D′ cph。
• (Au, Index, Dcph) ← BuildIndexCloud(Au ′, Index′, D′ cph, pm) ：该算法由云服务器1运行。输入为Au′、Index′、D′ cph和pm，输出辅助信息Au、索引密文Index以及数据密文Dcph。
• tk ← TokenGen(sk w, pm) ：该算法由DUsr运行。输入为sk、一个关键词 w和pm，输出搜索令牌 tk。
• (rslt, proof) ← SearchIndex(Au, Index, Dcph, tk, pm) ：该算法由云2运行。输入为Au、Index、Dcph、tk和pm，输出搜索结果rslt和证明 proof。
• {0, 1} ←Verify(sk w, tk, rslt, proof, pm) ：该算法由DUsr运行。输入为sk、 w、tk、rslt、proof和pm，若(rslt, proof)有效则输出1，否则输出0。

5.2 VABKS外包方案的安全定义

VABKS外包方案的安全性是对[18]中定义的VABKS方案安全性的修改。我们假设 DOwn是诚实的，DUsr是诚实但好奇的，而云服务器1和云2是恶意的。需要注意的是，在第4.2节ABKS外包方案的安全性定义中，云2被假定为诚实但好奇的。这是因为在基于属性的密钥搜索方案中，执行关键词搜索的云服务器被假设为诚实但好奇的，该方案可作为构建VABKS方案的构件之一（参见[18]）。我们定义四种安全，如下所述（由于篇幅限制，我们省略了正式的安全定义，将在本文的完整版本中展示）：

(1) 数据保密性：给定加密关键词和搜索令牌后，敌手（云2）无法获得关于数据文件的任何信息。该定义可形式化为一个选择明文安全游戏，其中两个挑战 D0=(KG, MP, FS0)和D1=(KG, MP, FS1)对应相同的KG和MP，且 |FS 0| = |FS1|。此安全要求与[18]中的相同。

(2) 针对选择性关键词攻击的保密性：与ABKS的选择性安全抵抗选择关键词攻击相同（见第4.2节）。

(3) 关键词保密性：与ABKS的关键词保密性相同（见第4.2节）。

(4) 可验证性：如果敌手（云服务器1）非法修改了关键词密文，或敌手（云2）返回了错误的搜索结果，则数据用户能够以压倒性概率检测到该行为。该安全定义是对[18]中可验证性的改进：在本方案的设置阶段，敌手可以获得一个包含中间索引密文、中间数据密文以及中间辅助信息的元组。这一修改是由于将加密过程外包给了云服务器1。

在上述安全定义中，我们假设试图破坏VABKS外包方案的敌手是云服务器 1和云2，并且它们相互勾结。(2)和(4)与外包给云1的加密过程相关，而(1)、(3)和(4)与由云2执行的搜索过程相关。具体而言，(1)确保云2无法从公共存储中的关键词密文以及数据用户发送给它的搜索令牌中获取任何数据文件的信息，(2)确保云1无法从DOwn发送给它的中间关键词密文中获取任何关键词信息，(3)确保云2无法从数据用户发送给它的搜索令牌中获取任何关键词信息，而(4)确保云1不能修改关键词密文，且云2不能通过使用DOwn发送给它的中间密文来篡改搜索结果。

5.3 我们的VABKS外包方案

我们通过将[18]中的VABKS通用构造与将基于属性的加密过程外包给云服务器 1的思想相结合，构建了我们的VABKS外包方案。具体而言，我们在[18]的 BuildIndex算法中，用[10]中ABE外包方案的Encryptu替换ABE.Enc，并用第4.3节中ABKS外包方案的EncDOwn替换ABKS.Enc。这些外包过程降低了DOwn的计算开销。此外，在[18],的BuildIndex算法中生成了四种签名，给 DOwn带来了较大的负载。因此，我们尝试利用ABE外包方案和ABKS外包方案 中的证明机制，尽可能减少这些签名的数量。

初始化(1 ) : 给定安全参数 ,，可信权威TA 选择 k 个通用哈希函数 H′ 1 , …, H′ k ， 用于构造一个 m‐位的布隆过滤器。

令 H ：{0, 1} →{0, 1}m 是一个安全的伪随机生成器，SE 为一个安全的对称加密方案，Sig 为一个安全的签名方案，ABEO 为 [10], 中的 ABE 外包方案， ABKSO 为第4.3节中的 ABKS 外包方案。可信权威 TA 执行 (ABEO.pm, ABEO.mk) ← ABEO.Setup(1) 和 (ABKSO.pm, ABKSO.mk) ← ABKSO.Setup(1)。它将公共参数和主密钥设置为 pm =(ABEO.pm, ABKSO.pm H1′, …, Hk′) 和 mk = (ABEO.mk, ABKSO.mk)。

密钥生成算法（KeyGen）(mk S,pm) : 可信权威 TA 运行 ABEO.sk ←ABEO.KeyGen(ABEO.pm, ABEO.mk, S) 和 ABKSO.sk ←ABKSO.KeyGen (ABKSO.pm, ABKSO.mk, S)，设置 sk = (ABEO.sk, ABKSO.sk)，并通过经过认证的私有信道将 sk 发送给数据用户 DUsr。

BuildIndexDOwn({A}l,{A′}n,D,pm) : 数据拥有者 DOwn 执行 (Sig.sk, Sig.pk) ← Sig.KeyGen(1)，保留 Sig.sk 的私密性，并公开 Sig.pk。给定 D =(KG={KG1, …, KGl}, MP={MP(w) | w ∈⋃ l i=1 KGi}, FS ={F1, …, Fn})，DOwn 执行以下操作：

1. 使用混合加密对每个数据文件进行加密： ∀Fj ∈ FS，通过运行 SE.skj ← SE.KeyGen(1) 生成中间密文 cph′ Fj =(cph′ skj , cphSEj)，cphSEj ← SE.Enc(SE.skj, Fj)，以及 (cph′ skj , πskj) ←ABEO.Encryptu(pm, IDDOwn, A ′ j, SE.skj)，其中 IDDOwn是 DOwn 的标识符ID。此外，生成 σSEj ← Sig.Sign (Sig.sk, cphSEj)。
2. 加密每个关键词：给定 KGi, 1 ≤ i ≤ l，对于每个 w ∈ KGi，执行 (cph′ w, πw) ← ABKSO.EncDOwn(w, Ai, IDDOwn, pm)，并设置 MP(cph′ w)={IDcph′ F j |IDF j ∈ MP(w)}，其中 IDF j和 IDcph′ F j分别是用于标识数据文 F j 的标识符ID。
3. 为每组 KGi生成一个布隆过滤器：令 BFi ← BFGen({H′ 1,…, H′ k}, KGi)，(cph′ BFi , πBFi) ← ABEO.Encryptu(pm, ID DOwn, Ai, M)，其中 M 从 ABEO 的消息空间中随机选择，计算 BF′ i= H(M) ⊕ BFi，并生成 σBFi ← Sig.Sign(Sig.sk, BF′ i)。
4. 令 Au′=(IDDOwn, cph ′ BF 1 , …, cph′ BF l , σBF1 , …, σBFl , σSE 1 , …, σSEn , πsk 1 , …,πskn ,{πw|w ∈⋃ l i=1KGi}, πBF1 , …, πBFl , BF′ 1, …, BF ′ l)，Index′=({cph′ w|w ∈⋃ l i=1 KGi},{MP(cph′ w)|w ∈⋃ l i=1 KGi})，以及 D′ cph =({cph′ F j |Fj ∈ FS})。

BuildIndexCloud(Au ′, Index′, D′ cph , pm) ：云服务器1 运行 cphsk j ← ABEO.Encryptc(pm, cph′ sk j )，cphw ← ABKSO.EncCloud(cph ′ w, pm)，以及 cphBFi ←ABEO.Encryptc(pm, cph′ BF i )。设置 MP(cphw) ={IDcph F j | IDcph ′ F j ∈ MP(cph′ w)}。令 Au =(IDDOwn, cph BF 1, …, cph BF l, σBF1 , …, σBFl , σSE 1 , …, σSE n , πsk 1 , …, πsk n ,{πw|w ∈⋃ l i=1 KGi}, πBF1 , …, πBFl , BF′ 1, …, BF ′ l)，Index =({cph w|w ∈⋃ l i=1 KGi},{MP(cphw)|w ∈⋃ l i=1 KGi})，以及 Dcph =({cphF j |Fj ∈ FS})。

令牌生成算法（TokenGen）(sk, w, pm) ： 数据用户生成一个搜索令牌tk ← ABKSO.TokenGen(ABKSO.sk, w, ID D Usr , pm)，其中ID D Usr 是数据用户的标识符ID。

SearchIndex(Au,Index,Dc p h,tk,pm) : 令结果列表rslt和证明proof初始为空集。云2枚举∏i ={cphw |w ∈ KGi} , 1 ≤ i ≤ l，即具有相同访问控制策略的关键词密文。

• 对于每个密文cphw ∈ ∏i，运行(γ, aux) ← ABKSO.搜索(cphw, tk, 标识符I DDOwn, pm)。如果 γ= 0，则继续处理 ∏i中的下一个关键词密文。如果γ= 1，则将元组(标识符IDDOwn, cphw,{cphFj|标识符IDcphFj ∈主参数(cphw)})添加到结果列表rslt中，并将(πw,cphBFi)添加到证明proof中。
• 如果在处理完 ∏i 中的所有密文w后没有 γ= 1，则将 (BF′ i, 密文BFi, σBFi, πBFi) 添加到证明中。

验证算法（Verify）(sk w,tk, rslt,证明, pm) : 数据用户通过以下方式验证来自云2的搜索结果：

1. 对于 i= 1,…, l，验证云确实返回了每个关键词组 i的正确结果，具体如下：
   - 情况1 ：如果 (IDDOwn, cphw,{cphFj|IDcphFj ∈MP(cphw)}) ∈rslt，表示存在一个关键词密文 cphw，其对应的访问控制策略与 cphBFi 所指定的相同，并且具有搜索令牌 tk 所指定的相同关键词，则执行 (γ, aux) ← ABKSO.Search(cphw, tk, IDDOwn, pm) 和 γ′ ← ABKSO.Verify(cphw, tk, aux, πw, pm)，以验证 cphw 是否与 tk 匹配且未被篡改。如果任一验证失败 γ= 0 或 γ′= 0，则返回 0。否则，执行 {SE.skj/ ⊥} ←ABEO.Dec(cphskj, πskj, ABEO.sk, pm, IDDOwn)。如果输出为 ⊥，则返回 0。否则，执行 γ′′ ← Sig.Verify(Sig.pk, σSEj, cphSEj)。如果 γ′′= 0，则返回 0；否则，继续执行 i= i+ 1。
   - 情况2 ：如果(BF′ i,cphBFi, σBFi, πBFi) ∈proof，表示不存在匹配的关键词密文，则继续通过运行 γ′ ← Sig.Verify(Sig.pk, σBFi, BF ′ i)来验证被掩码的布隆过滤器的完整性。如果 γ′= 0，则返回0；否则，执行以下操作：
   • 如果数据用户DUsr被授权，则计算{M/ ⊥}← ABEO.Dec(cphBFi, πBFi , ABEO.sk, pm, IDDOwn)。如果输出为 ⊥，则返回0；否则，BFi= H(M) ⊕BF ′ i。执行 δ ← BFVerify({H′ 1,…, H′ k}, BFi, w)以检查 w是否存在于由BF{v17}表示的关键词组中。如果 δ= 0，意味着 w 不在由布隆过滤器 BFi 表示的关键词组中，则继续执行 i= i+ 1。
   • 如果 δ= 1，则从云2下载 ∏i={IDDOwn,(cphw, πw)|w ∈KGi}。然后，在 {cphw|w ∈KGi}中枚举 cphw，执行 (τ, aux) ← ABKSO.Search(cphw, tk, IDDOwn, pm) 和 τ′ ←ABKSO.Verify(cphw, tk, aux, πw, pm)。如果处理完所有 cphw后存在某个 τ′= 0（表示密文被修改），返回 0；否则，如果处理完所有 cphw后存在某个 τ= 1（表示存在与 tk 匹配的 cphw），返回 0；否则，继续执行 i= i+ 1。
   • 如果数据用户未授权，则继续执行 i= i+ 1，因为密文BF i无法被解密。
   • 情况3 ：如果上述情况均未发生，则返回0。
2. 如果搜索结果中的所有元组都已成功验证，则返回1，否则返回0。

Theorem 2 . 我们VABKS外包方案的安全性如下：

• 如果ABEO和SE能够抵抗选择明文攻击，则该方案实现数据保密性。
• 如果ABEO能够抵抗选择明文攻击， H是一个安全的伪随机生成器，且 ABKSO能够抵抗选择关键词攻击，则该方案是选择性安全的。
• 如果ABEO能够抵抗选择明文攻击，H是一个安全的伪随机生成器，且ABKSO实现关键词保密性，则该方案实现关键词保密性。
• 如果Sig、ABEO和ABKSO均不可伪造，则该方案实现可验证性。

我们由于篇幅限制省略了定理 2的证明（我们将在本文的完整版本中给出）。

6 比较

表1比较了我们的VABKS外包方案与先前的VABKS方案在DOwn计算开销方面的差异。在此表中， MG和MGT分别表示在 G和 GT中一次模幂运算的计算开销， P表示椭圆曲线上的配对运算一次的计算开销，表示策略中的属性数量 （也是访问矩阵的行数）， l表示关键词组的数量， nw表示所有关键词组中的关键词总数， n表示数据文件的数量。ABE.Enc和ABKS.Enc分别表示一次 ABE加密和一次ABKS加密的计算开销。ZXA‐1表示在通用构造[18]中使用[2] 中的CP‐ABE方案和[18]中的CP‐ABKS方案的VABKS方案。ZXA‐2表示在通用构造[18]中使用[14]中的CP‐ABE方案和[15]中的CP‐ABKS方案的VABKS方案。Ours表示第5.3节中的VABKS外包方案。DOwn执行ABE n+ l次和 ABKS nw次，因此ZXA‐1、ZXA‐2和Ours的总加密成本分别为((2+ 1)n+( 2+ 1)l+(2+ 4)nw)MG+(n+ l)MGT、((3+1)n+(3+1)l+(3+1)nw) MG+(n+ l+2nw)MG T + nwP和((+1)n+(+1)l+(+1)nw)MG+(n+l+2nw) M G T +nwP。例如，在 = 5, n= 10, l= 1,和 nw= 30的情况下，ZXA‐1、 ZXA‐2和Ours的总成本分别为 541MG+ 11MG T 、 656MG+ 71MG T +30P和 246MG+ 71MG T +30P。ZXA‐2和Ours需要nw次配对运算，因此它们的成本高于ZXA‐1。然而，尽管ZXA‐1在通用群组模型中是可证明安全的，ZXA‐2和 Ours则在随机预言模型中是可证明安全的。因此，在这一更现实的假设下， Ours在DOwn的加密成本方面是最高效的VABKS方案。

ZXA‐1、ZXA‐2 和 我们的方案 分别使用 2l+ nw+ 1、 2l+ nw+ 1 和 l+ n 个 签名。例如，在 n= 10、 l= 1 和 nw= 30 的情况下，ZXA‐1、ZXA‐2 和 我们的方案 分别使用 33、33 和 11 个签名。因此，我们的方案 使用的签名数量更少。

另一方面，在 我们的方案 中，部分签名被证明所替代，证明的数量为 n+ l+ n w。在 n= 10、 l= 1 和 n w= 30 的情况下，证明的数量为 41，这比签名数量更多

）)

ZXA‐1和ZXA‐2中的签名。然而，可以通过使用哈希函数以比数字签名方案更低的计算开销生成证明。这意味着在DOwn的签名开销方面，我们的方案是效率最高的VABKS方案。

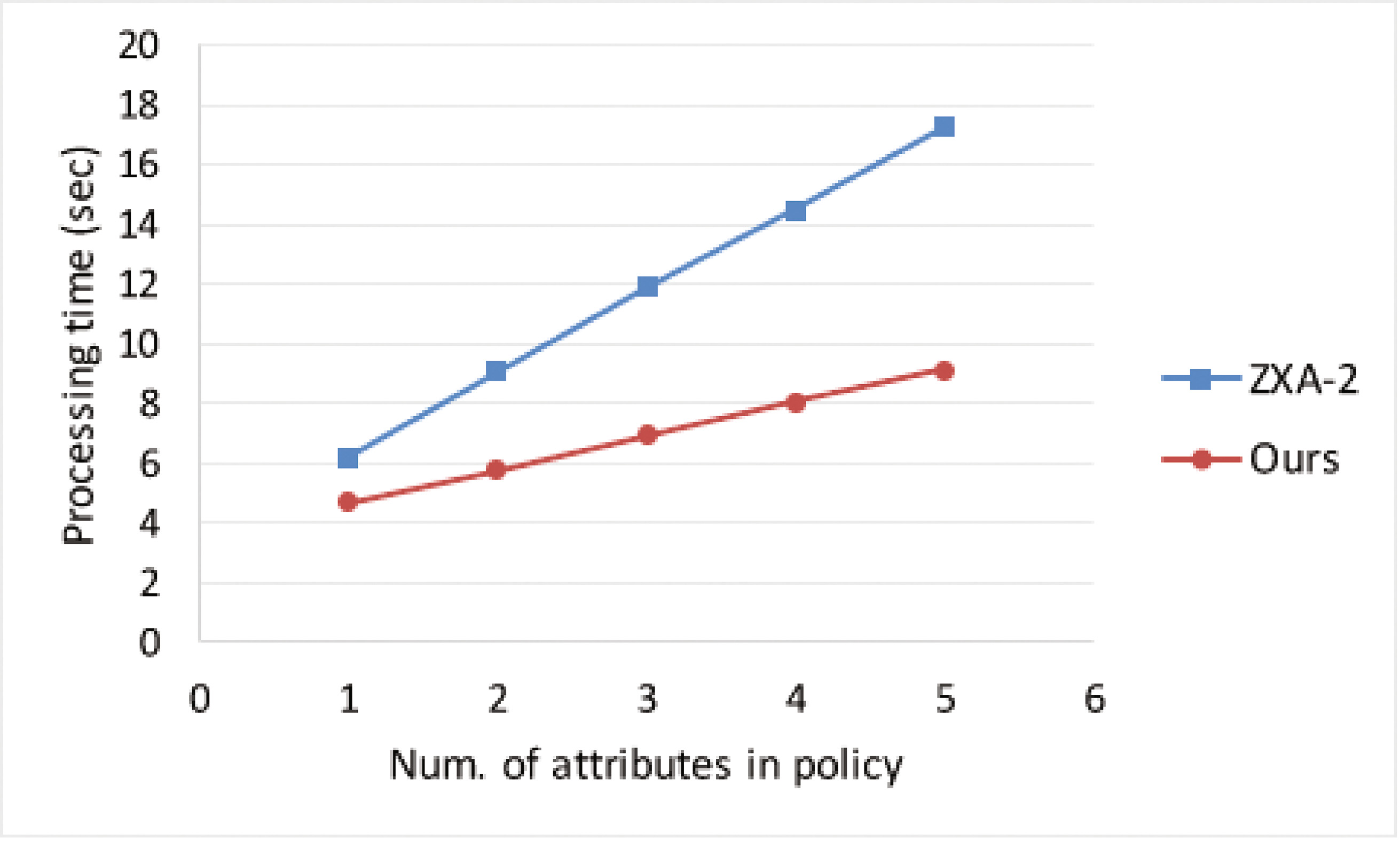
我们在一台具有以下规格的个人计算机上实现了我们的方案和ZXA‐2的索引生成算法：中央处理器：英特尔酷睿 i7‐4790 (3.60 GHz)，内存：8GB，操作系统：CentOS 7.2，浏览器：Firefox 38.3.0。这些算法主要使用 JavaScript编写；配对计算部分用C/C++编写。我们考虑了一个包含13条记录的观看历史，其中包括54个相关关键词（索引）以及数据用户的五个可能的属性。我们测量了索引生成算法的处理时间，取100次试验的平均值。在图3中，横轴表示策略中的属性数量，纵轴表示处理时间（秒）。为简化起见，我们使用仅由与门构成的密文策略。可以看出，我们的方案成本远低于ZXA‐2，且处理时间取决于策略中的属性数量。特别是，对于五个属性，我们的方案耗时约 9秒，而ZXA‐2耗时约18秒。因此，我们的方案显著降低了DOwn的计算开销。

7 结论

我们提出了一种VABKS外包方案，通过将索引生成算法的部分计算外包给云服务器，可显著降低数据所有者的计算开销。该方案支持基于线性秘密共享方案 （LSSS）的表达性强的策略设置，并在随机预言模型下对恶意云服务器是可证明安全的。我们在个人计算机上实现了本方案和先前的VABKS方案的索引生成算法，实验结果表明，本方案的处理时间约为先前方案的一半。本方案基于[18] 中的VABKS通用构造；如何在不依赖通用构造的情况下构建更高效的VABKS 方案仍是一个开放性问题。