死区补偿平均电压补偿和线性补偿法

原创已于 2025-10-02 13:15:15 修改 · 1.3k 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#单片机 #嵌入式硬件

于 2025-10-02 13:14:32 首次发布

电机笔记专栏收录该内容

21 篇文章

订阅专栏

该文章已生成可运行项目，

一、电机死区

下图是六步换相的开关顺序图：S1、S3、S5 我们称为上管，S2、S4、S6 为下管。

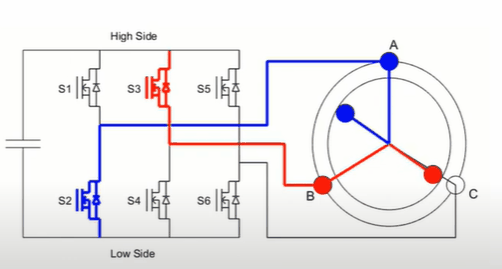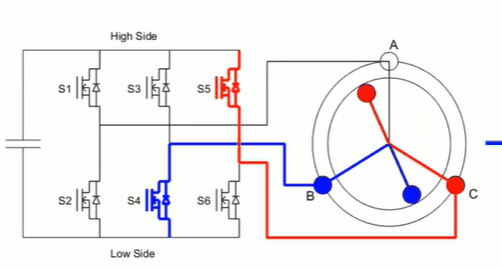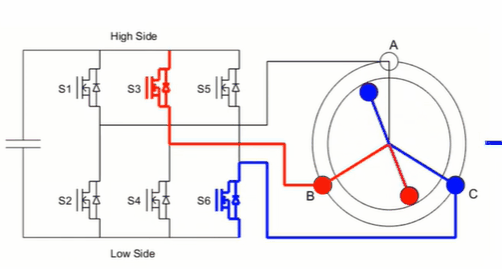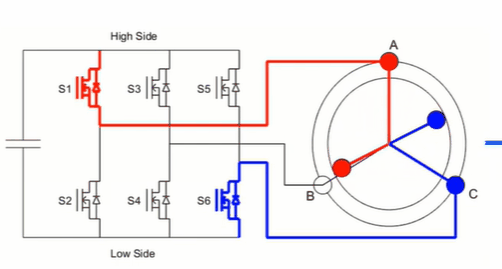
可见，在无刷电机驱动中，不能出现 S1 和 S2、S3 和 S4、S5 和 S6 两两同时导通的情况，因为这样会使电流在上下管之间形成回路，这样并不能驱动电机，还会直接烧毁 MOS。

我们如果要对这六颗 MOS 进行 PWM 驱动，并不需要单独控制六颗，我们只需要配置三个 PWM 输出，然后再由 MCU 生成与之相反的互补的 PWM 即可，其中互补的 PWM 波形保证不会出现上下管同时导通的情况。以S1 和和 S2 波形距离，应该如下图这样：

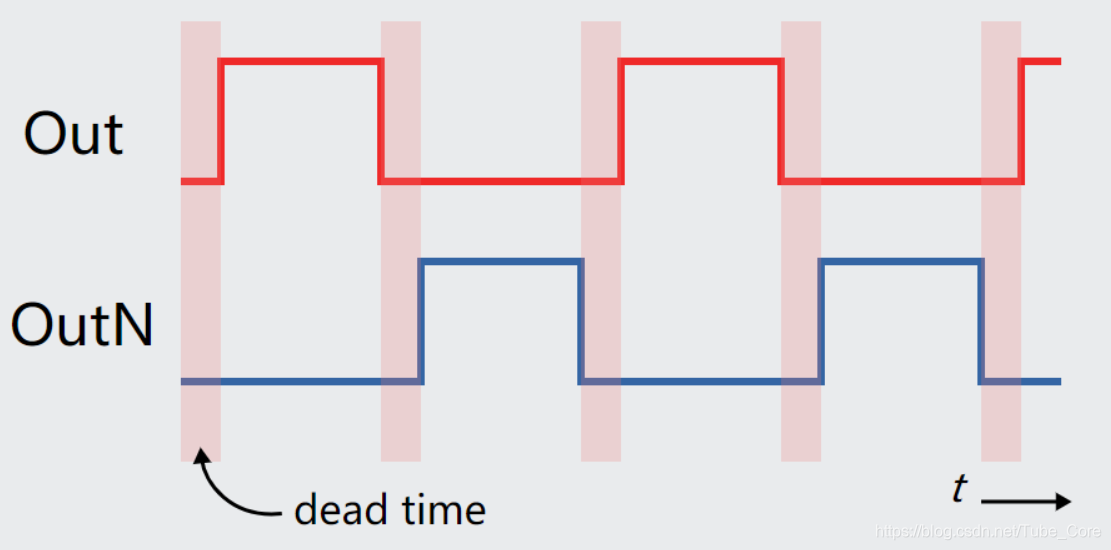
为了确保上下管不会导通，我们往往会再互补波形中设置一个死区时间 (dead time) 留出一些余量。

至此，我们仅需要设置三个 PWM 的周期，占空比，并且配置为互补模式和互补的死区时间，即可完成 MCU 对一个无刷电机的 PWM 外设驱动配置。

二、死区设置后电流波动存在原因

2.1 补偿前后波形对比

在这里截取 TI 的应用笔记截图 (ZHCABA0)，以下是没有死区补偿的相电流，可见在过零点的时候产生了一个类似于台阶的电流波动。

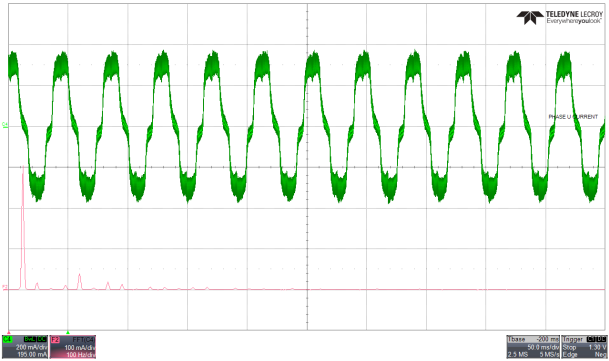
下图则是开启死区补偿时的相电流波形图：

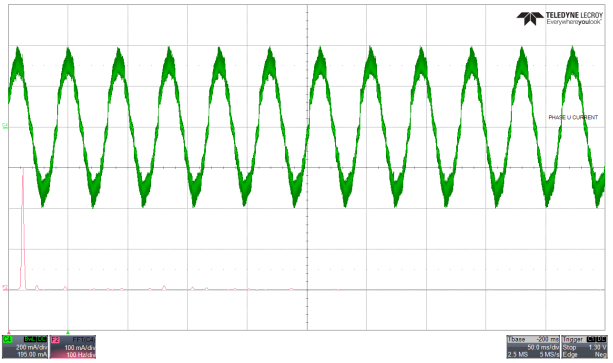
2.2 死区的影响

PWM 插入死区时间，防止上下开关器件同时导通损坏器件，也会引起波动畸变和转矩脉冲，降低系统性能。

影响原因如下：

死区时间越长，逆变器输出基波电压损失越大，电压波形畸变程度越大，堵在基波下降最多，电流波形畸变越严重。
死区时间固定，如果负载功率因数变小，会使一边去输出基波电压幅度增加，电压谐波畸变较小，基波电流幅值减小，电流波形影响率会变大。
当输出电压较低时，空间电压矢量幅值很小，开关器件相对导通时间变短，死区时间影响变大。
死区不仅影响输出电压幅值，还影响相位，使 PWM 波形不再对称于中心，周期空间电压矢量幅值产生偏差，相位也发生变化。

2.3 零电流钳位

在死区时间内，电流由二极管续流，不管电流是什么方向，电流的幅值向零方向减少。如果在死区开始时电流幅值接近于零，则当电流下降到零以后，由于二极管承受不了反电压，阻止了电流的反向流动，在剩余死区时间内，电流将保持位零。

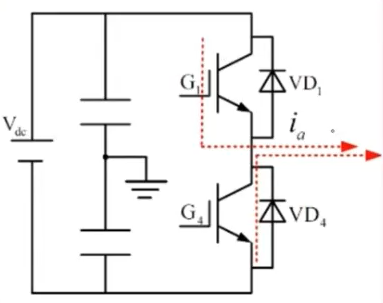
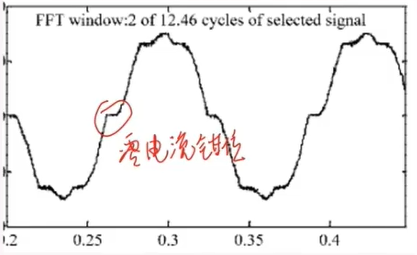
如下图所示，

大电流时 (远离零点)
电流方向明确，不管死区多长，电流都会坚定地走某一边的二极管 → 桥臂电压只产生一个恒定的偏移 (可以通过补偿修正)。

小电流时 (零点附近)

电流方向不稳定，可能随时正负切换，甚至瞬间为零。在死区的空档期，控制器想让上管导通，但电流可能还没换向过来 → 结果二极管继续钳住电压。如果电流方向正好要反向，而桥臂两边的二极管都不情愿导通，就会出现短暂的悬空或错误钳位。

三、死区补偿方法

3.1 平均电压补偿法

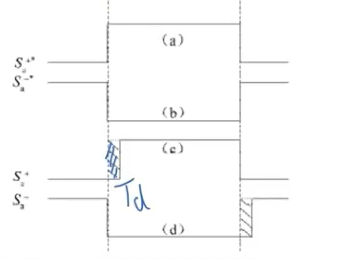
上图是虚线部分是电机死区时间，由此可得出一个周期内的平均死区导致的误差电压为：

$\Delta U_{err}=\frac{T_{d}}{T_{s}}\cdot V_{dc}$

$\Delta U_{err}$ = 因为死区导致的误差电压
$T_{d}$ = 死区时间 (Dead-time)
$T_{s}$ = 周期时间
$V_{dc}$ = 母线电压

如果我们把 mos 的开关管时间也计算进去后可得误差电压：

$\Delta U = \frac{T_d + T_{\text{off}} - T_{\text{on}}}{T_s} \cdot V_{dc}$

$T_{d}$ = 死区时间 (Dead-time)
$T_{on}$ = 开管所需的时间
$T_{\text{off}}$ = 关管所需的时间
$T_{s}$ = 整个 PWM 周期
$V_{dc}$ = 直流母线电压
$\Delta U$ = 调制后的电压

我们将 $T_d + T_{\text{off}} - T_{\text{on}}$ 带入到三项当中，得到 $T_{abc}$ ，再将其带入到三相补偿公式中。

最终我们的三项补偿电压公式可得：

$\begin{array}{l} \Delta U_{a}=\frac{V_{d c}T_{c}}{T_{s}}\cdot\frac{2\operatorname{sign}\left(i_{a}\right)-\operatorname{sign}\left(i_{b}\right)-\operatorname{sign}\left(i_{c}\right)}{3}\\ \Delta U_{b}=\frac{V_{d c}T_{c}}{T_{s}}\cdot\frac{2\operatorname{sign}\left(i_{b}\right)-\operatorname{sign}\left(i_{a}\right)-\operatorname{sign}\left(i_{c}\right)}{3}\\ \Delta U_{c}=\frac{V_{d c}T_{c}}{T_{s}}\cdot\frac{2\operatorname{sign}\left(i_{c}\right)-\operatorname{sign}\left(i_{a}\right)-\operatorname{sign}\left(i_{b}\right)}{3} \end{array}$

$T_{s}$ = 整个 PWM 周期
$T_{c}$ = 死区时间
$V_{dc}$ = 直流母线电压
$\Delta U_{abc}$ = 补偿电压

其中 $sign(x)$ 函数定义如下：

$\operatorname{sign}(x) = \begin{cases} +1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{cases}$

在上面公式当中：

$\frac{2\operatorname{sign}\left(i_{a}\right)-\operatorname{sign}\left(i_{b}\right)-\operatorname{sign}\left(i_{c}\right)}{3}\\$

这一部分是为了确定补偿电流方向，其中电流方向示意如下图：

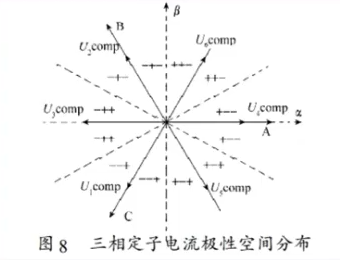
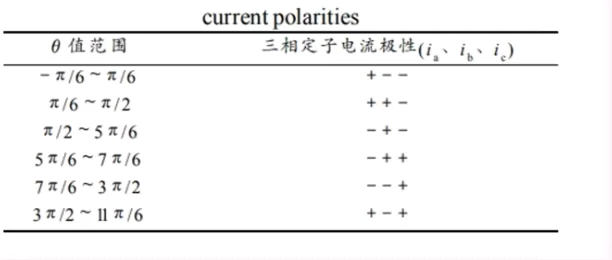
死区使得逆变器输出电压平均值偏小/偏大。偏差的正负取决于电流方向 (由 $sign(x)$ 决定)。所以，补偿就是：按照电流方向，把一个与死区成比例的电压加到参考电压上，从而抵消误差。

也就是：

$i_{abc}$ > 0 → 电流从逆变器流向电机 → 上管导通为主。
$i_{abc}$ < 0 → 电流从电机回灌逆变器 → 下管导通为主。

代码演示：

#include <math.h>

// 输入参数
float Udc;          // 母线电压 (V)
float Ts;           // PWM周期 (s)
float Td;           // 死区时间 (s)
float Ia, Ib, Ic;   // 三相电流 (A)
float Ualpha_ref, Ubeta_ref;  // 原始调制电压 (αβ坐标)

// 输出参数
float Ualpha_cmd, Ubeta_cmd;  // 补偿后的调制电压 (αβ坐标)

// 符号函数
static inline float sign(float x)
{
    if (x > 0.0f) return  1.0f;
    if (x < 0.0f) return -1.0f;
    return 0.0f;
}

void DeadTime_AvgVoltComp(void)
{
    // ==========================
    // 1. 计算电压补偿量 (abc)
    // ==========================
    float Uerr_a = (Td / Ts) * Udc * sign(Ia);
    float Uerr_b = (Td / Ts) * Udc * sign(Ib);
    float Uerr_c = (Td / Ts) * Udc * sign(Ic);

    // ==========================
    // 2. Clarke变换到 αβ坐标
    // ==========================
    float Uerr_alpha = (2.0f/3.0f) * (Uerr_a - 0.5f*Uerr_b - 0.5f*Uerr_c);
    float Uerr_beta  = (2.0f/3.0f) * ((sqrtf(3.0f)/2.0f) * (Uerr_b - Uerr_c));

    // ==========================
    // 3. 在 αβ 坐标上补偿
    // ==========================
    Ualpha_cmd = Ualpha_ref + Uerr_alpha;
    Ubeta_cmd  = Ubeta_ref  + Uerr_beta;
}

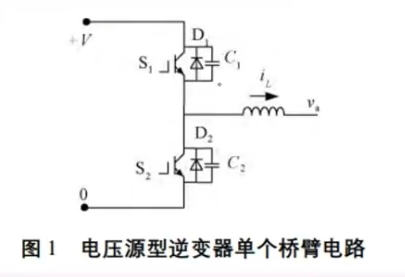
3.2 线性补偿法

平均电压补偿法的补偿波形实际上是方波，因为补偿量受到 $sign(x)$ 影响。以上计算方式仅考虑了 $D_{1}$ 和 $D_{2}$ 反向二极管，然而在实际情况下我们也需要考虑到 $C_{1}$ 和 $C_{2}$ 电容充放过程，所以我们抛弃平均补偿法这种方波补偿，从而使用梯形电压补偿即可解决。

其与平均电压补偿法的区别就是，不再使用 $sign(x)$ 函数，而是使用：

$\Delta U = K_{\mathrm{dead}} \cdot \frac{i_{\mathrm{phase}}}{I_{\mathrm{scale}}}$

$\Delta U$ = 死区补偿电压
$K_{dead}$ = 死区补偿增益（标定参数）
$i_{\text{phase}}$ = 相电流
$I_{scale}$ = 电流缩放系数

线性补偿的波形如下：

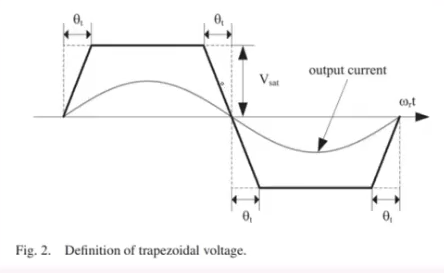
代码如下：

#include <math.h>

// ===================== 参数定义 =====================
#define VDC      24.0f       // 母线电压 (V)
#define Ts       1e-4f       // PWM周期 (s)
#define Td       2e-6f       // 死区时间 (s)
#define Kdead    (VDC * Td / Ts)   // 死区补偿基准系数

// ===================== 输入量 =====================
// 三相电流 (A)，来自ADC采样
float ia, ib, ic;

// αβ电压 (控制器计算得到的期望值)
float Ualpha_ref, Ubeta_ref;

// ===================== 输出量 =====================
float Ualpha_cmd, Ubeta_cmd;  // 补偿后的电压指令

// ===================== 死区补偿函数 =====================
static inline float deadtime_comp(float i_phase)
{
    // 线性补偿：电流越大，补偿越大
    // 正负方向决定补偿符号
    return Kdead * (i_phase / 10.0f); 
    // 分母 10.0f 只是一个缩放，避免补偿过大，需要标定
}

void DeadTime_Comp_Linear(void)
{
    // 计算三相补偿电压
    float Ua_comp = deadtime_comp(ia);
    float Ub_comp = deadtime_comp(ib);
    float Uc_comp = deadtime_comp(ic);

    // Clarke 变换，把补偿量投到 αβ 坐标系
    float Ualpha_comp = (2.0f/3.0f) * (Ua_comp - 0.5f*Ub_comp - 0.5f*Uc_comp);
    float Ubeta_comp  = (2.0f/3.0f) * ((sqrtf(3)/2.0f) * (Ub_comp - Uc_comp));

    // 补偿到电压指令
    Ualpha_cmd = Ualpha_ref + Ualpha_comp;
    Ubeta_cmd  = Ubeta_ref  + Ubeta_comp;
}

本文章已经生成可运行项目