滑模控制与电机角度滑模观测器解析

原创已于 2025-09-24 11:17:59 修改 · 1k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #嵌入式硬件 #单片机 #自动化

于 2025-09-24 11:16:37 首次发布

电机笔记专栏收录该内容

20 篇文章

订阅专栏

一、滑模控制

1.1 滑模控制器概述

滑模控制是一种非线性控制方法。它的核心思想是：在状态空间中设计一个滑模面 (sliding surface)，比如：

$s(x)=0$

$s(x)$ = 状态的某种组合 (比如速度误差、电流误差)

如果 $s(x)$ 是速度误差函数，所谓滑模面也就是速度误差等于 0 的情况。通过控制律让系统快速到达这个面，以速度误差举例，就是让其误差快速到达 0。一旦到达滑模面，系统就沿着这个面移动，最终达到收敛状态。

换种通俗的例子：给系统设计一条轨道 (滑模面)，不管它一开始在哪，控制器都会强行把它推到轨道上，并且保证它沿轨道滑到终点。

1.2 滑模控制举例

1.2.1 滑模控制调速案例引入

我们考虑一个直流电机调速的场景，用滑模控制给直流电机调速。

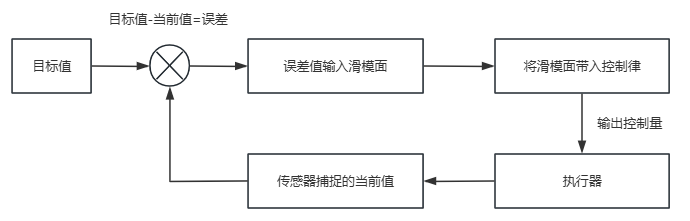
其流程是

定义误差 (目标速度减去当前速度)
将误差输入滑模面 (将误差求积分，但是滑模函数的目标值 = 0)
滑模面输入控制律，控制律输出调速电压。
捕捉当前速度，计算误差。

1.2.2 定义误差

$error=\omega ^{*}-\omega$

$\omega ^{*}$ = 目标速度
$\omega$ = 实际速度

1.2.3 设计滑模面函数 $s(x)$

$s = error + \lambda \int error \, dt$

$\lambda$ = 积分权重

其滑模函数 $s(x)$ = 0，也就是相当于我们的理想情况下应该是 0 误差的。

1.2.4 控制律

$u=u_{eq}-K\cdot sgn(s)$

$u=$ 实际施加到系统上的控制输入 (在这里是电压)
$u_{eq}$ = 等效控制电压 (在这里可以是通过电机的 KV 计算的电压)
$K$ = 滑模增益系数
$sgn(s)$ = 符号函数，内的 s 就是我们的滑模面函数

其中 $sgn(s)$ 函数定义如下：

$\operatorname{sgn}(x) = \begin{cases} +1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{cases}$

其中这个等效控制电压 $u_{eq}$ 相当于是在理想情况，无外部干扰的对应关系。比如使用电机的 KV 值直接算出来的速度。但是通常来说电机不仅会带载，还会发热，这些都会影响到 KV 值的参数。其控制律就是利用这个值和误差累加做差得到的。我们的等效控制值越准，整个系统的性能就越好。

1.2.5 离散化后代码演示

下面代码是滑模控制器控制电机速度的代码：

// 参数
float lambda = 50.0f;    // λ 系数
float Ts = 0.001f;       // 采样周期 (1 kHz)
float K = 2.0f;          // 切换增益
float Kv = 1000.0f;      // 电机常数 [rpm/V]，需要根据电机实际参数修改

// 变量
float e;                 // 误差
float e_int = 0.0f;      // 误差积分
float s;                 // 滑模面
float u;                 // 控制输入（电压命令）

// 滑模控制函数
float sliding_mode_control(float ref_speed, float meas_speed)
{
    // 计算误差
    e = ref_speed - meas_speed;

    // 误差积分 (离散积分)
    e_int += e * Ts;

    // 滑模面公式 s = e + λ ∫ e dt
    s = e + lambda * e_int;

    // 等效控制：补偿反电动势 (简单模型)
    // Kv [rpm/V] -> 转速除以 Kv 得到所需电压
    float u_eq = meas_speed / Kv;

    // 切换控制项
    float u_sw = -K * (s > 0 ? 1.0f : -1.0f);

    // 总控制律
    u = u_eq + u_sw;

    return u;  // 输出电机电压命令
}

1.3 滑模切换面和滑模运动过程图解

1.3.1 滑模切换面

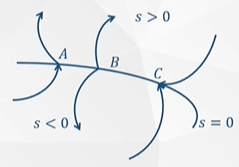
这张图是滑模控制 (Sliding Mode Control,SMC) 里面常见的切换面 (Switching Surface) 上三种典型点的特性示意图。

含义如下：

横线 (s = 0)：表示切换面 (switching surface)。
s>0、s<0：表示系统状态在切换面两侧的区域。
A、B、C 三个点：表示系统轨迹与切换面相交或接触时可能的三种情况。

A 点 (穿越点)：

系统状态从 s<0 一侧穿到 s>0 一侧。说明滑模控制律设计得不好，轨迹没有被吸引到切换面，而是直接穿过去。不会形成滑模运动。

B 点 (驻留点 / 临界点)：

系统状态到达切换面时，切换面的法向速度分量为 0。表示轨迹在切换面上既不进入也不离开，可能停在边界上。稍微扰动就会跑到一边去，不稳定。

C 点 (到达点 / 吸引点)：

系统状态到达切换面，并被两侧的控制力推向切换面。说明系统设计合理，轨迹最终会被“吸附”在切换面上，形成稳定的滑模运动 (Sliding motion)。这是滑模控制希望达到的状态。

1.3.2 滑模运动过程

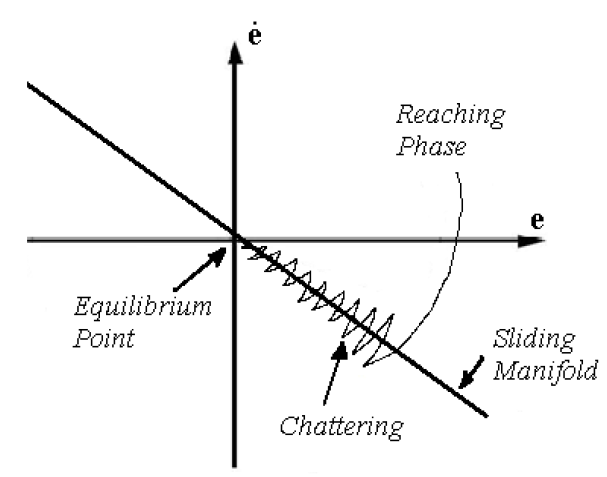
这个图也是 滑模控制（Sliding Mode Control, SMC） 的典型示意图，展示的是系统状态轨迹在切换面上的运动情况。

滑模面的横纵分别是误差和和归零的导数，也就是误差和误差变化率。误差越大，变化率就越大，在滑模面这种理想情况下是呈线性关系的，但是我们控制的线回归零点却是曲线，一定要梳理好这张图的关系！！！

坐标轴：

横轴 (位置/误差)
纵轴 (速度/误差导数)

直线 $s=0$ :

切换面，也叫滑模面。它是设计出来的，使得当轨迹被吸引到这条线上后，系统误差可以稳定收敛。

曲折的轨迹：

系统状态 $(x_{1},x_{2})$ 由初始点开始，受控制律作用逐渐靠近并贴合在切换面 $s=0$ 上。

$\dot{x}$ 箭头方向：

表示在切换面上系统状态沿着轨迹向原点 (平衡点) 运动。

Reaching Phase（到达阶段）

系统状态最开始不在滑模面上。控制律会驱动它逐渐靠近滑模面。

Sliding Mode（滑动阶段）

状态一旦进入滑模面（黑线）附近，就被“粘住”，沿着黑线往原点移动。这就是滑模。

Chattering（抖振）

由于控制输入的开关特性，系统不会严格落在黑线上，而是会在黑线附近高频抖动。这就是图上画的锯齿波。

Equilibrium Point（平衡点）

当状态最终滑到原点时，意味着误差 $e=0,\dot{e}=0$ 。这就是目标状态 (比如速度完全跟随指令)。

1.4 与 PID 控制的区别

我们可见，PID 控制和非常相似，都有累加积分误差然后输出。

其最大的区别是滑模控制是非线性控制，而 PID 线性控制。其次的区别是，滑模控制的控制律依赖等效控制这个变量，而 PID 在任何地方也不依赖等效控制。

1.4.1 线性控制与非线性控制

对于 PID 和滑模控制来说，线性和非线性的区别是对于输出的区别：

$u(t) = K_p e(t) + K_i \int_0^t e(\tau) \, d\tau + K_d \frac{de(t)}{dt}$

其中比例项、积分项、微分项均有线性依赖关系。

我们再看滑模控制的控制律：

$u=u_{eq}-K\cdot sgn(s)$

其在 $sgn(s)$ 函数的作用下产生跳变：当 $s>0$ 输出 $-K$ ，当 $s<0$ 输出 $+K$ 所以这里的 $sgn(s)$ 是典型非线性函数。

二、滑模观测器基本概念

2.1 什么是观测器

观测器观测的是传感器无法测量的变量。顾名思义是为了观测某个变量，但是这个变量我又没有传感器可以直接测量，比如经典的一个例子：

火箭发动机的温度，温度非常高，不可能有传感器直接测量的，那么这时候就要用观测器，我虽然不能直接测火箭发动机温度，但是我可以测量火箭表面温度，然后通过热传导公式计算出发动机温度。

假设火箭温度关系满足下列公式：

$T_{surface}=m\cdot u+n\cdot T_{engine}$

$T_{surface}$ = 火箭表面温度
$u$ = 燃料量
$m$ = 不定系数
$n$ = 不定系数
$T_{engine}$ = 发动机温度

其中 $u$ 是燃料量， $m$ 、 $n$ 是不确定系数。

实际测得的表面温度 $T_{surface}$ 与模型计算得到的温度 $T_{engine}$ 一般不相等。为此，我们设计一个状态观测器，使 $T_{engine}$ 逐渐逼近 $T_{surface}$ ，并在这个过程中动态修正系数 $m$ 、 $n$ 从而实时估计发动机温度。

2.2 滑膜观测器基本概念

滑模观测器 (Sliding Mode Observer，SMO）是一种用于系统状态估计的非线性观测器，尤其常用于电机控制 (如无传感器控制的永磁同步电机 PMSM) 来估计难以直接测量的量，比如转子位置、速度或反电动势。

滑模观测器是一类基于滑模控制思想的观测器，滑模观测器也包括滑模控制最核心的滑模面和控制律思想。

三、应用观测电机角度的滑模观测器

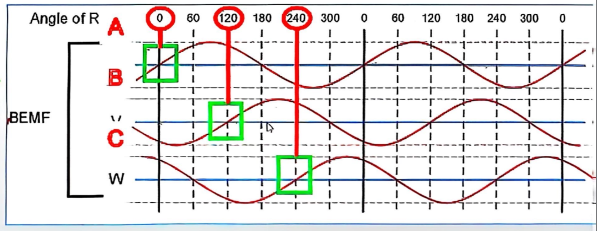
3.1 反电动势与角度的关系

由于电机三相角度相差为 120° ，A 相的反电动势，相位差为0°；B 相则是120°；C 相是240°

也就是三项反电动势公式为：

$V_{BEMF_A} = \omega \times k_{e}\times sin(\theta + 0 )$

$V_{BEMF_B} = \omega \times k_{e}\times sin(\theta + 120 )$

$V_{BEMF_C} = \omega \times k_{e}\times sin(\theta + 240 )$

下图则是三项反电动势和角度的关系。可见，我们只要能准确的获得当前电机的反电动势，即可计算器的当前角度。

3.2 静态电压方程

3.2.1 A、B、C 三相电压方程

这是一个三相无刷电机（或者同步电机）的 等效电路模型，是相电路（单相绕组）建模之后，再按三相星形（Y 形）连接表示出来的。

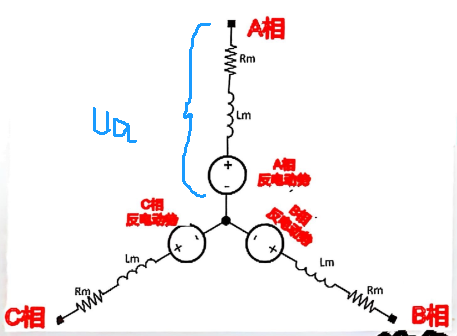
我们将 A 相单独列出来，如下图：

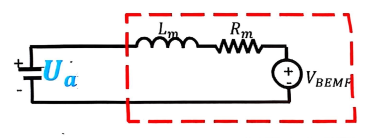
可见，对电压有阻碍作用的有：

$R_{m}$ = 相电阻（绕组电阻）
$L_{m}$ = 相电感（绕组电感）
$V_{BEMF}$ ：反电动势源，用来表示转子旋转时感应出来的电压。

整理公式可得：

$\left\{\begin{matrix} U_a = R_m i_a + L_m \frac{di_a}{dt} + e_a \\ U_b = R_m i_b + L_m \frac{di_b}{dt} + e_b \\ U_c = R_m i_c + L_m \frac{di_c}{dt} + e_c \end{matrix}\right.$

$U_{abc}$ = 三相绕组的端电压 (A、B、C)。这是逆变器通过 PWM 作用在定子绕组上的电压
$i_{abc}$ = 三相绕组的电流 (A、B、C)
$R_{m}$ = 定子相电阻 (每一相绕组的电阻)
$L_{m}$ = 定子相电感 (假设三相对称，电感相同，不考虑互感时的简化模型)
$\frac{di_{abc}}{dt}$ = 三相电流对时间的导数，对应绕组电感电压降。
$e_{abc}$ = 三相反电动势 (Back-EMF)，由转子磁场切割定子绕组磁链产生。它们与转速、转子位置及磁链相关。

3.2.1 α、β 轴电压方程

在 α、β 轴的电压方程和三项电压方程一样：

$\left\{\begin{matrix} U_\alpha = R_m i_\alpha + L_m \frac{d i_\alpha}{dt} + e_\alpha \\ U_\beta = R_m i_\beta + L_m \frac{d i_\beta }{dt} + e_\beta \end{matrix}\right.$

$U_{\alpha \beta }$ = 三相绕组的端电压 (α、β)。这是逆变器通过 PWM 作用在定子绕组上的电压
$i_{\alpha \beta}$ = 三相绕组的电流 (α、β)
$R_{m}$ = 定子相电阻 (每一相绕组的电阻)
$L_{m}$ = 定子相电感 (假设三相对称，电感相同，不考虑互感时的简化模型)
$\frac{di_{\alpha \beta}}{dt}$ = 三相电流对时间的导数，对应绕组电感电压降。
$e_{\alpha \beta}$ = 三相反电动势 (Back-EMF)，由转子磁场切割定子绕组磁链产生。它们与转速、转子位置及磁链相关。

将其变形的可得：

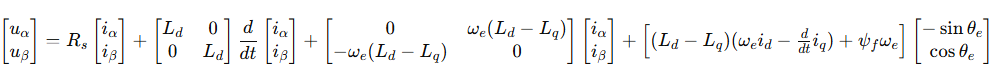
$u_{\alpha \beta }$ = 定子在 $\alpha \beta$ 静止坐标系下的电压分量
$i_{\alpha \beta }$ = 定子在 $\alpha \beta$ 静止坐标系下的电流分量
$i_{dq}$ = 定子电流在 $dq$ 旋转坐标系下的分量 (d 轴、q 轴)
$L_{dq}$ = $dq$ 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$R_{s}$ = 定子电阻
$\psi _{f}$ = 由永磁体产生的磁链 (主磁链)
$\theta$ = 转子电角度 (电角位置，dq 坐标旋转角度)
$\omega _{e}$ = 电角速度

我们来一步一步分析这个公式：

定子电阻压降：

$R_{s} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix}$

$R_{s}$ = 定子电阻
$i_{\alpha \beta }$ = 定子在 $\alpha \beta$ 静止坐标系下的电流分量

电感和交叉耦合项：

加号前是电感的压降；加号后是由于电机是转子坐标变化，d、q 轴电感不相等时 (凸极电机)，会出现耦合效应：

$\begin{bmatrix} L_{d} & 0 \\ 0 & L_{d} \end{bmatrix} \frac{d}{dt} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} + \begin{bmatrix} 0 & \omega_{e}(L_{d}-L_{q}) \\ -\omega_{e}(L_{d}-L_{q}) & 0 \end{bmatrix} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix}$

$L_{dq}$ = d、q 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$i_{\alpha \beta }$ = 定子在 α、β 轴静止坐标系下的电流分量
$\omega _{e}$ = 电角速度

如果是 d、q 相等的表贴式电机则只有加号前的部分：

$\begin{bmatrix} L_{d} & 0 \\ 0 & L_{d} \end{bmatrix} \frac{d}{dt} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix}$

$L_{dq}$ = d、q 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$i_{\alpha \beta }$ = 定子在 α、β 轴静止坐标系下的电流分量

转子磁链相关项：

由永磁体产生的反电动势导致的压降，这个我们在下面的公式直接写成 $E_{\alpha \beta }$

$\Big[ (L_{d}-L_{q})\big(\omega_{e} i_{d} - \tfrac{d}{dt} i_{q}\big) + \psi_{f}\omega_{e} \Big]\begin{bmatrix} -\sin\theta_{e} \\ \cos\theta_{e} \end{bmatrix}=\begin{bmatrix} E_{\alpha } \\ E_{\beta } \end{bmatrix}$

$L_{dq}$ = $dq$ 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$\omega _{e}$ = 电角速度
$i_{dq}$ = 定子电流在 $dq$ 旋转坐标系下的分量 (d 轴、q 轴)
$\psi _{f}$ = 由永磁体产生的磁链 (主磁链)
$\theta$ = 转子电角度 (电角位置，d、q 坐标旋转角度)
$E_{\alpha \beta }$ = α、β 轴的反电动势

3.2.2 α、β 轴电压方程改成写电流微分形式

$\frac{d}{dt}\begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix}= \begin{bmatrix} -\tfrac{R_s}{L_d} & -\tfrac{\omega_e (L_d - L_q)}{L_d} \\ \tfrac{\omega_e (L_d - L_q)}{L_d} & -\tfrac{R_s}{L_d} \end{bmatrix} \begin{bmatrix} i_{\alpha} \\ i_{\beta} \end{bmatrix} +\frac{1}{L_d} \begin{bmatrix} u_{\alpha} \\ u_{\beta} \end{bmatrix} -\frac{1}{L_d} \begin{bmatrix} E_{\alpha} \\ E_{\beta} \end{bmatrix}$

$u_{\alpha \beta }$ = 定子在 α、β 轴静止坐标系下的电压分量
$i_{\alpha \beta }$ = 定子在 α、β 轴静止坐标系下的电流分量
$i_{dq}$ = 定子电流在 d、q 旋转坐标系下的分量 (d 轴、q 轴)
$L_{dq}$ = d、q 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$R_{s}$ = 定子电阻
$\psi _{f}$ = 由永磁体产生的磁链 (主磁链)
$\theta$ = 转子电角度 (电角位置，d、q 坐标旋转角度)
$\omega _{e}$ = 电角速度
$E_{\alpha \beta }$ = α、β 轴的反电动势

3.3 反电动势的滑模观测器

反电动势的滑模观测器核心思想是，根据电流和预估电流的误差预估一个反电动势 $v_{\alpha \beta }$ ，然后带入电流微分公式，得到预估电流。循环这个过程，我们便得到了 α、β 轴的反电动势。

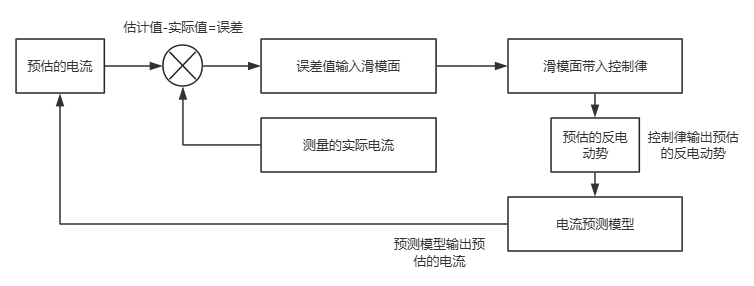
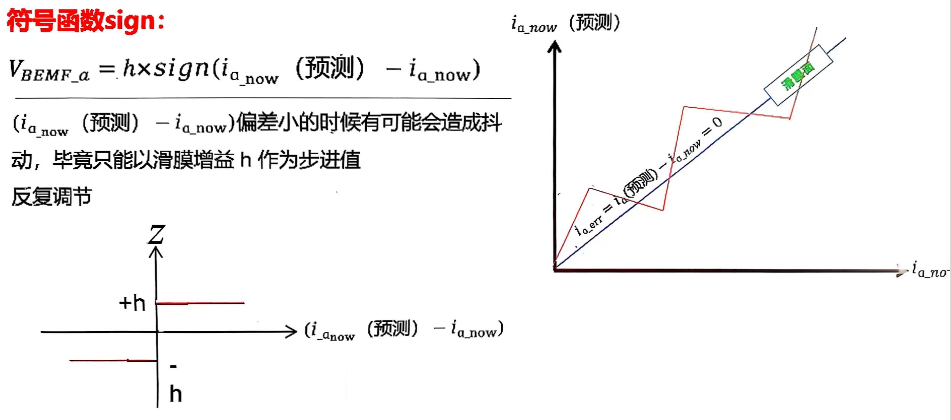
3.3.1 构造反电动势的滑模观测面 $s(x)$

$s=\left[\begin{array}{l} s_{1} \\ s_{2} \end{array}\right]=\left[\begin{array}{l} \tilde{i}_{\alpha} \\ \tilde{i}_{\beta} \end{array}\right]=\left[\begin{array}{l} \hat{i}_{\alpha}-i_{\alpha} \\ \hat{i}_{\beta}-i_{\beta} \end{array}\right]$

$\tilde{i}_{\alpha\beta }$ = 电流估计误差
$\hat{i}_{\alpha\beta }$ = 电流估计值

此时，在 $s(x) = 0$ 意味着我们观测的反电动势是正确的。

3.3.2 构造反电动势的控制律

$\left[ \begin{array}{l} v_{\alpha} \\ v_{\beta} \end{array} \right] = \left[ \begin{array}{l} h \cdot \operatorname{sign}\left(\hat{i}_{\alpha}-i_{\alpha}\right) \\ h \cdot \operatorname{sign}\left(\hat{i}_{\beta}-i_{\beta}\right) \end{array} \right]$

其中 $sgn(s)$ 函数定义如下：

$\operatorname{sign}(x) = \begin{cases} +1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{cases}$

此时我们便得到了预估的 α 和 β 轴的反电动势。

其效果是这样的，那条 45° 直线是滑模面。横轴是误差，纵轴是误差的导数。

在理想的情况下，也就是滑模面，也就是误差和误差回正导数正线性比例。

3.3.3 电流微分公式 (电流预估模型)

$\frac{d}{d t} \begin{bmatrix} \hat{i}_{\alpha} \\ \hat{i}_{\beta} \end{bmatrix} = \begin{bmatrix} -\frac{R_{s}}{L_{d}} & -\frac{\omega_{e}(L_{d}-L_{q})}{L_{d}} \\ \frac{\omega_{e}(L_{d}-L_{q})}{L_{d}} & -\frac{R_{s}}{L_{d}} \end{bmatrix} \begin{bmatrix} \hat{i}_{\alpha} \\ \hat{i}_{\beta} \end{bmatrix} + \frac{1}{L_{d}} \begin{bmatrix} u_{\alpha} \\ u_{\beta} \end{bmatrix} - \frac{1}{L_{d}} \begin{bmatrix} v_{\alpha} \\ v_{\beta} \end{bmatrix} \quad$

$\hat{i}_{\alpha\beta }$ = 电流估计值
$v_{\alpha \beta }$ = 估计的反电动势
$u_{\alpha \beta }$ = 定子在 α、β 轴静止坐标系下的电压分量
$i_{dq}$ = 定子电流在 d、q 旋转坐标系下的分量 (d 轴、q 轴)
$L_{dq}$ = d、q 轴电感 (分别是沿磁链方向的电感和垂直于磁链方向的电感)
$R_{s}$ = 定子电阻
$\psi _{f}$ = 由永磁体产生的磁链 (主磁链)
$\theta$ = 转子电角度 (电角位置，d、q 坐标旋转角度)
$\omega _{e}$ = 电角速度

3.3.3 代码演示

void SMO_position_estimate(void) {

    // Clarke 变换：三相电流 -> αβ
    float Ialpha = CS_M0.current_a;
    float Ibeta  = _1_SQRT3 * CS_M0.current_a + _2_SQRT3 * CS_M0.current_b;

    // 根据电流微分方程构造电流预测模型
    // 核心思想是输入预估的反电动势反推出来电流
    //其中 SMO_Ualpha 和 SMO_Ubeta 是逆变器控制的电压 Ealpha 和 Ebeta 是滑模观测器估计的反电动势
    Est_Ialpha = a_coeff * Est_Ialpha + b_coeff * (SMO_Ualpha - Ealpha);
    Est_Ibeta  = a_coeff * Est_Ibeta  + b_coeff * (SMO_Ubeta  - Ebeta);

    // 电流误差 观测误差与实际误差 也就是滑模面函数
    float Ialpha_Err = Est_Ialpha - Ialpha;
    float Ibeta_Err  = Est_Ibeta  - Ibeta;

    // 构造控制律
    Ealpha = h * sat(Ialpha_Err, 0.5f);
    Ebeta  = h * sat(Ibeta_Err,  0.5f);

    // 低通滤波
    Ealpha_flt = 0.1f * Ealpha_flt + 0.9f * Ealpha;
    Ebeta_flt  = 0.1f * Ebeta_flt  + 0.9f * Ebeta;

    // 反电动势求角度 使用 atan2 函数计算电角度
    SMO_Est_theta = -atan2f(Ealpha_flt, Ebeta_flt);
}

set 函数定义：

float sat(float err, float limits) {
  if (err > limits) return 1;
  else if (err < -limits) return -1;
  else
    return err / limits;
}

3.4 通过 α 和 β 轴反电动势计算角度

因为 α 轴和 β 轴呈 90°，所以使用反正切角度即可推算出电角度。

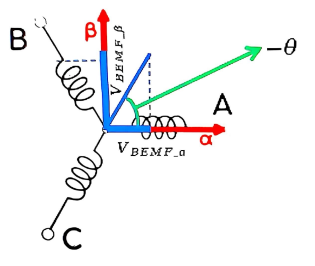
也就是：

$\theta =\arctan (\frac{E_{\alpha }}{E_{\beta }})$

$\theta$ = 转子电角度 (电角位置，d、q 坐标旋转角度)
$E_{\alpha \beta }$ = α、β 轴的反电动势

对应上面代码的：

// 反电动势求角度 使用 atan2 函数计算电角度
    SMO_Est_theta = -atan2f(Ealpha_flt, Ebeta_flt);