✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
在当今数字化时代,无线通信技术的发展日新月异。无论是移动通信、物联网还是工业自动化,都离不开高效可靠的无线网络。然而,随着用户数量的快速增长和通信设备的多样化,网络的规模和复杂性也在不断增加。因此,研究和优化网络性能变得尤为重要。
在无线通信中,误码率是衡量信号传输质量的重要指标。对于上行用户而言,误码率直接影响到数据传输的可靠性和速度。因此,了解和优化上行用户的平均误码率是提高网络性能的关键。
本文将探讨生成不同网络规模和不同集中式检测方法下的上行用户平均误码率的问题。首先,我们将介绍网络规模和集中式检测方法的概念,然后分析它们对上行用户平均误码率的影响。
网络规模是指网络中的用户数量和设备数量。随着用户数量的增加,网络的复杂性也随之增加。这可能导致信号传输过程中的干扰增加,从而影响上行用户的误码率。因此,在生成不同网络规模下的上行用户平均误码率时,我们需要考虑网络的容量和拥塞情况。
集中式检测方法是一种通过中心节点对上行用户的信号进行检测和处理的方法。这种方法可以提高信号的可靠性和传输速度,从而降低误码率。然而,集中式检测方法可能需要更多的计算资源和传输带宽。因此,在生成不同集中式检测方法下的上行用户平均误码率时,我们需要权衡资源利用和误码率的关系。
为了研究上述问题,我们设计了一系列实验。我们首先搭建了不同规模的网络模型,并模拟了上行用户的数据传输过程。然后,我们使用不同的集中式检测方法对数据进行处理,并记录了上行用户的误码率。最后,我们分析了实验结果,并总结了网络规模和集中式检测方法对上行用户平均误码率的影响。
实验结果表明,网络规模和集中式检测方法对上行用户平均误码率有着显著影响。随着网络规模的增加,上行用户的误码率呈现出逐渐增加的趋势。这是由于网络容量的限制和拥塞情况的加剧导致信号传输的干扰增加。另一方面,采用不同的集中式检测方法可以显著降低上行用户的误码率。然而,不同的方法在资源利用和误码率之间存在着权衡关系。
综上所述,生成不同网络规模和不同集中式检测方法下的上行用户平均误码率是一个复杂而重要的问题。通过研究和优化网络规模、集中式检测方法以及资源利用的关系,我们可以提高上行用户的数据传输可靠性和速度。这对于实现高效可靠的无线通信网络至关重要,也对于推动数字化时代的发展具有重要意义。
📣 部分代码
function R = functionRlocalscattering(M,theta,ASDdeg,antennaSpacing,distribution)%Generate the spatial correlation matrix for the local scattering model,%defined in (2.23) for different angular distributions.%%INPUT:%M = Number of antennas%theta = Nominal angle%ASDdeg = Angular standard deviation around the nominal angle% (measured in degrees)%antennaSpacing = (Optional) Spacing between antennas (in wavelengths)%distribution = (Optional) Choose between 'Gaussian', 'Uniform', and% 'Laplace' angular distribution. Gaussian is default%%OUTPUT:%R = M x M spatial correlation matrix%%%This Matlab function was developed to generate simulation results to:%%Emil Bjornson, Jakob Hoydis and Luca Sanguinetti (2017),%"Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency",%Foundations and Trends in Signal Processing: Vol. 11, No. 3-4,%pp. 154-655. DOI: 10.1561/2000000093.%%For further information, visit: https://www.massivemimobook.com%%This is version 1.1 (Last edited: 2017-11-16)%%License: This code is licensed under the GPLv2 license. If you in any way%use this code for research that results in publications, please cite our%monograph as described above.%Set the antenna spacing if not specified by inputif nargin < 4%Half a wavelength distanceantennaSpacing = 1/2;end%Set angular distribution to Gaussian if not specified by inputif nargin<5distribution = 'Gaussian';end%Compute the ASD in radians based on inputASD = ASDdeg*pi/180;%The correlation matrix has a Toeplitz structure, so we only need to%compute the first row of the matrixfirstRow = zeros(M,1);%Go through all the columns of the first rowfor column = 1:M%Distance from the first antennadistance = antennaSpacing*(column-1);%For Gaussian angular distributionif strcmp(distribution,'Gaussian')%Define integrand of (2.23)F = @(Delta)exp(1i*2*pi*distance*sin(theta+Delta)).*exp(-Delta.^2/(2*ASD^2))/(sqrt(2*pi)*ASD);%Compute the integral in (2.23) by including 20 standard deviationsfirstRow(column) = integral(F,-20*ASD,20*ASD);%For uniform angular distributionelseif strcmp(distribution,'Uniform')%Set the upper and lower limit of the uniform distributionlimits = sqrt(3)*ASD;%Define integrand of (2.23)F = @(Delta)exp(1i*2*pi*distance*sin(theta+Delta))/(2*limits);%Compute the integral in (2.23) over the entire intervalfirstRow(column) = integral(F,-limits,limits);%For Laplace angular distributionelseif strcmp(distribution,'Laplace')%Set the scale parameter of the Laplace distributionLaplaceScale = ASD/sqrt(2);%Define integrand of (2.23)F = @(Delta)exp(1i*2*pi*distance*sin(theta+Delta)).*exp(-abs(Delta)/LaplaceScale)/(2*LaplaceScale);%Compute the integral in (2.23) by including 20 standard deviationsfirstRow(column) = integral(F,-20*ASD,20*ASD);endend%Compute the spatial correlation matrix by utilizing the Toeplitz structureR = toeplitz(firstRow);
⛳️ 运行结果
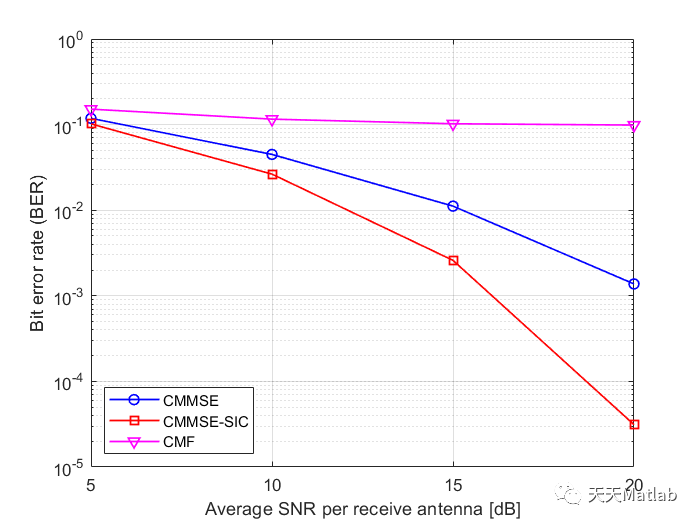
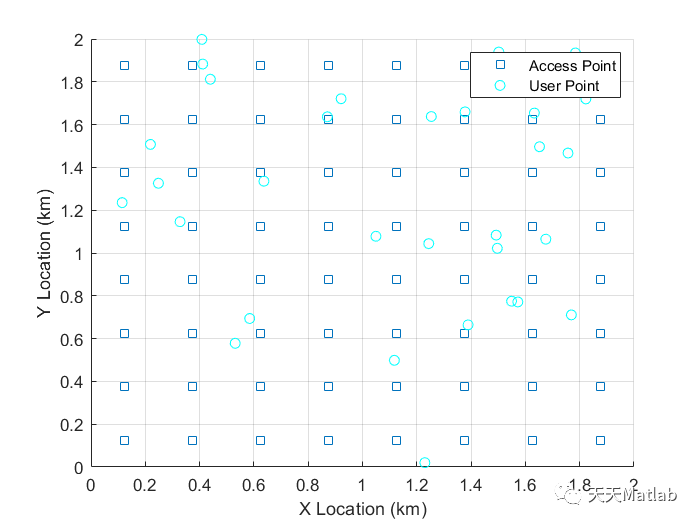
🔗 参考文献
[1] 温杨.基于DFT-SOFDM的上行链路传输技术研究[D].电子科技大学[2023-10-14].DOI:CNKI:CDMD:2.2007.100591.
[2] 赵进平,苑玉龙.CDMA中盲自适应多用户检测算法的研究与分析[J].信阳农业高等专科学校学报, 2010(002):020.
[3] 朱敏.无源光网络及其光子网格应用的关键技术研究[D].上海交通大学[2023-10-14].





 本文探讨了在网络规模扩大和集中式检测方法变化下,上行用户误码率的影响。通过Matlab仿真,研究了用户数量、网络复杂性、信号干扰与资源利用之间的关系,揭示了优化策略对提升通信效率的重要性。
本文探讨了在网络规模扩大和集中式检测方法变化下,上行用户误码率的影响。通过Matlab仿真,研究了用户数量、网络复杂性、信号干扰与资源利用之间的关系,揭示了优化策略对提升通信效率的重要性。

















 1105
1105

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










