✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
多式联运是一种将不同的运输方式(如公路、铁路、航空等)整合起来,以提高运输效率和降低成本的物流管理策略。在现实生活中,多式联运路径优化问题是一个具有挑战性的任务,因为它需要考虑到不同的运输方式、不同的运输网络以及不确定的因素。本篇博文将介绍如何利用帝国企鹅算法、遗传算法和粒子群AFO算法来求解这一问题。
首先,我们来了解一下帝国企鹅算法。帝国企鹅算法是一种模拟帝国企鹅行为的优化算法,它通过模拟帝国企鹅的迁徙行为来搜索最优解。在多式联运路径优化问题中,帝国企鹅算法可以用来搜索最优的路径组合,以最小化总运输成本。算法的基本思想是通过不断迁徙和更新帝国企鹅的位置来寻找更优的解决方案。
接下来,我们介绍遗传算法。遗传算法是一种模拟生物进化过程的优化算法,它通过模拟自然选择、交叉和变异等操作来搜索最优解。在多式联运路径优化问题中,遗传算法可以用来生成和优化路径的组合,以最小化总运输时间。算法的基本思想是通过不断迭代和选择最优个体来逐步优化解决方案。
最后,我们介绍粒子群AFO算法。粒子群AFO算法是一种基于粒子群优化算法和人工鱼群算法的混合算法,它通过模拟粒子的迁徙和鱼群的觅食行为来搜索最优解。在多式联运路径优化问题中,粒子群AFO算法可以用来搜索最优的路径组合,以最小化总运输距离。算法的基本思想是通过不断迭代和更新粒子的位置来寻找更优的解决方案。
综上所述,帝国企鹅算法、遗传算法和粒子群AFO算法都是有效的工具,可以用来求解多式联运路径优化问题。这些算法的基本思想都是通过模拟自然界的行为来搜索最优解。然而,每种算法都有其特点和适用范围,因此在实际应用中需要根据具体情况选择合适的算法。
多式联运路径优化问题是一个具有挑战性的任务,但是通过合理地选择和应用优化算法,我们可以找到最优的解决方案,提高物流效率和降低成本。希望本篇博文能够帮助读者更好地理解多式联运路径优化问题,并为实际应用提供一些有价值的参考。如果您对这一领域感兴趣,可以进一步研究和探索相关的算法和方法。
⛄ 部分代码
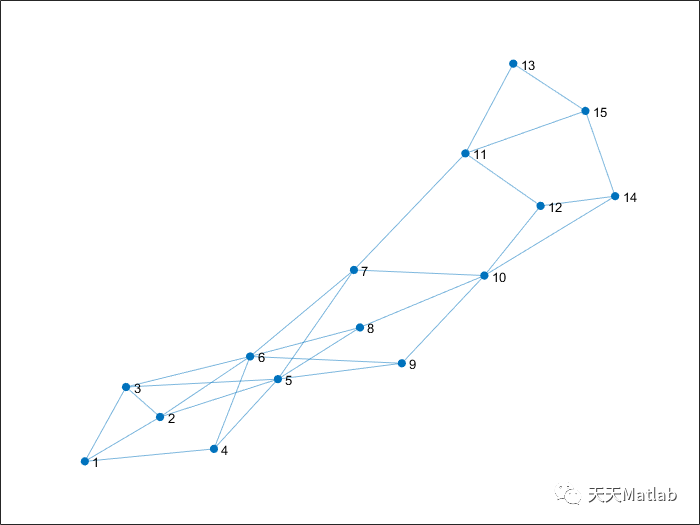
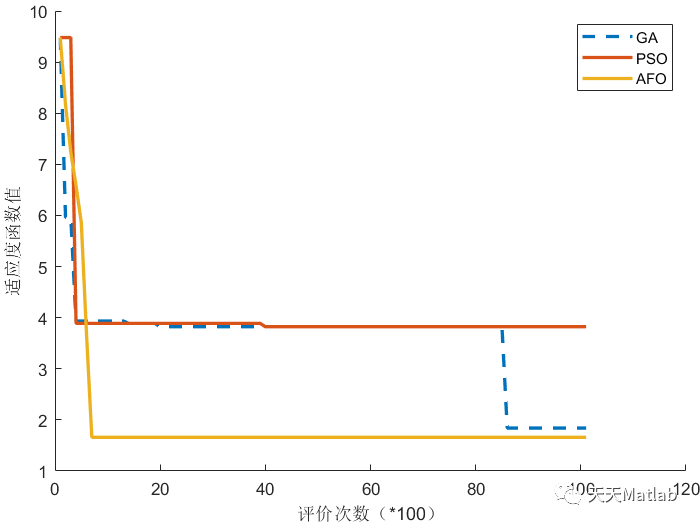
clc;clear all;close all;warning off%%noRng=1;rng('default')rng(noRng)%%global datadata.numN=15; %节点数量data.Cap_Ts=xlsread("节点处的最大中转运输能力.xlsx");temp=round(rand(data.numN,3)*10+15)*10;data.Cap_Ts(:,2:end)=temp;data.Windows=xlsread("节点的时间窗.xlsx");data.D=xlsread("节点间距离.xlsx");data.Cap_Tp=xlsread("节点间最大运输能力.xlsx");data.T=data.D;data.v=[76,60,30];for i=1:length(data.Cap_Tp(:,1))no1=data.Cap_Tp(i,1);no2=data.Cap_Tp(i,2);for j=1:3if isnan(data.Cap_Tp(i,2+j))data.D(i,2+j)=nan;endenddata.T(i,[3,6,9])=round(data.D(i,3:5)./data.v/1.2);data.T(i,[4,7,10])=round(data.D(i,3:5)./data.v);data.T(i,[5,8,11])=round(data.D(i,3:5)./data.v/0.8);enddata.Windows(:,3)=data.Windows(:,3).*(1-rand(size(data.Windows(:,3))));data.Windows(:,4)=data.Windows(:,4).*(1+rand(size(data.Windows(:,3))))+10;data.Windows(:,3:4)=max(0,round(data.Windows(:,3:4)+randn(size(data.Windows(:,3:4)))));data.Windows(:,5)=max(data.Windows(:,4));data.CT=[0,3.09,5.23; % 转换成本3.09,0,26.62;5.23,26.62,0];data.TT=[0,1,1; %转换时间1,0,2;1,2,0];data.ET=[0,1.56,6; % 转换碳排放1.56,0,3.12;6,3.12,0];data.q=[120,150,180];data.E0=[0.796,0.028,0.04];data.CW=[30,50];data.S=1;data.E=15;data.alpha=0.8;data.beta1=0.8;data.beta2=0.8;data.beta3=0.8;data.C0=[0.3,0.2,0.1]; %三种运输方式的运输成本data.weight=[1,1];data.maxB=100000;data.maxE=21000;%%%%data.numQ=100;for i=1:data.numQif rand<0.5data.q0(i)=rand*(data.q(2)-data.q(1))+data.q(1);elsedata.q0(i)=rand*(data.q(3)-data.q(2))+data.q(2);endend%%G=graph(data.D(:,1),data.D(:,2),data.D(:,1)*0+1);figureplot(G)set(gca,'LooseInset',get(gca,'TightInset'))%%lb=0;ub=1;dim=length(data.D(:,1))*3;option.lb=lb;option.ub=ub;option.dim=dim;if length(option.lb)==1option.lb=ones(1,option.dim)*option.lb;option.ub=ones(1,option.dim)*option.ub;endoption.fobj=@aimFcn_1;option.showIter=0;%% 算法参数设置 Parameters% 基本参数option.numAgent=20; %种群个体数 size of populationoption.maxIteration=100; %最大迭代次数 maximum number of interation%% 遗传算法option.p1_GA=0.7;option.p2_GA=0.1;%% 粒子群option.w_pso=0.1;option.c1_pso=1.2;option.c2_pso=1.2;%% AFOoption.v_lb=-(option.ub-option.lb)/4;option.v_ub=(option.ub-option.lb)/4;option.w2=0.5; %weight of Moving strategy IIIoption.w4=1;%weight of Moving strategy IIIoption.w5=1;%weight of Moving strategy IIIoption.pe=0.01; % rate to judge Premature convergenceoption.gap0=ceil(sqrt(option.maxIteration*2))+1;option.gapMin=5; % min gapoption.dec=2; % dec of gapoption.L=10; % Catastrophe%% DEoption.F=0.5;option.CR=0.5;%%str_legend=[{'GA'},{'PSO'},{'AFO'}];aimFcn=[{@GA},{@PSO},{@AFO3}];%% 初始化rng(noRng)x=ones(option.numAgent,option.dim);y=ones(option.numAgent,1);for i=1:option.numAgentx(i,:)=rand(size(option.lb)).*(option.ub-option.lb)+option.lb;y(i)=option.fobj(x(i,:),option,data);end%% 使用算法求解bestX=x;for i=1:length(aimFcn)rng(noRng)tic[bestY(i,:),bestX(i,:),recording(i)]=aimFcn{i}(x,y,option,data);tt(i)=toc;end%% 绘制迭代曲线figurehold onfor i=1:length(aimFcn)if i>1plot((recording(i).bestFit),'LineWidth',2)elseplot((recording(i).bestFit),'--','LineWidth',2)endendlegend(str_legend)xlabel('评价次数(*100)')ylabel('适应度函数值')set(gca,'LooseInset',get(gca,'TightInset'))%% 计算结果for i=1:length(str_legend)str=[str_legend{i},'优化后方案'];[~,result(i)]=option.fobj(bestX(i,:),option,data);% drawPC(result(i),data,str)end%%rng(11)x0=[0.227391667368465 0.879816756512174 0.758978072405287 0.510838515791228 0.192188536212261 0.651441269146713 0.418963422194475 0.552435663022093 0.692178644766480 0.525121273337296 0.901443303774014 0.870433999021102 0.727907836575027 0.635555150728710 0.377948489141470 0.0665747380900594 0.380375322185706 0.271295139005737 0.556390072117235 0.836324594294146 0.412650509862244 0.435408044462144 0.339160221282954 0.517673083186858 0.305139543163461 0.759153928221489 0.661651047625365 0.695663261206050 0.579862243307374 0.0203768757943083 0.567587976562174 0.417560315118765 0.194865572678659 0.0355023446924871 0.0656090882042756 0.283822647397696 0.409304642722500 0.797371466667136 0.139734109717042 0.943567670211017 0.736340144724420 0.899302180486718 0.0958418793238567 0.494947220485218 0.377043083335839 0.392090901825893 0.872224588221799 0.225018973369553 0.658496649609525 0.985772242893824 0.312242936944674 0.0176752228038184 0.151305501546866 0.117920480497746 0.137344184189911 0.929080746036836 0.737056036783124 0.264583371593473 0.935709972806256 0.930542122124921 0.458371373498295 0.0216966409045397 0.0615124906604629 0.569072523079761 0.912715979600965 0.684016483416011 0.0872976004423956 0.854123989826840 0.699891878132857 0.603233918882651 0.626266466189881 0.764357628595205 0.633979476955922 0.162893341780099 0.277411062836412 0.839224723775726 0.908550538167801 0.890586782754062 0.466391769502905 0.488448750263230 0.365236675941588 0.730292329677324 0.748971571306197 0.706903738180738];gs = GlobalSearch;problem = createOptimProblem('fmincon','x0',x0,...'objective',@(x)aimFcn_1(x,option,data),'lb',x0*0,'ub',x0*0+1);x = run(gs,problem);[fit1,result(i+1)]=aimFcn_1(x,option,data);%%P=[0.610000000000000 1 1 1 1 0.6100000000000000.610000000000000 1 1 0.810000000000000 0 00.830000000000000 0.920000000000000 1 1 0.900000000000000 0.8300000000000001 1 1 0.930000000000000 1 0.930000000000000]; %注 P是从result里面复制出来的str_legend=[str_legend,{'GS'}];figurebar(0:5,P,'grouped')legend(str_legend)xlabel('约束')ylabel('满足概率')set(gca,'LooseInset',get(gca,'TightInset'))
⛄ 运行结果
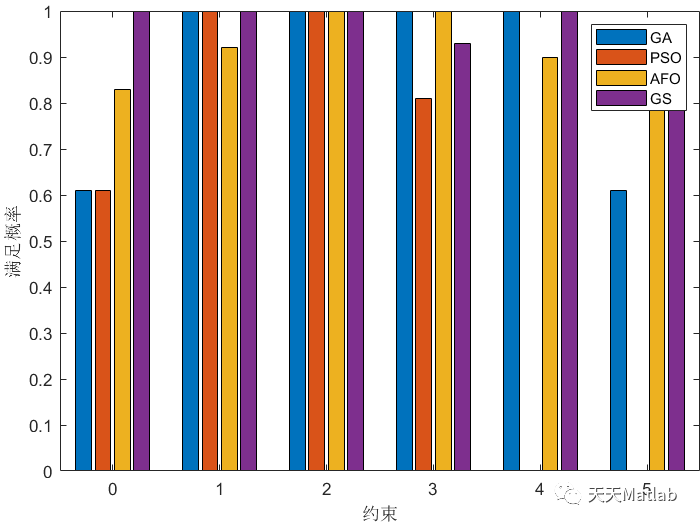
⛄ 参考文献
[1] 杨哲,邓力宝,邸元柱等。基于模糊需求和模糊运输时间的多式联运路径优化[J/OL]. 控制理论与应用:1-9[2023-07-14].http://kns.cnki.net/kcms/detail/44.1240.tp.20230612.0913.016.html.





 本文介绍了如何运用帝国企鹅算法、遗传算法和粒子群AFO算法解决多式联运路径优化问题,通过模拟自然界的决策过程寻找最优路径组合,以提高运输效率和降低成本。
本文介绍了如何运用帝国企鹅算法、遗传算法和粒子群AFO算法解决多式联运路径优化问题,通过模拟自然界的决策过程寻找最优路径组合,以提高运输效率和降低成本。

















 145
145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










