Ti-55511合金高应变率变形行为

关注

原创 2025-10-14 03:36:51 1.4k 阅读 AI 写同款· GEO 优化 ›

Ti‐5Al‐5Mo‐5V‐1Cr‐1Fe合金高应变率变形中的微观结构演化

摘要

为研究Ti‐5Al‐5Mo‐5V‐1Cr‐1Fe（Ti‐55511）合金在高应变率剪切变形中的微观结构演化，采用分离式霍普金森压杆结合“应变冻结”技术对帽形试样进行了一系列强制剪切试验。这些试验在Ti‐55511合金中诱发了局部化剪切带。实验结果表明，帽形试样中的流动应力保持恒定（约600兆帕），且与冲压深度无关。绝热剪切带的宽度随冲压深度的增加而增大，并趋于在 30 µm处饱和，同时对帽形（HS）试样中绝热剪切带（ASB）宽度的估算进行了修正。基于实验结果，热软化对绝热剪切带的起始及动态再结晶的形成影响较小，动态再结晶的形核机制为应变诱导晶界迁移以及亚晶粒旋转与合并。此外，我们提出了将粘着断裂作为Ti‐55511合金的动态失效机制的概念。

关键词

Ti‐55511合金；强制剪切试验；绝热剪切带；动态再结晶；剪切带宽度

引言

“绝热剪切带”（以下简称ASB）这一术语自首次在泽纳和霍洛蒙的原始报告 1944[1]中提出以来，已被研究人员广泛接受。ASB是固体材料在高应变率变形中的重要失效机制，尤其对于钛合金而言[2]。

钛合金优异的物理性能，如高比强度、良好的淬透性和出色的裂纹扩展抗力，使其成为航空航天、医疗设备和汽车工业应用中极具吸引力的材料[3–6]。在过去二十年中，已开展了大量关于钛合金在高应变率加载条件下的研究[7–11]。Meyers 等人[7]发现，在商业纯钛（TA2）帽形（HS）试样中，实测绝热剪切带宽度与 Bai 等人[12]及多德和白[13,14],提出的准则所计算的预测值之间存在三倍差异，而在陈等人[15]的研究中，实测绝热剪切带宽度略高于计算值。Rittel 等人[9],观察到尺寸为10–30 nm的纳米晶粒，而 Meyers 等人[7]则观察到约200 nm的亚晶粒。

Ti‐5Al‐5Mo‐5V‐1Cr‐1Fe（Ti‐55511）合金是一种典型的近‐β‐型钛合金，由于其与Ti‐6Al‐4V （TC4）合金相比可减重15–20%，因此作为飞机结构材料具有优越性[16]。

最近五年对Ti‐55511合金进行了大量研究，其中大多数集中在材料制备[17–20]。梁等人[21]发现，在热变形过程中，Ti‐55511合金的再结晶体积分数可以量化为动态再结晶 (DRX) 相对于动态回复机制的净软化效应。南等人[22]指出，应变率对DRX演化的影响是决定应变速率敏感性的主要因素。然而，梁等人和南等人的研究结果均基于低应变率加载条件（<50 s−1）。仅有少数研究报道了Ti‐55511合金在动态力学性能方面的表现（>100 s−1）[16]。尽管绝热剪切的主要机制是硬化效应（应变和应变率）与热软化效应之间的竞争，但整个过程非常复杂，涉及高应变率、局部高温、大塑性变形等因素[2]。

事实上，Ti‐55511钛合金的力学行为极为复杂，且对应变和应变率等加载条件高度敏感[23]。

Ti‐55511合金在动态变形过程中的力学行为和微观结构演化仍尚未被充分理解。

本研究的目的是深入理解：（a）Ti‐55511合金在强制剪切试验中的动态力学行为和微观结构演化；（b）基于白[12]以及多德和白[13,14]提出的剪切带半宽准则，测量与计算所得绝热剪切带宽度之间的关系。

2. 材料与方法

本研究所用的Ti‐55511合金来自中国航发集团有限公司(AECC)北京航空材料研究院，为直径 155 mm的锻棒。通过金相观察法测得收到的棒材的 β‐transus温度约为1163 K。该合金的化学成分列于表1中。有关该材料的更多信息此前已有描述[16]。

表1. Ti‐5Al‐5Mo‐5V‐1Cr‐1Fe合金的化学成分（重量%）

Al	Mo	V	Cr	Fe	C	N	H	O	Zr	Si	Ti
5.50	4.82	4.82	1.02	1.02	0.02	0.03	0.001	0.1	0.15	0.10	余量

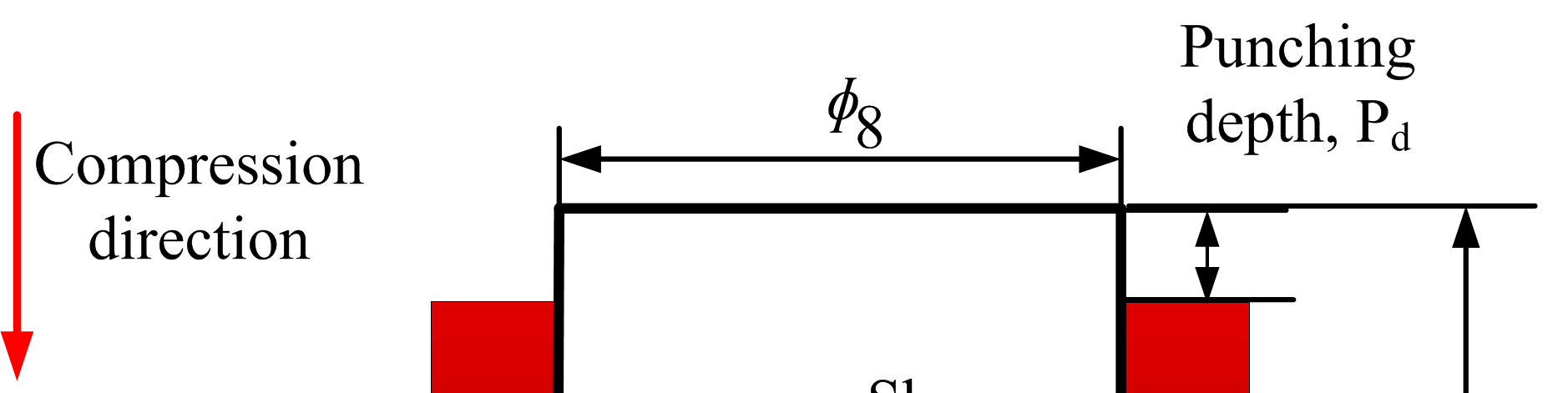
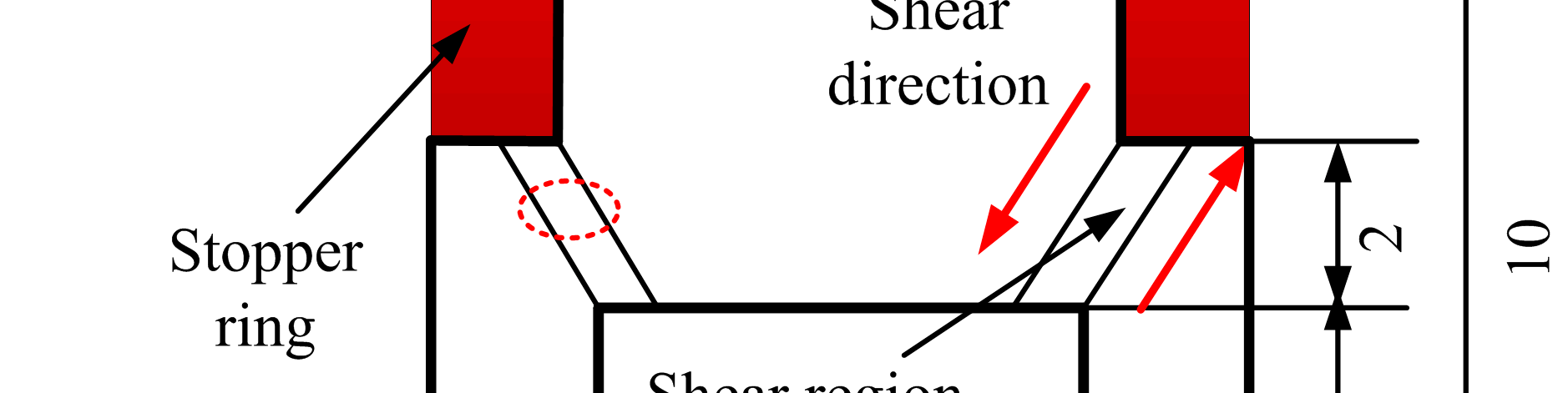
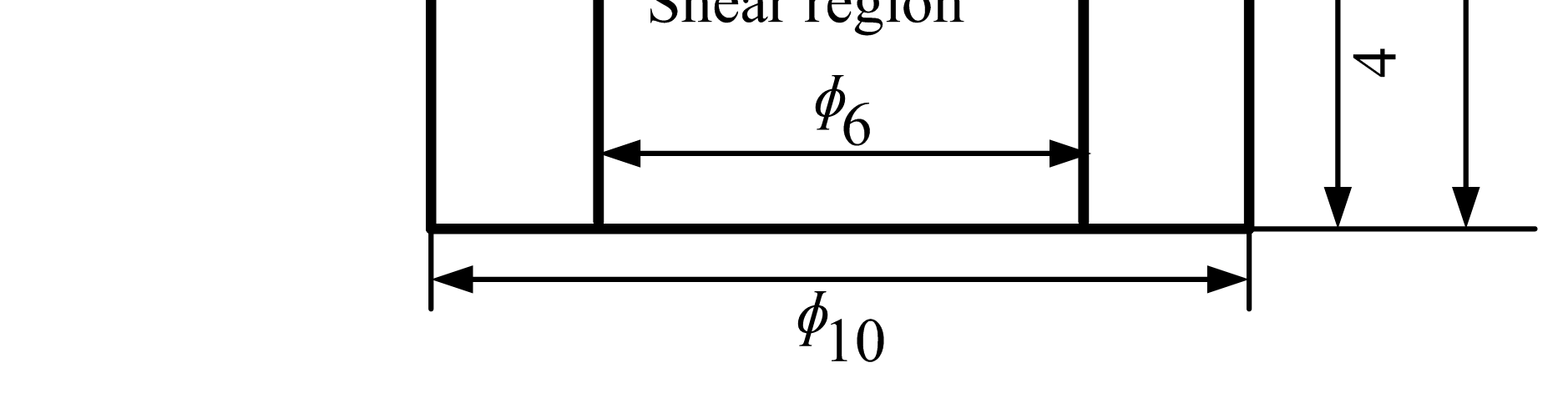
采用分离式霍普金森压杆（SHPB，西北工业大学航空学院，中国西安）技术，在293 K下对帽形（HS）试样进行了一系列动态强迫剪切试验[7,24]。这种特殊设计的试样结构可在变形过程中形成受控良好的局部化剪切带区域，已被成功应用于金属在强制局部剪切条件下大应变、高应变率变形的研究[15,25–27]。在SHPB试验中，样本被夹在入射杆和透射杆之间。使用高强度钢限位环以确保主塑性变形区域达到规定位移（见图1）。HS试样由锻棒经电火花加工（EDM）（江苏泰州创源机床有限公司，泰州，中国）和数控铣床（河北华岳机械制造有限公司，邢台，中国）加工而成，实验装置的详细信息此前已有描述[16]。通过改变冲压深度（Pd），即限位环厚度，获得不同的剪切应变，如图1所示。设定Pd的值分别为0.7、0.8、0.9、1.0和1.1 毫米。需要指出的是，杆件与试样接触面进行了充分润滑，以减少摩擦和试样鼓胀。还应指出，本研究仅关注ASB形成后Ti‐55511合金的微观结构演化，每种加载条件使用三个HS试样。撞击杆速度v可通过光电二极管（a）之间的距离除以数据采集仪器记录的时间（t）计算得出。塑性变形区域的应力状态非常接近纯剪切加载。

示意图0

用于显微组织观察的样本通过电火花加工沿变形方向平行切割，金相试样经标准机械抛光后用克罗尔试剂腐蚀。扫描电子显微镜（SEM）和透射电子显微镜（TEM）试样从不同的加载条件制备，以实现对显微组织的对比表征。观察重点位于剪切区域中心（图1中所示的虚线圆）。用于透射电镜观察的样品首先被抛光至厚度约为 50 µm，然后从样品上仔细穿孔制备出直径3毫米的薄片，随后在Gatan 691（Gatan公司，美国加利福尼亚州普莱森顿拉斯波西塔斯大道）精密离子抛光系统中进行离子束铣削，初始离子能量为5千电子伏特，最后在3千电子伏特离子能量下完成终抛光。光学显微镜（OM）和SEM检测分别在LEICA DMI 3000M Kirana‐05M（徕卡显微系统CMS有限公司，德国韦茨拉尔）和日立S‐4800（日立高新技术公司，日本东京都千代田区）上进行。TEM观察在FEI Tecnai G2‐F30（FEI公司，美国俄勒冈州希尔斯伯勒）透射电子显微镜中以200千伏工作电压进行。

3. 结果与讨论

3.1. 力学试验

当杆中产生一维应力波且试样处于均匀应力状态时，作用力F（分布在HS试样上表面）和试样中的冲压深度Pd可由下式确定：

$$
F_s(t) = \frac{A_0 E_0 [\varepsilon_i(t) + \varepsilon_r(t) + \varepsilon_t(t)]}{2}, \quad (1)
$$

$$
P_d = C_0 \int_0^t \varepsilon_r(t) dt, \quad (2)
$$

其中A₀是杆的横截面积，E₀和C₀分别是杆材料的杨氏模量和弹性杆波速。此处，εᵢ(t)、εᵣ(t)和εₜ(t)分别表示在试样端处杆中的入射、反射和透射应变历史。

然后，可以估算HS试样的剪切应力（τₛ）、整体剪切应变（γ）、局部剪应变（γ_loc）和局部剪切应变率（$\dot{\gamma}_{loc}$）如下：

$$
\tau_s(t) = \frac{2\sqrt{5}E_0 A_0 \varepsilon_t(t)}{5A_s}, \quad (3)
$$

$$
\gamma = \frac{P_d}{t_D}, \quad (4)
$$

$$
\gamma_{loc} = \frac{P_d}{t_M}, \quad (5)
$$

$$
\dot{\gamma}_{loc} = \frac{v}{2t_M}, \quad (6)
$$

其中 Aₛ 为样本的初始横截面积，t_D 和 t_M 分别为剪切区域的设计宽度（约1 mm，图1中所示虚线圆）和实测剪切带宽度。

剪切应力可以转换为正应力（σ），公式如下：

$$
\sigma = 2\tau. \quad (7)
$$

剪切变形持续时间可以从实验数据中直接确定。如图2a所示进行了SHPB试验。在冲压深度为1.1毫米时，试样的剪切变形持续时间约为100 μs。所有冲压深度下的剪切应力与冲压深度关系曲线如图2b所示，由于波在试样表面和止动环处的反射，所有曲线均表现出振荡现象。此外，这些曲线在不同冲压深度下均显示出一个平台区，并且在接触钢制止动环时剪切应力急剧增加。值得注意的是，不同冲压深度下的流动应力几乎为常数，约为600兆帕，表明Ti‐55511合金的流动应力与冲压深度无关。

因此，Ti‐55511合金的相应正应力可取为1200兆帕。然而，在我们之前的研究中，Ti‐55511合金在动态压缩下的圆柱形试样中的正应力约为1500兆帕[23]。因此，HS试样中的相应正应力比圆柱形试样低约300兆帕。这种差异可能是由于HS试样的几何缺陷所致。

示意图1 HS样品在1.1毫米冲压深度下剪切应力随时间的变化曲线。约100 μs的时间窗口表示剪切带变形阶段；(b) 剪切应力随不同规定冲压深度的变化曲线。注意当达到规定位移时，曲线的上升趋势。)

3.2. 显微组织表征

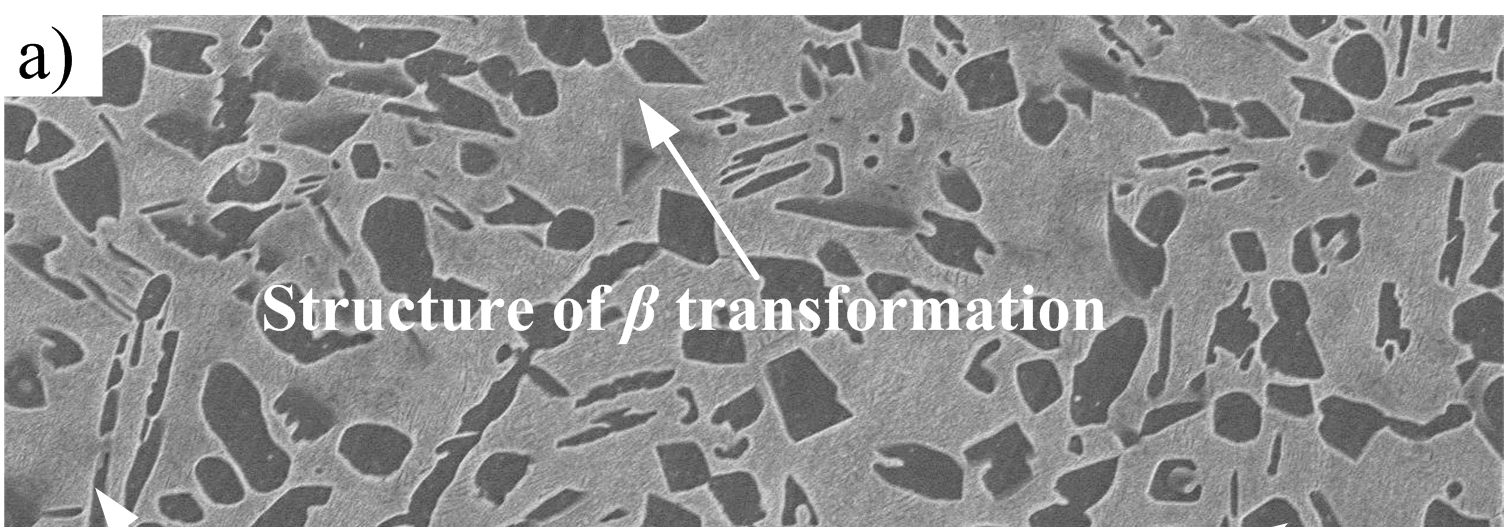
未变形试样的典型扫描电镜显微照片如图3a所示。图3b为 β‐转变（基体）结构的高倍透射电子显微镜显微照片，其中可观察到许多较薄的片状 α‐相。如图3所示，Ti‐55511合金的初始微观结构由 β‐转变（基体）和α‐相（片状α以及等轴状α）组成，等轴α的尺寸约为 4 µm。

示意图2 扫描电镜显微照片和(b) β转变组织的透射电镜显微照片)

典型低倍光学显微照片显示了发育良好的局部剪切带，如图4所示。图4b–d 是图4a中区域“A”的高倍放大图像。如图4所示，剪切带宽度的值在20–28 µm范围内。冲压深度为0.8毫米时，HS试样剪切变形区的典型扫描电镜显微照片如图5所示。图5a显示了一个带有相关裂纹的绝热剪切带，图5a中区域“A”的高倍显微照片如图5b所示。

示意图3 无止动环；(b) Pd= 1.0 mm；(c) Pd= 0.9 mm；(d) Pd= 0.7 mm。)

示意图4

如图4和图5所示，α相由于强烈的剪切变形沿剪切方向被拉长。沿剪切方向被拉长的“等轴”α相尺寸约为5–6 µm，大于未变形试样（图2a）中4 µm的初始尺寸。随着进一步变形，被拉长的α相在剪切带内或靠近剪切带处破碎成细小结构。此外，剪切带与周围变形结构之间存在一条非常明显边界。需要注意的是，尽管裂纹在一定程度上延伸进入绝热剪切带（图4d），但几乎所有裂纹均出现在剪切带/基体界面处。类似现象在Ti‐55511合金中也已观察到[16,28,29]。每种加载条件下的绝热剪切带宽度均被测量并绘制于图6中。结果表明，绝热剪切带宽度随整体剪切应变（冲压深度）的增加而增大，并在约30µm处趋于饱和。所测得的宽度与白等人[30]以及多德和白[13],提出的公式预测值进行了比较，相关内容将在第3.3节中讨论。

结合我们之前的工作 [16,29] 以及图4和图5所示的显微组织，可以总结Ti‐55511合金绝热剪切带内微观结构演化的序列，示意图如图7所示。如图7a所示，由于剪切区域发生严重应变集中而形成绝热剪切带，靠近绝热剪切带的晶粒或相沿剪切方向旋转并伸长（见图4和5）。随后，微裂纹在剪切带/基体界面形核（图7b），相邻微裂纹合并成更大裂纹（图7c）。随着进一步变形，裂纹以两种方式扩展。其一是裂纹沿剪切带/基体界面扩展（图7d），直至失效或断裂（图7g）。另一个是裂纹扩展进入绝热剪切带，并沿剪切带/基体界面（图7e,f）扩展，直至失效或断裂（图7h）。值得注意的是，Ti‐55511合金中绝热剪切带演化的特征与粘着断裂相似。因此，“粘着断裂”可被确定为Ti‐55511合金的动态失效机制[29]。

示意图5

示意图6 ：绝热剪切带形成；(b)：微裂纹形成（剪切带/基体界面处的红点）；(c)：相邻微裂纹合并；(d)：沿剪切带/基体界面的裂纹扩展；(e,f)：裂纹扩展进入绝热剪切带；(g,h)：最终断裂。)

绝热剪切带内及附近的显微组织通过透射电子显微镜进行表征，不同冲压深度下剪切区域的特征微观结构如图8所示。如图2b所示，未变形的Ti‐55511合金的初始微观组织中晶体内的位错密度较低。与Ti‐55511合金的初始微观结构相比，随着剪切变形的进行，可观察到平面平行位错和位错偶极子（见图8a）。由于位错沿剪切方向运动，当冲压深度增加至0.8毫米时，形成竹节状偶然位错边界（见图8b）。当冲压深度进一步增加至0.9毫米时，来自不同滑移系的位错开始缠结并堆积，从而形成胞状结构（见图8c,d）。这些由宽边界界定的小区域或胞体表现出非常少或没有单独的位错。此外，可以清楚地观察到位错堆积群和层错。拉长的胞状结构的破裂也可以在图8d中看到（由虚线圆标记）。由于观察平面平行于剪切方向，因此拉长胞体的三维形状预期为“煎饼”状。Meyers 等人[7]报道了类似的结果。随着进一步变形（Pd= 1.0 mm），一些晶粒和/或相被破碎成尺寸约为60–90 纳米的亚晶粒。显然，这些亚晶粒基本不含位错。对于单次冲击试验（使用无止动环的分离式霍普金森压杆强制剪切的样品），由于严重剪切变形，具有小取向差的相邻亚晶粒会通过旋转至重合来降低其表面能，从而消除分隔它们的小角度晶界[27,31]。由于相邻亚晶粒的旋转和聚合，可观察到尺寸约为6 纳米的纳米晶粒（见图8f）。选区衍射图样显示不完整环，表明存在动态再结晶（DRX，由箭头标出）。这与Rittel 等人[9]报道的结果一致。

示意图7 Pd = 0.7 mm，(b) Pd = 0.8 mm，(c) Pd = 0.9 mm，(d) Pd = 0.9 mm，(e) Pd = 1.0 mm 和 (f) 无止动环。)

3.3. 绝热剪切带宽度的估算

利用扰动分析已令人满意地预测了绝热剪切带宽度[13,14]。这些分析中包含了热传导对剪切带厚度的贡献[30]。白等人[30]以及多德和白[2,13,14],给出了绝热剪切带宽度的一个非常简单的估算方法。

$$
\delta = 2\sqrt{\frac{\lambda T_{\text{max}}}{\beta \tau \dot{\gamma}_{\text{loc}}}}, \quad (10)
$$

其中 $\delta$ 为剪切带宽度，$\lambda$ 和 $T_{\text{max}}$ 分别为剪切带内的热导率和最高温度。对于 Ti‐55511 合金，$\lambda$ 等于 9.21 W/(m·K)。

Ti‐55511合金在HS试样中的剪切应力估计为恒定的600兆帕。然后，绝热剪切带宽度可视为 $\sqrt{T_{\text{max}}/\dot{\gamma} {\text{loc}}}$ 的线性函数。表2列出了每次试验的绝热剪切带计算值以及计算值与测量值之比。图9显示了绝热剪切带宽度随 $\sqrt{T {\text{max}}/\dot{\gamma}_{\text{loc}}}$ 的变化关系。结果表明，使用公式(9)预测的绝热剪切带宽度远小于实验结果。

表2。整体剪切应变、局部剪切应变率、最高温度和绝热剪切带宽度的总结

Pd/mm	v/ms⁻¹	t_M/µm	t_D/mm	γ	γ_loc	$\dot{\gamma}_{loc}$/s⁻¹	T_max/K	δ/µm	δ/t_M
0.7	23.8	20.1	1.01	0.693	34.83	5.92 × 10⁵	454	6.86	2.93
0.8	23.7	23.2	1.03	0.777	34.48	5.11 × 10⁵	467	7.49	3.10
0.9	23.7	25.5	1.02	0.882	35.29	4.65 × 10⁵	494	8.08	3.16
1	23.7	27.3	1.01	0.990	36.63	4.34 × 10⁵	504	8.44	3.23
1.1	23.5	27.9	1.04	1.058	39.43	4.21 × 10⁵	532	8.81	3.17
无止动环	23.8	28.2	1.02	1.196	46.10	4.22 × 10⁵	573	9.13	3.09

约 6–9 μm [23]。Meyers 等人 [7] 和陈等人 [15] 计算了HS试样中不同材料的绝热剪切带宽度，并给出了不同的结果。Meyers 等人在TA2中观察到实验观测结果与计算值之间存在三倍差异，而陈等人报告称，实验观察到的宽度略微高于钽的计算值。在本研究中，测得的绝热剪切带宽度约为计算结果的两倍。尽管王等人 [28] 未使用公式(9)计算绝热剪切带的厚度，但在他们的研究中，计算得到的绝热剪切带宽度约为实测值的1/3（H4样品）。因此，对于Ti‐55511合金，测得的绝热剪切带厚度与计算值之间存在约三倍的差异。因此，高速下绝热剪切带宽度的计算可修正为：

$$
\delta_M = 2k\sqrt{\frac{\lambda T_{\text{max}}}{\tau \dot{\gamma}_{\text{loc}}}}, \quad (11)
$$

其中 $k$ 是系数。

示意图8 和修正公式(11)的理论预测结果作为对比。)