第一章 函数与极限 第四节 无穷小与无穷大

第四节 无穷小与无穷大

一、无穷小

定义1 如果函数 $f(x)$ 当 $x\to x_0$ (或 $x\to \infty$) 时的极限为零，那么称函数 $f(x)$ 为当 $x\to x_0$ (或 $x\to \infty$) 时的无穷小.

注意： 无穷小 $\ne$ 很小的数.

定理1 在自变量的同一变化过程 $x\to x_0$ (或 $x\to \infty$)中，函数 $f(x)$ 具有极限 $A$ 的充分必要条件是 $f(x)=A+\alpha$，其中 $\alpha$ 是无穷小.

---

二、无穷大

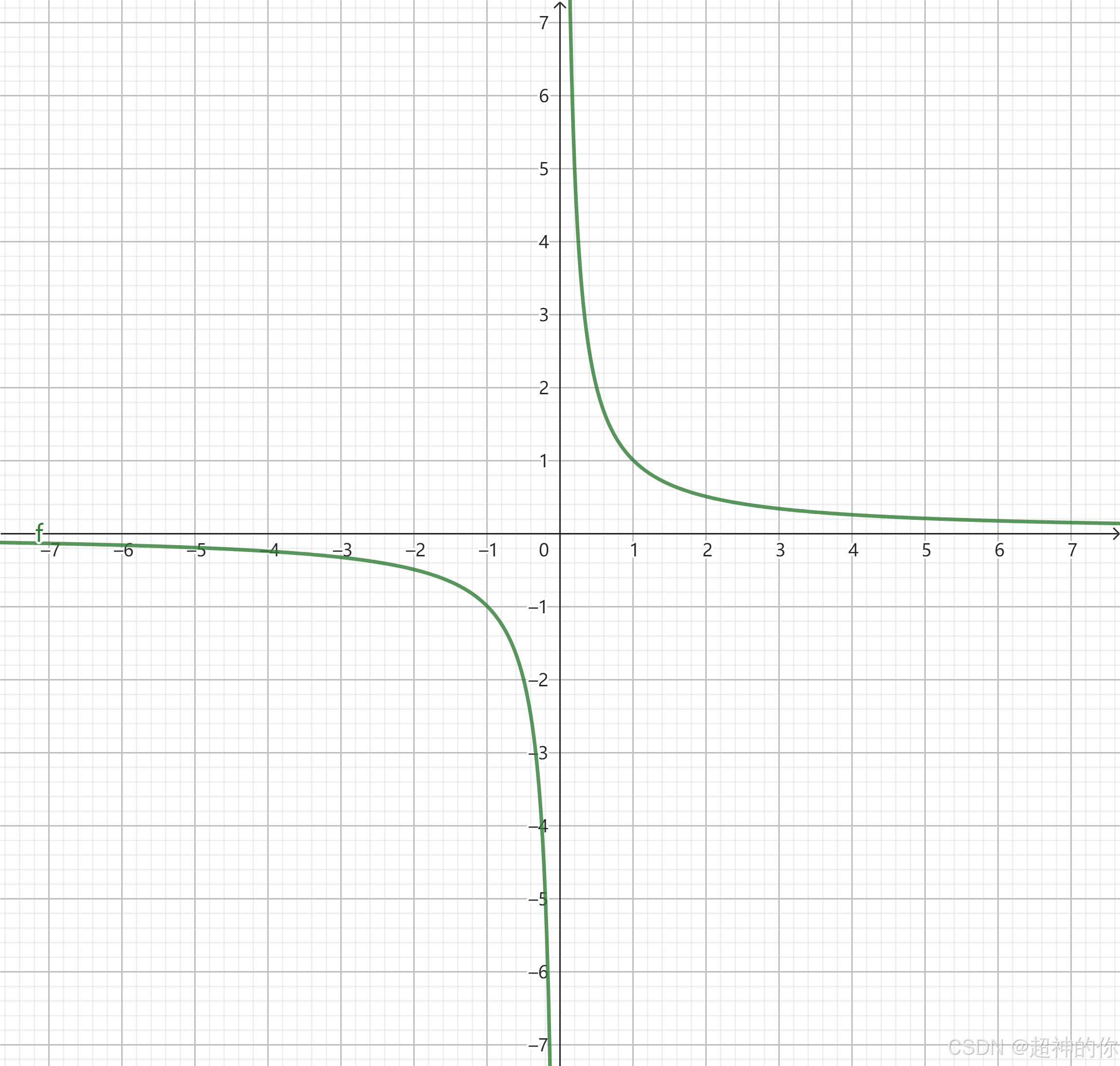
定义2 设函数 $f(x)$ 在 $x_0$ 的某一去心邻域内有定义 (或 $|x|$ 大于某一正数时有定义). 如果对于任意给定的正数 $M$ (无论它多么大)，总存在正数 $\delta$ (或正数 $X$)，只要 $x$ 适合不等式 $0<|x-x_0|<\delta$ (或 $|x|>X$)，对应的函数值 $f(x)$总满足不等式$$|f(x)|>M,$$那么称函数 $f(x)$ 是当 $x\to x_0$ (或 $x\to \infty$) 时的无穷大.

为便于叙述，“函数的极限是无穷大” 记作：$$\underset{x\to x_0}{\lim }f(x)=\infty (或\underset{x\to \infty }{\lim }f(x)=\infty ).$$

注意： 无穷大 $\ne$ 很大的数.

定理2 在自变量的同一变化过程中，如果 $f(x)$ 为无穷大，那么 $\frac{1}{f(x)}$ 为无穷小；反之，如果 $f(x)$ 为无穷小，且 $f(x)\ne 0$，那么$\frac{1}{f(x)}$为无穷大.

---

习题1-4