Stanley算法 | Python源码

目录

一、算法介绍

二、转向角计算

三、算法本质：

四、调试中可能遇到的问题

五、python源码

一、算法介绍

        Stanley是一种基于几何路径的轨迹追踪控制器，其设计理念是将参考点设置在前轮中心，这种设计方式可以使算法能够在路径跟踪过程中实现全局收敛，其误差衰减速率不随车辆速度变化而变化。实验表明，以前轮中心为参考点的控制器性能优于以重心或后轮重心为参考线的控制器。

        在没有前视距离的情况下，直接根据前轮中心参考点来考虑横向误差以及航向角误差。

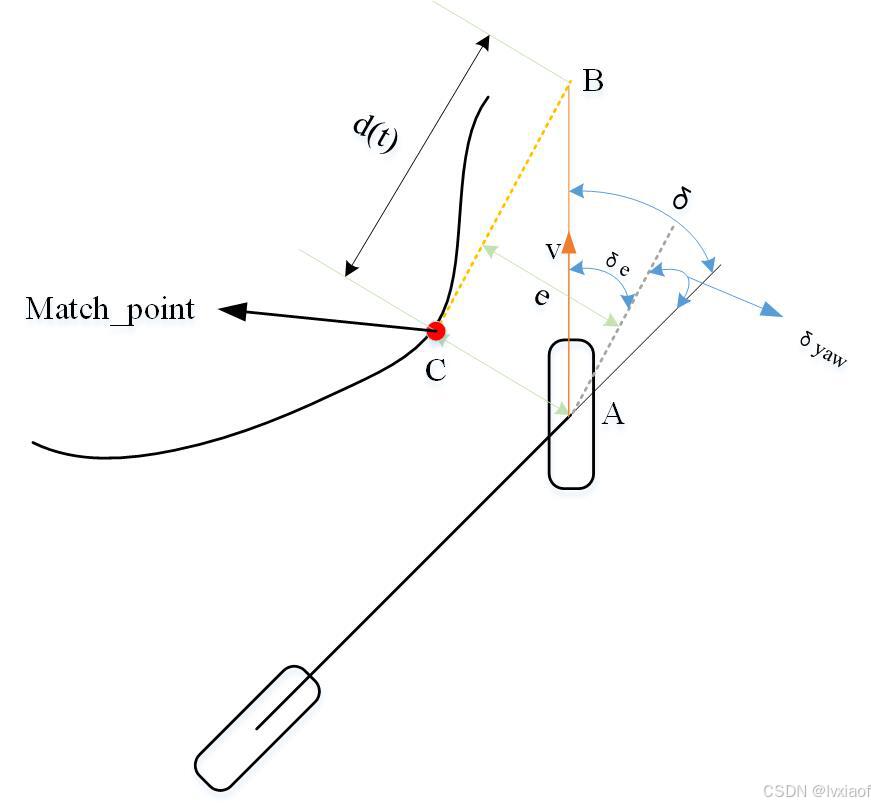
图1 Stanley模型

        Stanley控制器中主要考虑了横向误差与航向误差，上图中，车身航向角与参考点航向角的差值定义为，前轮与最近点的横向距离定义为e。

二、转向角计算

1. 消除航向角误差

自行车模型中，想让车头对准那个方向，需要前轮也需要对准某个方向，可以认为前轮转角与航向角近似相等：

前轮转角很小的情况下：

可以直接认为是一个增益系数

2. 消除横向产生的航向误差

在三角形ABC中：

d认为是人为给定的一个预瞄距离，认为和速度正相关

故：

综上得到

三、算法本质：

横向误差变化率：

横向误差逐渐减小，故横向误差变化率为负（如第一帧为2，第二帧为1，变化率为负）

在三角形ABC中：

带入

故：

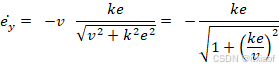
横线误差很小时：

积分得：

t趋于无穷时，横向误差以指数形式收敛于0，k越大收敛越快

四、调试中可能遇到的问题

1. 弯道过冲问题：
       Stanley只依赖航向误差与横向误差进行补偿，没有考虑前方曲率信息，可以将前方曲率作为前馈加入航向误差中，即：

2. 高速弯道中可能会因为横向偏差过大引起航向角变化较快：

引入将k值与速度进行关联，速度值越大，减缓回归速度

横向误差进行软化，避免横向误差线性放大：

五、python源码

from Reference_Line import MyreferencePath
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter
import math
import time as tm

max_steer = math.radians(30.0)  # [rad] max steering angle
dt = 0.05 
L = 2.7   #轴距
class State:
    def __init__(self,x = 0.0, y = 0.0, theta = 0.0, v = 0.0):
        self.x = x
        self.y = y
        self.theta = theta
        self.v = v
        
def update_state(State, delta):
    if delta > max_steer:
        delta = max_steer
    elif delta < -max_steer:
        delta = -max_steer
        
    State.x = State.x + State.v * math.cos(State.theta) * dt
    State.y = State.y + State.v * math.sin(State.theta) * dt
    State.theta = State.theta + State.v / L * math.tan(delta) * dt
    State.theta = MyreferencePath.modpi(State.theta)
    State.v = State.v
    
    return State

def find_match_point_idx(state,referpath):
    min_dis = 1e6
    match_idx = -1
    for i in range(len(referpath)):
        cur_dis = math.sqrt((referpath[i].x - state.x) **2 + (referpath[i].y - state.y) **2)
        if cur_dis < min_dis:
            min_dis = cur_dis
            match_idx = i
            
    return match_idx

def calc_lat_dis(match_idx,state,referpath):

    dx = state.x - referpath[match_idx].x
    dy = state.y - referpath[match_idx].y
    lat_dis = dy * referpath[match_idx].cos_theta - dx * referpath[match_idx].sin_theta#SL坐标系

    return lat_dis

def stanley_plan(veh_state,referpath,match_idx,e,tagert_theta,k):
    delta_yaw = MyreferencePath.modpi(tagert_theta - veh_state.theta)
    delta_lat = -math.atan2(k * e , veh_state.v)
    delta_ff  = math.atan(L * referpath[match_idx + 5].k)
    
    delta = delta_yaw + delta_lat + delta_ff
    
    return delta

def main():
    time = 0.0
    refline = MyreferencePath()
    ref_num = len(refline.refer_path)
    veh_state = State(x=0,y=-2,theta=0,v=20)
    dis_from_veh_to_refend = math.sqrt(
        (veh_state.x - refline.refer_path[ref_num - 1].x) **2 + 
        (veh_state.y - refline.refer_path[ref_num - 1].y) **2)

    #k越小,d越大，因距离误差产生的航向误差越小
    coeffi_k = 1
    # 初始化绘图
    plt.ion()  # 开启交互式绘图
    fig, ax = plt.subplots(figsize=(10, 6))  # 宽10英寸，高6英寸
    ax.set_aspect('equal')
    ax.grid(True)
    ax.set_title("Stanley Path Tracking")
    ax.set_xlabel("X [m]")
    ax.set_ylabel("Y [m]")
    ax.set_xlim(-10, 120)  # 根据你的数据范围调整
    ax.set_ylim(-10, 10)
    # 提前画好参考线
    ref_x = [p.x for p in refline.refer_path]
    ref_y = [p.y for p in refline.refer_path]
    ax.plot(ref_x, ref_y, 'k--', label='Reference Line')
    # 绘制车辆轨迹（实时更新）
    veh_x, veh_y = [], []
    veh_plot, = ax.plot([], [], 'r-', label='Vehicle Path')
    veh_point, = ax.plot([], [], 'bo', label='Vehicle Position')

    ax.legend()
    
    while time < 10:
        match_idx = find_match_point_idx(veh_state,refline.refer_path)
        if match_idx == -1:
            raise ValueError('没有找到匹配点')
    
        e = calc_lat_dis(match_idx, veh_state, refline.refer_path)
        target_theta = refline.refer_path[match_idx].theta
        
        #stanley规划
        target_delta = stanley_plan(veh_state,refline.refer_path,match_idx,e,target_theta,coeffi_k)
        
        #车辆状态更新
        veh_state = update_state(veh_state,target_delta)
        
        #时间、位置更新
        time += 0.05
        dis_from_veh_to_refend = math.sqrt(
            (veh_state.x - refline.refer_path[ref_num - 1].x) **2 + 
            (veh_state.y - refline.refer_path[ref_num - 1].y) **2)
        if dis_from_veh_to_refend < 1:
            break
        # 记录轨迹点
        veh_x.append(veh_state.x)
        veh_y.append(veh_state.y)
        # 动态更新绘图
        veh_plot.set_data(veh_x, veh_y)
        veh_point.set_data(veh_state.x, veh_state.y)
        plt.pause(0.05)  # 暂停以更新图像
        tm.sleep(0.01)   # 控制动画速度，可调小或调大
        
    plt.ioff()  # 关闭交互模式
    plt.show()  # 最终展示完整轨迹
    
if __name__ == "__main__":
    main()
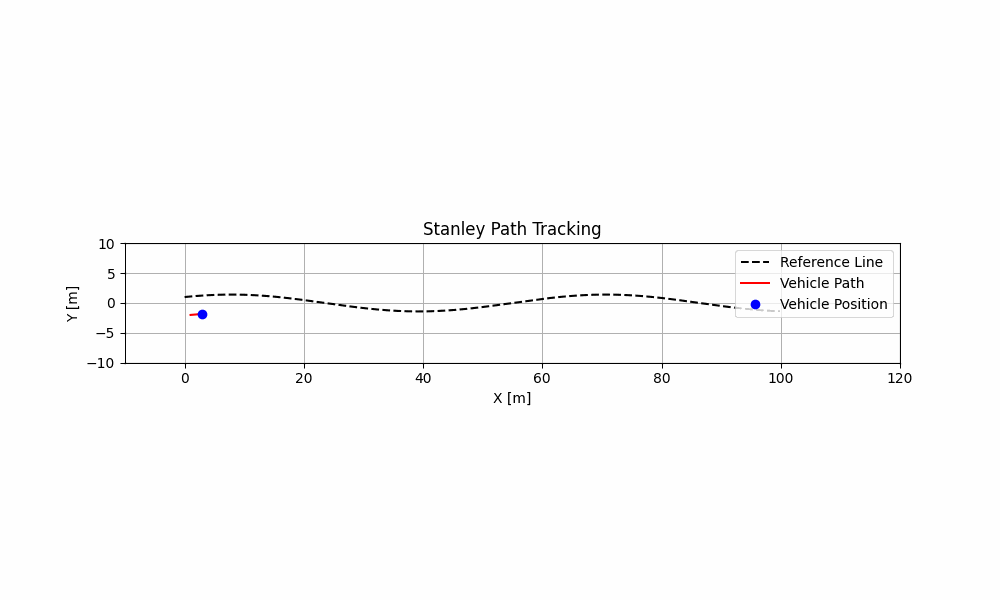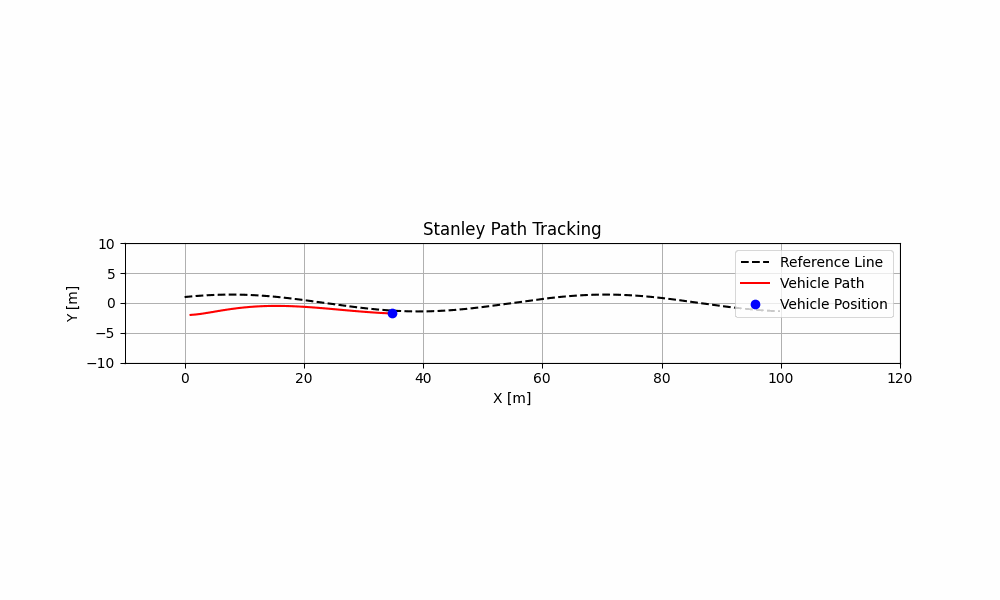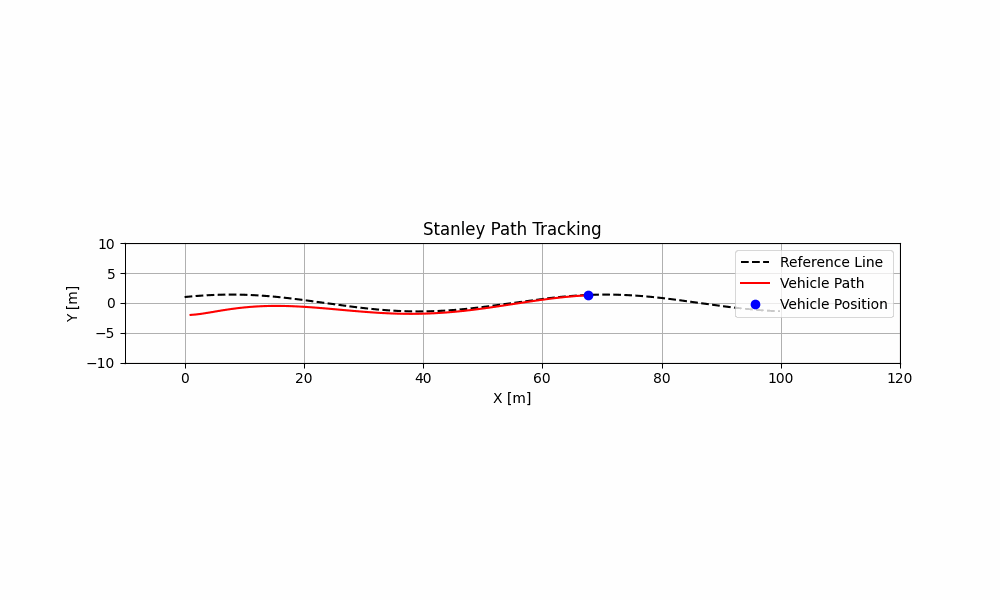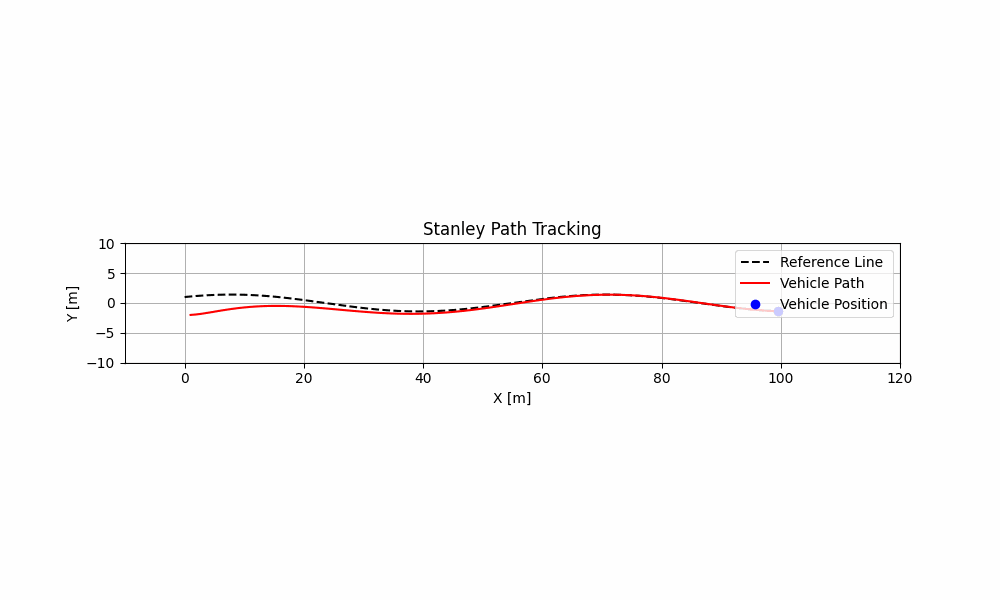
    print('处理完成.')

最终跟踪效果图：