目录
参考博客：
Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）
车辆动力学模型
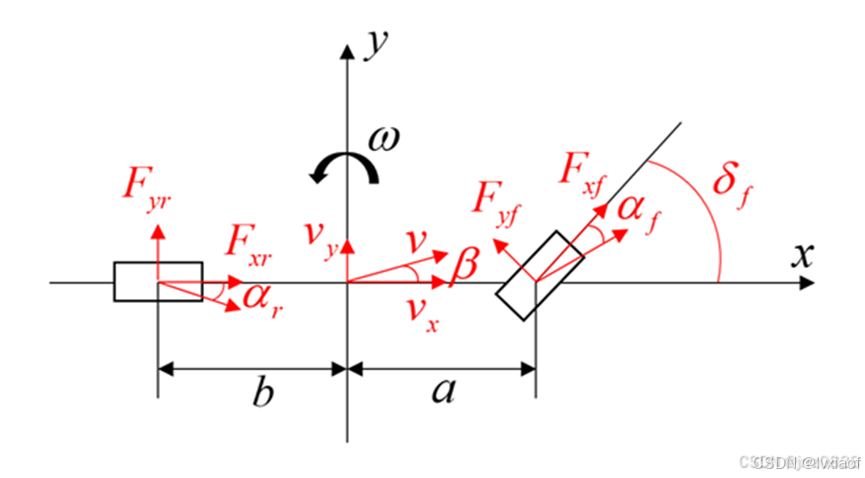
图1 车辆二自由度模型
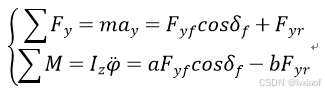
（1）
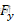为y轴方向合力，
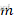为车辆质量，
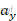为沿y轴的加速度，
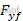为前轮轮胎侧偏力，
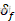为前轮转角，
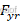为后轮轮胎侧偏力；
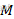为合力矩，
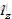为转动惯量，
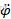为角加速度，
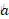为车辆质心到前轴的距离，b为车辆质心到后轴的距离。
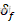值较小，
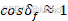，得
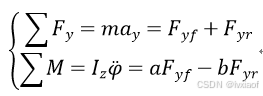
（2）
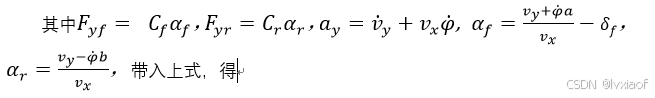
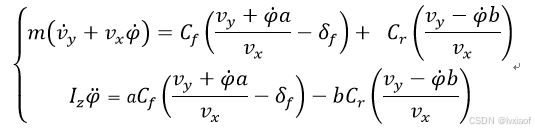
（3）
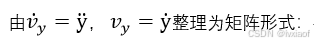
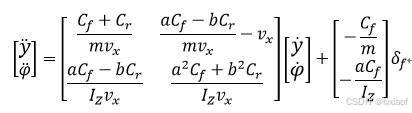
（4）
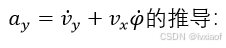
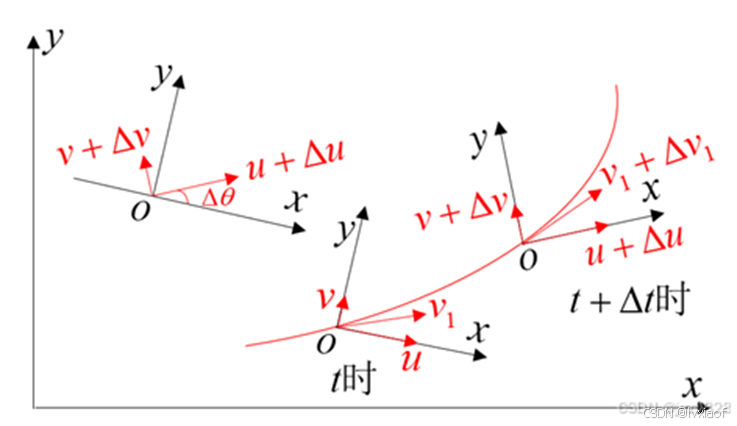
图2 速度变化示意图
如上图所示：车辆沿ox轴、oy轴的速度变化量为
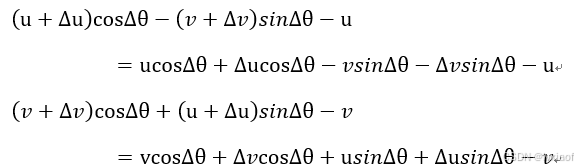
（5）
考虑到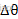
很小并忽略其中的二阶量，
，
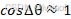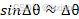
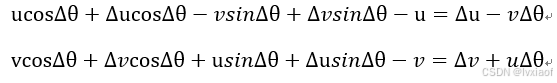
（6）
所以车辆沿质心的加速度分量分别为：
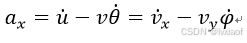
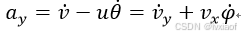
（7）
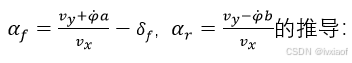
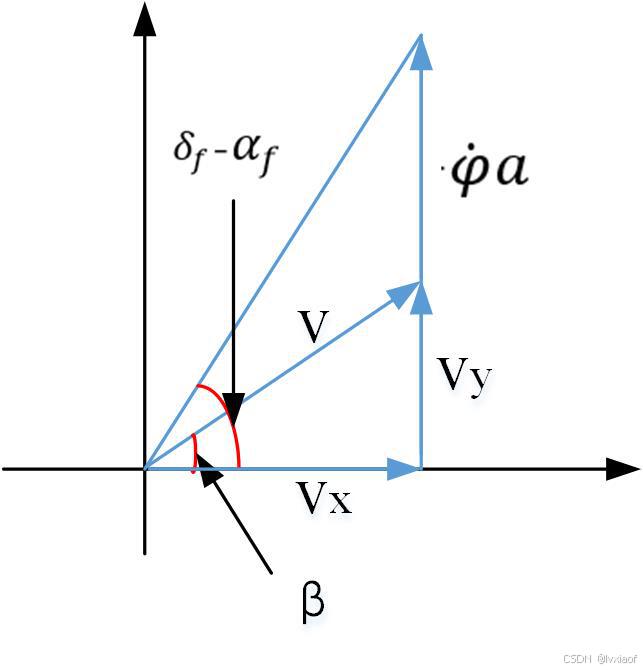
图3 前轮角度平移到质心
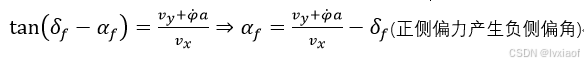
（8）
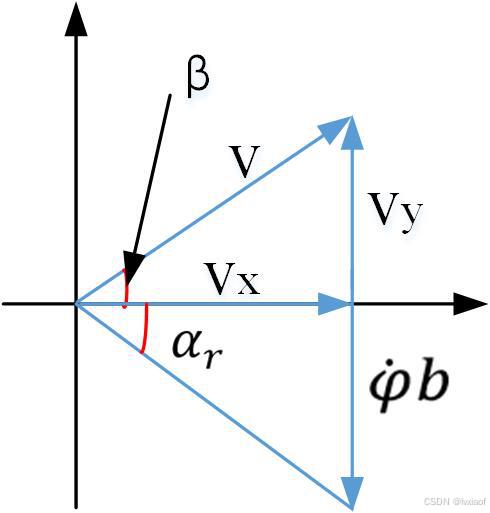
图4 后轮角度平移到质心
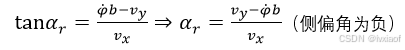
（9）
横向误差模型
式（4）为车身坐标系的状态方程，不可直接使用，需转换到SL坐标系。
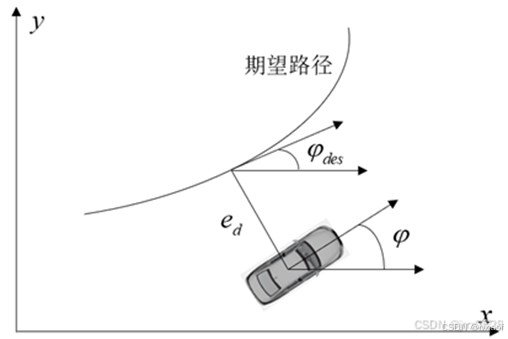
图5 横向误差模型示意图
在式（4）的基础的上，令航向角误差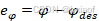
，则：
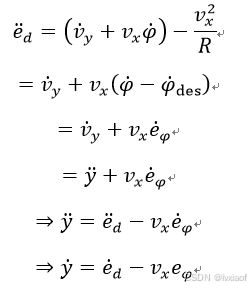
（10）
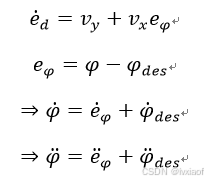
（11）
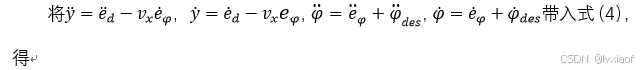
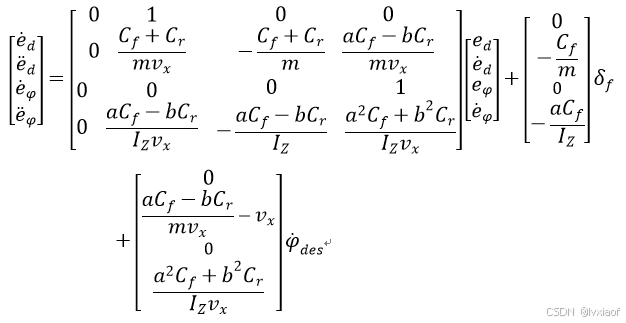
（12）
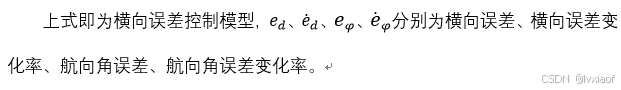
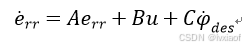
（13）
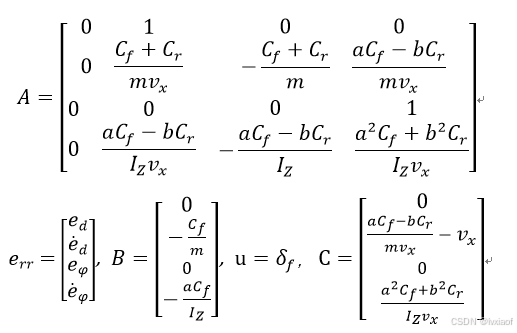
以上推导基于正侧偏力产生负侧偏角，因APOLLO影响过于强大，特给出基于APOLLO中的状态空间方程：
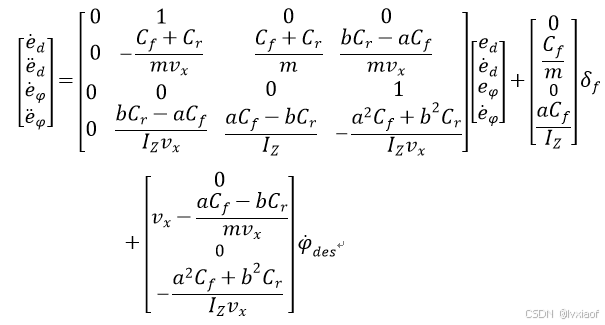
（14）
状态空间方程离散化
以下推导基于apollo状态空间方程，对状态空间方程进行离散化，第一个采用中点欧拉法，第二个采用向前欧拉法。
连续方程离散化的数学推导：
故：离散化后方程变为:
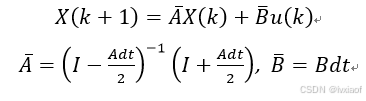
LQR前馈计算
对于一个系统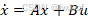
进行反馈控制，令
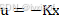，即可使得系统稳定，但是在横向误差控制模型中，多了一部分
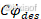，若进行反馈控制，
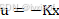，则式（13）变为：
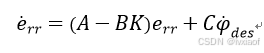
（15）
由式（15）可知，无论K取何值，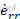
和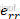
都无法同时为0，系统存在稳态误差。因此为消除稳态误差带来的影响，考虑在反馈控制的基础上加入前馈控制，引入前馈值
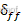，通过选取适当的前馈值来使得稳态误差尽可能趋近于0，控制量变为如下形式：
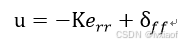
（16）
则式（13）变为
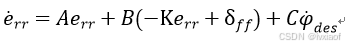
（17）
系统稳定后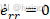
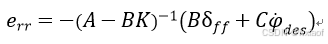
（18）
最后求得：
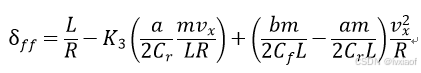
（19）
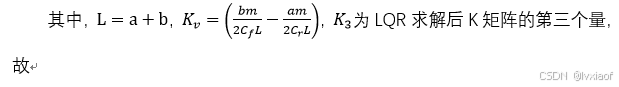
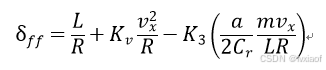
（20）
最后前轮转角：
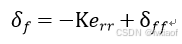
（21）
状态量err的计算
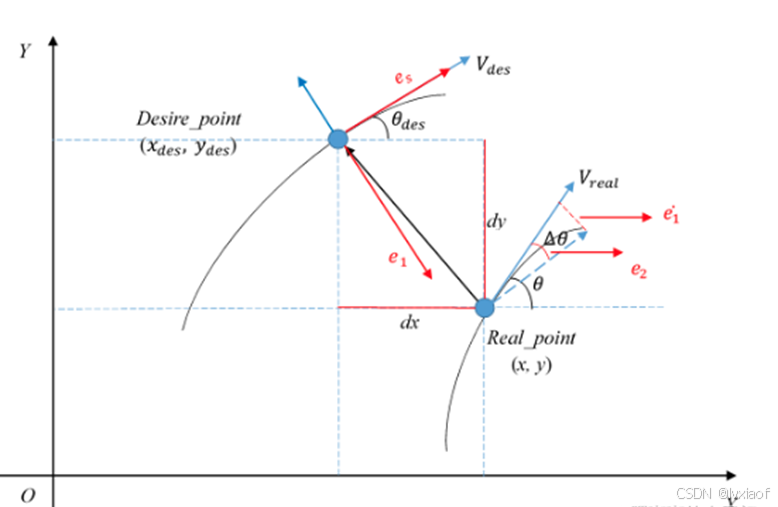
图6 坐标转换示意图
笛卡尔坐标系中：
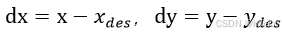
（22）
ed本质含义就是SL坐标系下车辆与参考轨迹的距离横向距离L,将车辆转到参考点坐标系，故
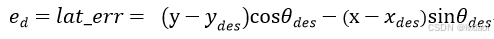
（23）
// 横向控制
const double dx = x - target_point.path_point().x();
const double dy = y - target_point.path_point().y();
const double cos_target_heading = std::cos(target_point.path_point().theta());
const double sin_target_heading = std::sin(target_point.path_point().theta());
double lateral_error = cos_target_heading * dy - sin_target_heading * dx;
double heading_error =
common::angles::normalize_angle(theta - model_state.reference_yaw);
double lateral_error_dot = linear_v * std::sin(heading_error);
double target_heading_rate =
target_waypoint.curvature() * target_waypoint.velocity();
double heading_error_rate = angular_v - target_heading_rate;
C++实现
轨迹构造
#include "reference_line.h"
MyReferencePath::MyReferencePath()
{
int i = 0;
double dx = 0.0, dy = 0.0;
double ddx = 0.0, ddy = 0.0;
refer_path.point.resize(1000);
//生成参考线轨迹
for (i = 0; i < 1000; i++)
{
refer_path.point[i].x = 0.1 * i;
//refer_path.point[i].y = sin(refer_path.point[i].x / 4.0) + cos(refer_path.point[i].x / 4.0);
refer_path.point[i].y = 1.0;
refer_x.push_back(refer_path.point[i].x);
refer_y.push_back(refer_path.point[i].y);
}
//计算航向角、曲率
for (i = 0; i < refer_path.point.size(); i++)
{
if (i == 0)
{
dx = refer_path.point[i + 1].x - refer_path.point[i].x;
dy = refer_path.point[i + 1].y - refer_path.point[i].y;
ddx = refer_path.point[2].x + refer_path.point[0].x - 2 * refer_path.point[1].x;
ddy = refer_path.point[2].y + refer_path.point[0].y - 2 * refer_path.point[1].y;
}
else if (i == refer_path.point.size() - 1)
{
dx = refer_path.point[i].x - refer_path.point[i - 1].x;
dy = refer_path.point[i].y - refer_path.point[i - 1].y;
ddx = refer_path.point[i].x + refer_path.point[i - 2].x - 2 * refer_path.point[i - 1].x;
ddy = refer_path.point[i].y + refer_path.point[i - 2].y - 2 * refer_path.point[i - 1].y;
}
else
{
dx = refer_path.point[i + 1].x - refer_path.point[i].x;
dy = refer_path.point[i + 1].y - refer_path.point[i].y;
ddx = refer_path.point[i + 1].x + refer_path.point[i - 1].x - 2 * refer_path.point[i].x;
ddy = refer_path.point[i + 1].y + refer_path.point[i - 1].y - 2 * refer_path.point[i].y;
}
refer_path.point[i].theta = atan2(dy, dx);
//计算曲率:设曲线r(t) =(x(t),y(t)),则曲率k=(x'y" - x"y')/((x')^2 + (y')^2)^(3/2).
refer_path.point[i].k = (ddy * dx - ddx * dy) / pow((dx * dx + dy * dy), 3 / 2);
}
}
/**
* 计算跟踪误差
* @param robot_state 机器人状态
* @return
*/
vector<double> MyReferencePath::calcTrackError(Veh_State &robot_state)
{
double x = robot_state.veh_x, y = robot_state.veh_y;
vector<double> d_x(refer_path.point.size()), d_y(refer_path.point.size()), d(refer_path.point.size());
int i = 0;
for (i = 0; i < refer_path.point.size(); i++)
{
d_x[i] = refer_path.point[i].x - x;
d_y[i] = refer_path.point[i].y - y;
d[i] = sqrt(d_x[i] * d_x[i] + d_y[i] * d_y[i]);
}
double min_idx = min_element(d.begin(), d.end()) - d.begin();
double yaw = refer_path.point[min_idx].theta;
double k = refer_path.point[min_idx].k;
double angle = normalizeAngle(yaw - atan2(d_y[min_idx], d_x[min_idx]));
double error = d[min_idx];//误差
if (angle < 0)
{
error *= -1;
}
return{ error, k, yaw, min_idx };
}
/**
* 角度归一化
* @param angle
* @return
*/
double MyReferencePath::normalizeAngle(double angle) {
while (angle > PI) {
angle -= 2.0 * PI;
}
while (angle < -PI) {
angle += 2.0 * PI;
}
return angle;
}LQR求解器
#include "LQRControl.h"
LQRControl::LQRControl(int n) : N(n) {};
/**
* 解代数里卡提方程
* @param A 状态矩阵A
* @param B 状态矩阵B
* @param Q Q为半正定的状态加权矩阵, 通常取为对角阵；Q矩阵元素变大意味着希望跟踪偏差能够快速趋近于零；
* @param R R为正定的控制加权矩阵，R矩阵元素变大意味着希望控制输入能够尽可能小。
* @return
*/
MatrixXd LQRControl::calRicatti(MatrixXd A, MatrixXd B, MatrixXd Q, MatrixXd R)
{
MatrixXd Qf = Q;
MatrixXd P = Qf;
MatrixXd P_;
for (int i = 0; i < this->N; i++)
{
P_ = Q + A.transpose() * P * A - A.transpose() * P * B * (R + B.transpose() * P * B).inverse() * B.transpose() * P * A;
if ((P_ - P).maxCoeff() < EPS && (P - P_).maxCoeff() < EPS)
{
break;
}
P = P_;
}
return P_;
}
/**
* LQR控制器
* @param robot_state
* @param refer_path
* @param s0
* @param A
* @param B
* @param Q
* @param R
* @return
*/
vector<MatrixXd> LQRControl::lqrControl(Veh_State &vehcle_state,
Refer_Path refer_path,
int idx, MatrixXd A, MatrixXd B,
MatrixXd Q, MatrixXd R)
{
const double dx = vehcle_state.veh_x - refer_path.point[idx].x;
const double dy = vehcle_state.veh_y - refer_path.point[idx].y;
const double cos_target_heading = cos(refer_path.point[idx].theta);
const double sin_target_heading = sin(refer_path.point[idx].theta);
double lateral_error = cos_target_heading * dy - sin_target_heading * dx;
double heading_error = vehcle_state.veh_theta - refer_path.point[idx].theta;
normalizeAngle(heading_error);
double lateral_error_dot = cos(vehcle_state.veh_theta) * vehcle_state.veh_v * sin(heading_error);
//仿真时采用运动学估算车辆角速度
double veh_angular_v = vehcle_state.veh_angular;
double target_heading_rate =
refer_path.point[idx].k * refer_path.point[idx].v;
double heading_error_rate = veh_angular_v - target_heading_rate;
MatrixXd X(4, 1);
X << lateral_error, lateral_error_dot, heading_error, heading_error_rate;
MatrixXd P = calRicatti(A, B, Q, R);
MatrixXd K = (R + B.transpose() * P * B).inverse() * B.transpose() * P * A;
MatrixXd u = -K * X;
double u0 = u(0, 0);
return { K, X, u };
#endif // KinematicModel
}
/**
* 角度归一化
* @param angle
* @return
*/
double LQRControl::normalizeAngle(double angle) {
while (angle > PI) {
angle -= 2.0 * PI;
}
while (angle < -PI) {
angle += 2.0 * PI;
}
return angle;
}动力学模型
#include "Dynamic_model.h"
DynamicModel::DynamicModel(double Vx, double x, double y, double theta, double dt, double L, double v, double angular_v):
Vx(Vx), x(x), y(y),theta(theta), dt(dt), L(L), v(v), angular_v(angular_v)
{
wheelbase_ = 2.852;
C_alpha_f = 155494.663;
C_alpha_r = 155494.663;
m = 1845.0;
l_f = 2.852 / 2.0;
l_r = 2.852 / 2.0;
I_z = l_f * l_f*(m / 2.0) + l_r * l_r*(m / 2.0);
K_V = l_r * m / 2 / C_alpha_f / wheelbase_ - l_f * m / 2 / C_alpha_r / wheelbase_;
}
vector<MatrixXd> DynamicModel::GenerateStateSpace()
{
//构建的ABC矩阵中侧偏刚度为正值
MatrixXd A(4, 4), B(4, 1), C(4, 1);
A << 0, 1, 0, 0,
0, (-C_alpha_f - C_alpha_r) / (m * Vx), (C_alpha_f + C_alpha_r) / m, (C_alpha_r * l_r - C_alpha_f * l_f) / m * Vx,
0, 0, 0, 1,
0, (C_alpha_r * l_r - C_alpha_f * l_f) / (I_z * Vx), (C_alpha_f * l_f - C_alpha_r * l_r) / I_z, (-C_alpha_r * l_r * l_r - C_alpha_f * l_f * l_f) / (I_z * Vx);
B << 0,
C_alpha_f / m,
0,
C_alpha_f * l_f / I_z;
C << 0,
(C_alpha_f * l_f + C_alpha_r * l_r) / (m * Vx) - Vx,
0,
(-2 * l_f * l_f * C_alpha_f + 2 * l_r * l_r * C_alpha_r) / (I_z * Vx);
return{ A, B, C};
}
VectorXd DynamicModel::compute_X_dot(const VectorXd& state, double delta, double psi_des)
{
vector<MatrixXd> ABC = GenerateStateSpace();
MatrixXd& A = ABC[0];
MatrixXd& B = ABC[1];
MatrixXd& C = ABC[2];
MatrixXd X_dot = A * state + B * delta + C * psi_des;
//状态量为横向偏差、横向偏差变化率、航向角偏差、航向角偏差变化率
return X_dot;
}
pair<MatrixXd, MatrixXd> DynamicModel::DiscreteStateSpace(double dt)
{
auto ABC = GenerateStateSpace();
MatrixXd& A = ABC[0];
MatrixXd& B = ABC[1];
MatrixXd I = MatrixXd::Identity(4, 4);
//MatrixXd A_bar = I + A * dt;//前向欧拉法
MatrixXd A_bar = (I - A * dt * 0.5).inverse() * (I + A * dt * 0.5);//中点欧拉法
MatrixXd B_bar = B * dt;
return make_pair(A_bar, B_bar);
}
void DynamicModel::updatestate(double delta_f)
{
x = x + cos(theta) * v * dt;
y = y + sin(theta) * v * dt;
theta = theta + (v * tan(delta_f) * dt) / L;
angular_v = (v * tan(delta_f) * dt) / L;
//后续航向角可通过yaw_rate更新
}
Veh_State DynamicModel::getstate()
{
Veh_State veh_state;
veh_state.veh_x = x;
veh_state.veh_y = y;
veh_state.veh_theta = theta;
veh_state.veh_v = v;
veh_state.veh_angular = angular_v;
return veh_state;
}主函数
#include "reference_line.h"
#include "LQRControl.h"
#include "Dynamic_model.h"
int main()
{
double dt = 0.1;//时间间隔
double L = 2.852; //轴距
double veh_v = 3.0; //初始速度
double x_0 = 0.0;
double y_0 = -3.0;
double veh_theta = 0.0;
double angular_v = 0.0;
int N = 500;
int i = 0;
MatrixXd Q(4, 4);
Q << 2, 0, 0, 0,
0, 10, 0, 0,
0, 0, 1, 0,
0, 0, 0, 0.1;
MatrixXd R(1, 1);
R << 2.0;
//保存车辆运动轨迹
vector<double> x_, y_;
MyReferencePath reference_path;
DynamicModel vehcle(veh_v * cos(veh_theta), x_0, y_0, veh_theta, dt, L, veh_v, angular_v);
LQRControl lqr(N);
Veh_State veh_state = { 0 };
vector<double>target_point;
pair<MatrixXd, MatrixXd> state_space;
vector<MatrixXd> matrix_KXU;
double ref_k = 0.0, ref_yaw = 0.0;
int idx = 0;
double ref_delta = 0.0, delta = 0.0;//期望前轮转角
double steer_angle_feedforward = 0.0;
double v_x = 0.0;
double u = 0.0;
for ( i = 0; i < 500; i++)
{
veh_state = vehcle.getstate();
target_point = reference_path.calcTrackError(veh_state);//获取车辆与参考线匹配点的距离、匹配点的曲率、航向、索引。
ref_k = target_point[1];
idx = (int)target_point[3];
//ref_k = reference_path.refer_path.point[idx + 50].k;
v_x = veh_state.veh_v * cos(veh_state.veh_theta);
state_space = vehcle.DiscreteStateSpace(dt);//获取A.B矩阵
//反馈
matrix_KXU = lqr.lqrControl(veh_state, reference_path.refer_path, idx, state_space.first, state_space.second, Q, R);//计算控制量前轮转角
MatrixXd& matrix_k_ = matrix_KXU[0];
MatrixXd& matrix_X_ = matrix_KXU[1];
u = matrix_KXU[2](0,0);
//前馈
steer_angle_feedforward =
(vehcle.wheelbase_ * ref_k + vehcle.K_V * v_x * v_x * ref_k -
matrix_k_(0, 2) *
(vehcle.l_r * ref_k -
vehcle.l_f * vehcle.m * v_x * v_x * ref_k / 2 / vehcle.C_alpha_r / vehcle.wheelbase_));
delta = u + steer_angle_feedforward;
if (delta >= DELTA_MAX)
{
delta = DELTA_MAX;
}
else if (delta < DELTA_MIN)
{
delta = DELTA_MIN;
}
vehcle.updatestate(delta);
x_.push_back(vehcle.x);
y_.push_back(vehcle.y);
}
return 0;
}
扫一扫
4577
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
