目录
参考博客：
一、MPC简介
MPC是一种先进的控制算法，广泛应用于自动驾驶、机器人、工业过程等控制场景。它的核心思想是：基于系统模型，在有限预测时域内对未来行为进行优化，实施滚动求解控制输入。
1. 预测模型
使用一个已知的系统模型（如车辆动力学模型）来预测未来若干时刻的系统状态
其中，
为当前系统状态量，
为当前控制输入
2. 滚动优化
在每个控制周期（如50ms）构建一个预测时域，长度为
,设计一个代价函数，例如：
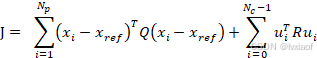
其中，
为参考轨迹或目标状态，
、
为状态和控制的加权矩阵，
为控制时域（通常小于或等于预测时域）
3. 加入约束
可以加入状态约束和输入约束，例如：
4. 求解优化问题
上述代价函数和约束组合成一个优化问题，通产是二次规划问题，求解最优控制序列：
5. 滚动执行
只执行第一个控制量
，然后进入下一个控制周期，重新获取系统状态，再次进行预测和优化。这个过程不断循环，就像一个滑动窗口，这就是“滚动优化控制”的核心思想
二、预测模型推导
离散后的车辆动力学模型：
设计新的状态量：
离散化步骤结束后进行目标函数设计，理论上，我们既可以对控制输入
直接施加代价，也可以对控制增量∆
施加代价，但是两者作用略有不同：
① 控制输入
的代价：用于限制控制输入的幅度，确保控制输入本身不超出某个合理范围。常用于限制系统的执行器工作范围，防止过大的控制信号损坏执行器。
② 控制输入
的代价：用于限制控制输入在相邻时间步之间的变化幅度，保证控制过程的平滑性和连续性，避免控制信号的跳变（也可以通过QP约束达到限制效果）。
本文控制量选取为
，在MPC中加入控制增量约束，构建新的状态量：
那么就有：
新的状态空间方程：
新的状态输出为：
预测模型推导：MPC的核心就是预测未来几个时刻的系统（运动）状态，来计算当前控制时刻的控制输入，假设有预测时域
和控制时域
，
。
......
......
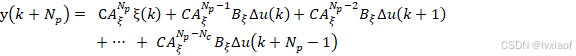
由于预测时域
通常大于控制时域
（预测未来），所以超出
部分的项，乘上的
、
、...
都等于0，所以超出
时域后面的项就不需要考虑。
上式简写：
其中：
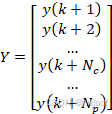
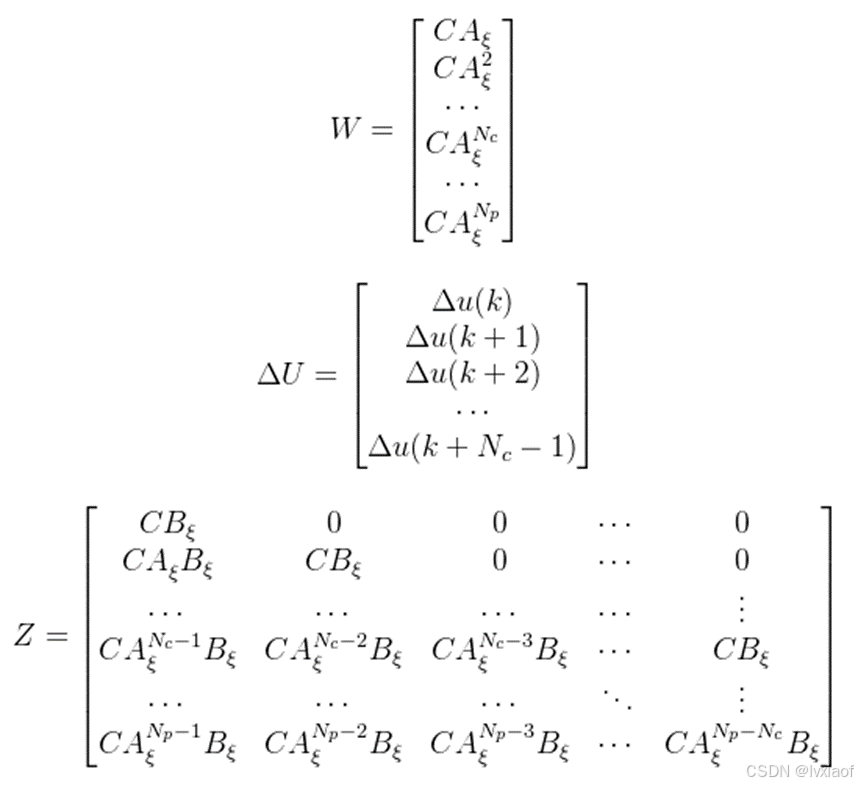
从这里观察
和
，也可以直观的推测出MPC的工作原理是根据当前的状态
，再通过给系统增加
个控制量
，就可以预测出系统的未来表现
，得到Y之后就可以根据此公式设计目标函数。
三、代价函数与约束设计
代价函数的设计目标可以归纳为以下几个方面：
最小化轨迹跟踪误差：确保车辆尽可能准确地跟踪目标轨迹。
平滑控制输入：避免过大的转向角或加速度变化，以提高驾驶平稳性和乘坐舒适性。
遵循物理限制：控制输入需要满足车辆的动力学和物理约束，例如速度、加速度和转向角的极限。
将代价函数设计为以下形式的二次型:
目标函数第一项与第三项合并起来就是完整的k时刻到Np预测时域的输出状态二次型之和，第三项单独写出来是强调终端状态误差，即在预测时域的终点 
处系统输出与参考值之间的误差的加权平方。第二项是控制增量代价项，目的是改善控制的平滑性，最后一项是引入的松弛因子，其中ρ
是一个惩罚因子，决定了违反约束的代价有多大。松弛因子
。这个项的作用是最小化违反约束的程度，确保系统尽可能满足原来的约束条件，同时避免优化失败。
约束设计：
软约束：（（soft constraints）允许在某种程度上违反，比如在急转弯或紧急避障时，可能会略微超出期望的控制输入范围或允许一定的轨迹偏离）
硬约束：（hard constraints）指的是必须严格满足的约束，例如车辆的物理限制（最大速度、最大转向角等），这些约束通常不会被放松。
控制量约束：
，
控制增量约束：
，是
因为包含了
四、优化求解
经过以上操作把误差模型转换成了线性模型，且代价函数为二次型，约束条件为线性约束，所以MPC问题可以转化为二次规划（QP）问题，用现成的二次规划求解器（如 OSQP、qpOASES 等）来进行求解；
二次规划标准公式：
1. 目标函数转化
将状态量误差代价合并，即合并第一项与第三项，并展开：
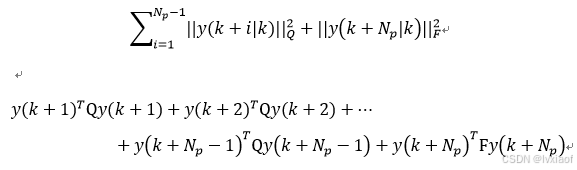
控制量误差变化量展开：
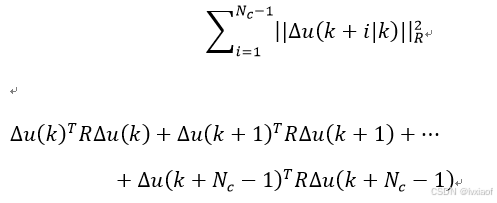
以上合并整理得：
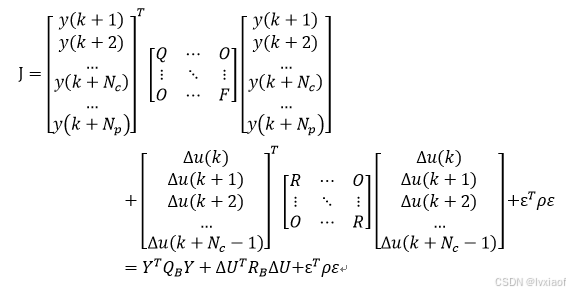
将
，且令
带入，得到：
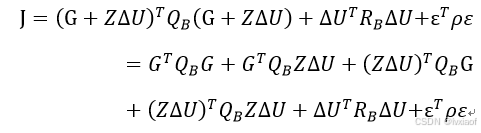
上式中第二项与第三项为转置关系，且最后是数值解，标量的转置是其本身，因此可以合并：
化为矩阵形式：
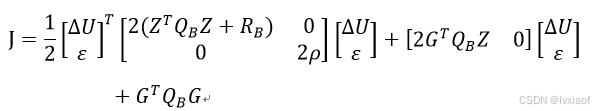
其中：
是QP中待优化的变量
是二次代价项的权重矩阵
是一次项
是常数项，不影响求解。
2. 约束转化
，
……
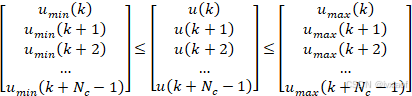
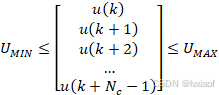
转化为矩阵形式：
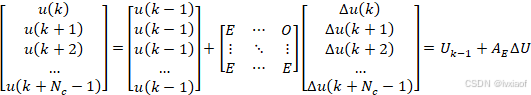
即：
转化为约束形式：
此处有疑问，既然知道了优化变量，直接施加约束不可以吗，为什么需要进行约束转换呢？
求解出优化变量x后，将优化变量的第一个值送入系统，即作用于系统的控制量为：
五、C++实现
实现时没有考虑软约束，优化变量仅为
，离散化时间间隔会显著影响精度。
#include "MPC.h"
MPCControl::MPCControl(int nx, int nu, int dt) : NX(nx), NU(nu), T(dt)
{
}
double MPCControl::linearMPCControl(Veh_State &vehcle_state, Refer_Path &refer_path, int idx,
DynamicModel &ugv, const double dt, int Np, int Nc, MatrixXd &Q, MatrixXd &Q_f, MatrixXd &R, double pre_delta)
{
PRE_U = pre_delta;
pair<MatrixXd, MatrixXd> Hf_T = setup_H_ftra(vehcle_state, refer_path, idx, ugv, dt, Np, Nc, Q, Q_f, R);
MatrixXd &H = Hf_T.first;
SparseMatrix<double> sparseH = H.sparseView();
VectorXd f_T = (VectorXd)Hf_T.second.transpose();
MatrixXd A = setup_A(Nc);
SparseMatrix<double> sparseA = A.sparseView();
pair<MatrixXd, MatrixXd> L_U = setup_L_U(Nc);
MatrixXd& L = L_U.first;
MatrixXd& U = L_U.second;
VectorXd L_Vec = (VectorXd)L;
VectorXd U_Vec = (VectorXd)U;
// Solve the optimization problem.
Solver solver;
// settings
solver.settings()->setVerbosity(true);//求解器详细输出
solver.settings()->setWarmStart(false);
// set the initial data of the QP solver
solver.data()->setNumberOfVariables(Nc); //求解变量的行
solver.data()->setNumberOfConstraints(Nc); //矩阵A的行
if (!solver.data()->setHessianMatrix(sparseH))
return 1;
if (!solver.data()->setGradient(f_T))
return 1;
if (!solver.data()->setLinearConstraintsMatrix(sparseA))
return 1;
if (!solver.data()->setLowerBound(L_Vec))
return 1;
if (!solver.data()->setUpperBound(U_Vec))
return 1;
// 初始化求解器
if (!solver.initSolver())
return 1;
//开始求解
if (solver.solveProblem() == ErrorExitFlag::NoError)
{
// 获取最优解
VectorXd solution = solver.getSolution();
std::cout << "Optimal solution:\n" << solution << std::endl;
return solution(0);
}
else
{
std::cout << "Problem failed to solve!" << std::endl;
}
return 1;
}
pair<MatrixXd, MatrixXd> MPCControl::setup_H_ftra(Veh_State &vehcle_state, Refer_Path &refer_path, int idx,
DynamicModel &ugv, const double dt, int Np, int Nc, MatrixXd &Q, MatrixXd &Q_f, MatrixXd &R)
{
//线性化矩阵AB
pair<MatrixXd, MatrixXd> AB = ugv.DiscreteStateSpace(dt);
MatrixXd& Abar = AB.first;
MatrixXd& Bbar = AB.second;
int Abar_row = Abar.rows();
int Abar_col = Abar.cols();
int Bbar_row = Bbar.rows();
int Bbar_col = Bbar.cols();
//MatrixXd matrix_C(5, 5);
//matrix_C << 1.0, 0.0, 0.0, 0.0, 0.0,
// 0.0, 1.0, 0.0, 0.0, 0.0,
// 0.0, 0.0, 1.0, 0.0, 0.0,
// 0.0, 0.0, 0.0, 1.0, 0.0;
MatrixXd matrix_C(NX, NX + NU);
MatrixXd matrix_I = MatrixXd::Identity(NX, NX);
matrix_C.block(0, 0, NX, NX) = matrix_I;
matrix_C.block(0, NX, NX, NU) = MatrixXd::Zero(NX, NU);
//矩阵Aξ
MatrixXd A_ξ(Abar_row + NU, Abar_col + Bbar_col);//5x5
A_ξ.setZero(); // 初始化为零矩阵
A_ξ.block<4, 4>(0, 0) = Abar;
A_ξ.block<4, 1>(0, 4) = Bbar;
A_ξ.block<1, 4>(4, 0) = RowVector4d::Zero();
A_ξ(4, 4) = 1;
//矩阵Bξ
MatrixXd B_ξ(Bbar_row + NU, Bbar_col);//5x1
B_ξ.setZero(); // 初始化为零矩阵
B_ξ.block<4, 1>(0, 0) = Bbar;
B_ξ(4, 0) = 1;
int ny = matrix_C.rows();//输出维度
int nu = B_ξ.cols(); //控制输入维度
int nx = A_ξ.rows(); //状态维度
int i = 0, j = 0, k = 0;
//构造Z矩阵
MatrixXd Z = MatrixXd::Zero(ny * Np, nu * Nc);
MatrixXd A_power = MatrixXd::Identity(nx, nx);
for (i = 0; i < Np; ++i)
{
//构建A_ξ幂的形式
A_power = A_ξ * A_power;
MatrixXd CA_power = matrix_C * A_power;
for (j = 0; j < Nc; ++j)
{
if (j > i)
{
break;//上三角为0
}
//计算C * A * B
MatrixXd Aij = MatrixXd::Identity(A_ξ.rows(), A_ξ.cols());
for (k = 0; k < (i - j); k++)
{
Aij = Aij * A_ξ;
}
MatrixXd block = matrix_C * Aij * B_ξ;
Z.block(ny * i, nu * j, ny, nu) = block;
}
}
//std::cout << "Z Matrix:\n" << Z << std::endl;
//构造Q_B矩阵
MatrixXd Q_B = MatrixXd::Zero(Q.rows() * Np, Q.cols() * Np);
for ( i = 0; i < Np - 1; ++i)
{
Q_B.block(Q.rows() * i, Q.cols() * i, Q.rows(), Q.cols()) = Q;
}
Q_B.block(Q.rows() * (Np - 1), Q.cols() * (Np - 1), Q.rows(), Q.cols()) = Q_f;
//std::cout << "Q_B Matrix:\n" << Q_B << std::endl;
//构造R_B矩阵
MatrixXd R_B = MatrixXd::Zero(R.rows() * Nc, R.cols() * Nc);
for ( i = 0; i < Nc; i++)
{
R_B.block(R.rows() * i, R.cols() * i, R.rows(), R.cols()) = R;
}
//std::cout << "R_B Matrix:\n" << R_B << std::endl;
//最终的H矩阵
MatrixXd H = 2 * (Z.transpose() * Q_B * Z + R_B);
//************************************************************************
//W矩阵
MatrixXd W = MatrixXd::Zero(matrix_C.rows() * Np, A_ξ.cols());
A_power = MatrixXd::Identity(nx, nx);
for ( i = 0; i < Np; i++)
{
A_power = A_power * A_ξ;
MatrixXd block = matrix_C * A_power;
W.block(matrix_C.rows() * i, 0, matrix_C.rows(), A_ξ.cols()) = block;
}
//计算状态量
const double dx = vehcle_state.veh_x - refer_path.point[idx].x;
const double dy = vehcle_state.veh_y - refer_path.point[idx].y;
const double cos_target_heading = cos(refer_path.point[idx].theta);
const double sin_target_heading = sin(refer_path.point[idx].theta);
double lateral_error = cos_target_heading * dy - sin_target_heading * dx;
double heading_error = vehcle_state.veh_theta - refer_path.point[idx].theta;
normalizeAngle(heading_error);
double lateral_error_dot = cos(vehcle_state.veh_theta) * vehcle_state.veh_v * sin(heading_error);
//仿真时采用运动学估算车辆角速度
double veh_angular_v = vehcle_state.veh_angular;
double target_heading_rate =
refer_path.point[idx].k * refer_path.point[idx].v;
double heading_error_rate = veh_angular_v - target_heading_rate;
MatrixXd ξ_k(NX + NU, 1);
ξ_k << lateral_error, lateral_error_dot, heading_error, heading_error_rate, PRE_U;
MatrixXd G = W * ξ_k;
//fT矩阵
MatrixXd f_T = 2 * G.transpose() * Q_B * Z;
return make_pair(H, f_T);
}
MatrixXd MPCControl::setup_A(int Nc)
{
MatrixXd A = MatrixXd::Zero(Nc, Nc);
for (int i = 0; i < Nc; i++)
{
A(i, i) = 1;
}
return A;
}
pair<MatrixXd, MatrixXd> MPCControl::setup_L_U(int Nc)
{
MatrixXd L = MatrixXd::Zero(Nc, 1);
MatrixXd U = MatrixXd::Zero(Nc, 1);
for (int i = 0; i < Nc; i++)
{
L(i, 0) = -MAX_DELTA_STEER;
U(i, 0) = MAX_DELTA_STEER;
}
return make_pair(L, U);
}
/**
* 角度归一化
* @param angle
* @return
*/
double MPCControl::normalizeAngle(double angle) {
while (angle > PI) {
angle -= 2.0 * PI;
}
while (angle < -PI) {
angle += 2.0 * PI;
}
return angle;
}
扫一扫
6430
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
