基于NMPC与多传感器融合的自动驾驶

基于非线性模型预测控制和多传感器融合的自动驾驶

摘要

用于控制完全自主系统的算法必须在安全性和鲁棒性方面满足极高的要求。一个特别具有挑战性的例子是自主深空任务，我们在多个项目中对此进行了研究。在此背景下，我们证明了通过结合基于不确定性扩展表示的多传感器融合与优化技术，采用非线性模型预测控制方法可以实现安全且鲁棒的自主系统。本文的重点在于通过将相应算法应用于同样极具挑战性的自动驾驶领域，展示该概念的通用性。特别是，我们基于所提出的方法论提出了一种自动驾驶汽车的系统概念。此外，我们还展示了真实世界研究车辆的实验结果，该车辆能够自主探索停车场，动态考虑障碍物，并最终完成泊车操作。

关键词 : 自动驾驶车辆, 汽车控制, 非线性模型预测控制, 车辆模型, 多传感器融合, 证据映射

1. 引言

自动驾驶车辆的发展是一个持续进行的过程，早在20世纪90年代就已取得显著成果（迪克曼斯，1997）。自那时起，工业界和学术界投入了大量努力，不断改进这一技术，最终将实现新的出行概念，提高道路安全，并实现物流过程更高程度的自动化（莫尔等人，2016）。

要实现一个完全自主系统，来自多个学术领域的专家协作至关重要。例如，车辆的安全操控应基于对其自身状态及周围环境的准确估计，以及随后对鲁棒控制指令的计算。这就催生了高度复杂的算法，例如在DARPA挑战中为自动驾驶汽车所开发的算法（弗格森等人，2008；维尔和福姆，2008）。然而，类似的要求也适用于其他截然不同的研究领域，例如KaNaRiA项目中考虑的自主深空任务（普罗布斯特等人，2015）以及EnEx‐CAUSE项目（克莱门斯等人，2018）。在此类任务中，状态估计通过贝叶斯滤波器实现（克莱门斯和席尔，2016；纳卡特等人，2018），而控制方法则基于数值优化来求解最优控制问题（沙特尔，2018；梅尔波尔等人，2018）。其结果不仅高度高效，而且显著地适用于其他场景，例如自动驾驶汽车的安全且鲁棒的控制。这一点在AO‐Car项目中得到了验证。

源自空间应用的算法在一年的时间范围内被调整，用于研究车辆进行自主停车场探索的示例场景。在本工作的后续部分，我们介绍了所形成系统的主要组件，并展示了其能力。

2. 研究车辆与系统概述

提出的系统在经过改装的大众帕萨特GTE上实现，如图1所示。接下来，我们将简要介绍关键硬件和软件组件。

2.1 研究车辆的硬件组件

在规划和实现车辆改装时，一个目标是使它们在硬件选型和视觉集成方面尽可能接近生产。原始

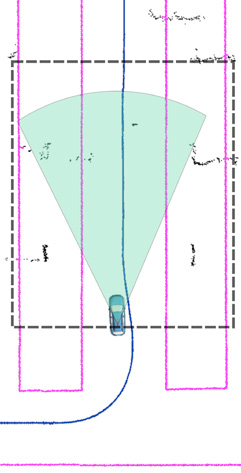
传感器系统由360◦个摄像头（区域视图）、超声波传感器（USS）、多功能摄像头（MFC）和雷达组成，并增加了两个 Ibeo ScaLa激光扫描仪。所有传感器的覆盖范围如图2所示。然而，由于项目持续时间较短，尚未考虑摄像头和雷达数据。此外，安装了一个民用全球导航卫星系统（GNSS）接收器，可计算支持实时动态定位（RTK）的位置估计，以及一个低成本惯性测量单元（IMU），用于提供车辆的加速度和转向速率。

安装了两台计算机（Spectra PowerBox）用于执行所有计算，同时使用加速度和方向盘转角值来控制车辆。控制信号通过大众驾驶员辅助系统原本使用的接口传输，该接口提供了额外的安全功能。此外，安全驾驶员可以在任何时候手动干预系统（纵向和横向）。

2.2 软件系统概述

提出的系统可分为三个主要模块：多传感器融合（FUS）、决策（DM）和控制（CTRL）。概览如图3所示。

FUS模块融合传感器数据，以估计车辆的当前状态并聚合关于其环境的信息。这些结果被DM用来决定车辆的行为，并在每个时间步长定义适当的目标状态。最后，CTRL基于非线性模型预测控制方法计算相应的控制命令。各个组件将在以下章节中讨论。

3. 多传感器融合

多传感器融合模块融合所有传感器数据，以实现车辆定位、创建环境地图以及检测车辆周围的障碍物。以下将分别描述这三个任务。

3.1 定位

定位的目标是基于绝对测量zt和相对状态转移测量ut来估计车辆的状态xt。后者包含IMU数据（加速度和偏航率）以及转向角，用于根据前一次的估计值xt−1预测状态xt。随后，使用包含GNSS位置估计和车辆报告的速度的zt，相对于绝对参考对xt进行校正。该状态的车辆由其位姿（位置和姿态）以及速度组成。此外，为了提供稳健的估计，还需要估计加速度计和陀螺仪的偏差。

因此，状态空间定义为 X:= R² × SO(2) × R × R × R = SE(2) × R³，其中SO(2) 表示二维旋转群，SE(2) 表示二维特殊欧几里得群。状态向量 xt ∈ X 为 xt := (r, ψ, v, δa, δω)，其中 r := (rx, ry) 为位置，ψ 为姿态，v 为速度，δa, δω 分别为加速度计偏差和陀螺仪偏差。

求解状态估计问题对应于计算在给定所有绝对测量值z₀:t和所有状态转移测量值u₁:t的情况下，状态xt的分布p(xt|z₀:t,u₁:t)。我们假设状态后验为均值µt ∈ X和协方差 Σt ∈ R⁶×⁶的正态分布，即状态服从分布式正态分布。

$$
x_t|z_{0:t}, u_{1:t} \sim N(\mu_t,\Sigma_t). \tag{1}
$$

因此，我们可以使用扩展卡尔曼滤波器（EKF）（Thrun 等，2005，第 3.3 节）来估计参数 µt,Σt。更准确地说，我们采用的是 Clemens 和 Schill (2016) 的实现方法，该方法基于所谓的 ‐方法¹（Hertzberg 等，2013）。这种形式化方法允许将流形状态空间如 X 无缝集成到传感器融合算法中。

¹ 发音为“boxplus方法”

3.2 地图

多传感器融合的建图子模块旨在提供对车辆环境的表示。具体而言，我们正在估计一种证据栅格地图（Pagac 等，1998），该地图基于置信函数理论（沙弗，1976；斯梅茨和肯尼斯，1994），可视为经典概率栅格地图（特伦等人，2005年，第9章）的推广。在此，每个网格单元 Yi ⊆ ΘY, 1 ≤ i ≤ M 是一个证据变量，用于指示相应区域是被占用（o）还是空闲（f）。因此，识别框架（即域中所有互斥可能性的集合）定义为 ΘY := {o, f}。此外，M 表示单元总数，完整地图由 Y ∈ Θᴹ_Y 给出。与概率栅格地图不同的是，证据栅格地图不仅可以将置信度质量分配给假设空间中的单元素集，还可以分配给所有子集，包括全集 ΘY 和空集 /0。通过这种方式，证据栅格地图能够表示并区分不确定性的不同维度（Reineking 和 Clemens，2014年）。

例如，知识缺失通过在 ΘY 上的质量来表示，而矛盾测量则导致在 /0 上的质量。在概率栅格地图中，这两者均通过均匀分布 P(o)=P(f)=0.5 表示，因此无法彼此区分不同的原因。证据栅格地图提供的额外信息可用于路径规划和探索任务（克莱门斯等人，2016）。

在创建地图时，我们采用已知位姿的地图构建方法（特伦等人，2005年，第9章），即使用第3.1节中讨论的算法来估计轨迹x₀:t，但在建图过程中忽略其不确定性。因此，我们的目标是估计在给定轨迹x₀:t和所有激光雷达测量值 ¯z₀:t的条件下，地图Y的条件质量函数m(Y|x₀:t, ¯z₀:t)。为了使计算可行，我们假设网格单元之间具有条件独立性，从而可以将所有网格单元的联合质量函数分解为边缘单元质量函数

$$
m(Y|x_{0:t},z_{0:t}) = \prod_{i=1}^{M} m(Y_i|x_{0:t}, \bar{z}_{0:t}). \tag{2}
$$

因此，地图更新可以应用于单个网格单元，而不是完整地图。特别是，每个网格单元的质量函数可以随时间递归地进行估计

$$
m(Y_i|x_{0:t}, \bar{z} {0:t}) = m(Y_i|x {0:t-1}, \bar{z}_{0:t-1}) ©∩ m(Y_i|x_t, \bar{z}_t), \tag{3}
$$

对于 1 ≤ i ≤ M。质量函数 m(Yi|x₀:t−1, ¯z₀:t−1) 对应于 t−1 时刻的地图置信度，而 m(Yi|xt, ¯zt) 是由当前测量 ¯zt 得到的地图置信度。后者是使用 Clemens 等 (2016) 提出的逆向传感器模型计算得到的。最后，算子 ©∩ 表示组合的合取规则（Smets, 1990）。与其他组合规则相比，©∩ 会产生在 ∅ 上的质量，从而能够识别冲突。由于车辆在停车场内的速度较低，连续的激光扫描具有较大的重叠区域。因此，地图不会对每次测量都进行更新，而仅在行驶过特定距离（例如 0.25 m）后才进行更新。

3.3 障碍物检测

上述讨论的证据栅格地图为较长时间尺度上的决策提供了基础。然而，由于它并非利用所有测量数据进行更新，因此对环境变化的适应速度较慢，因而仅部分适用于短期决策。为此，我们计算一个局部障碍物地图，以获取车辆周围障碍物的最新信息（见图4a）。此处使用概率网格地图，因为其已足以满足该目的。该地图中的每个网格单元 θi ∈ [0,1], 1 ≤ i ≤ N 表示在相应区域遇到障碍物的概率。完整地图由 θ ∈ [0,1]^N 给出，其中N表示单元总数，通常远小于证据栅格地图中的单元数量，即 N ≪ M。

与证据栅格地图不同，障碍物地图并非基于整个测量序列 ¯z₀:t 计算，而仅基于最新的测量值 ¯zₜ₋𝒹:ₜ 以及 d < t 进行计算。我们采用前向模型映射（Thrun 等, 2005年, 第9.4节）来解决建图问题，该方法使用前向传感器模型 p(¯zt|θi,xt) 而非逆向传感器模型 p(θi| xt, ¯zt)。该方法通过应用最大似然估计 (MLE) 来获得每个网格单元最可能的值 θ∗_i，从而得到结果

$$
\theta^* i = \arg\max {\theta_i \in [0,1]} \prod_{j=t-d}^{t} p(\bar{z}_t|\theta_i,x_t). \tag{4}
$$

通常情况下，该方程只能应用于整个轨迹片段 xₜ₋𝒹:ₜ 和整个测量片段 ¯zₜ₋𝒹:ₜ，即地图无法随时间递归地进行估计。然而，如果使用激光扫描仪等高精度传感器，(4)式可简化为 θ∗_i = ki / (ki + li)，其中 ki, li 是计数器，用于指示相应网格单元位于终点的次数

激光束以及未被激光束击中但被穿过的次数。因此，可以通过根据 ¯zₜ₋𝒹₋₁ 和 ¯zₜ 分别递减和递增计数器，从 ¯zₜ₋𝒹₋₁:ₜ₋₁ 的地图获得 ¯zₜ₋𝒹:ₜ 的地图，这使得算法非常高效。

4. 决策

决策模块负责决定自动驾驶汽车的行为。它将车辆状态及其环境的当前估计值与先验知识以及乘客输入相结合。在停车场探索过程中，先验知识涉及停车场的几何结构和各个停车位的大致位置，而乘客输入可能是感兴趣区域或在下一个可用停车位停车的指令。除了根据当前情况设置转向指示灯或定义合适的目标速度外，决策模块主要负责两项子任务：（a）评估融合传感器数据以识别可用停车位；（b）通过高频（例如50赫兹）定义期望目标状态，提供引导以确保车辆持续行驶。

4.1 停车位检测

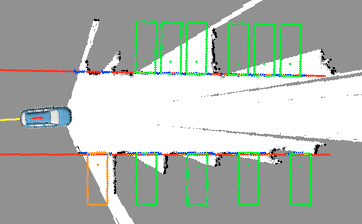
停车位基于障碍物地图进行检测（见第3.3节）。该过程如图4b所示，包含三个步骤。第一步旨在检测车辆左右两侧停放车辆的排布。我们假设其他车辆大致沿直线相互对齐。因此，为了检测面向我方车辆的边界，将障碍物地图结合每个网格单元相关的不确定性，变换到直线霍夫空间（杜达和哈特，1972年）。随后根据某些准则（例如相对于我方车辆的距离和角度）在每一侧选择一条直线（图4b中的红色线）。第二步中，我们沿着这两条线搜索空闲区域（图4b中的蓝色点）。在此过程中，不仅考虑恰好位于线上的网格单元，还考虑邻近的一些网格单元。第三步确定可能的泊车位姿。为此，我们将矩形拟合到第二步获得的空闲区域中（图4b中的绿色矩形）。每个矩形的尺寸与我方车辆尺寸相同（并加上安全裕度），且正交于第一步中检测到的直线。此外，代表我方车辆后部的边与对应的直线对齐。如果仅有一个矩形可放入一个停车位，则将其放置在该空间的中心位置（图4b底行）；如果有多个矩形可放入同一空间，则它们均匀分布（图4b顶行）。之后，选择其中一个矩形（例如最近的一个）作为初始停车姿态（图4b中的橙色矩形）。一旦车辆能够观测到整个停车位，便对其进行优化。

4.2 引导

引导子模块的任务是持续在预定义距离（例如15米）处定义新的期望目标状态x_T。为此，在初步步骤中会根据第5节中定义的最优控制问题，仅基于环境的先验知识，计算一次最优参考轨迹。之后，引导将尽可能地跟踪相应的位姿和姿态。

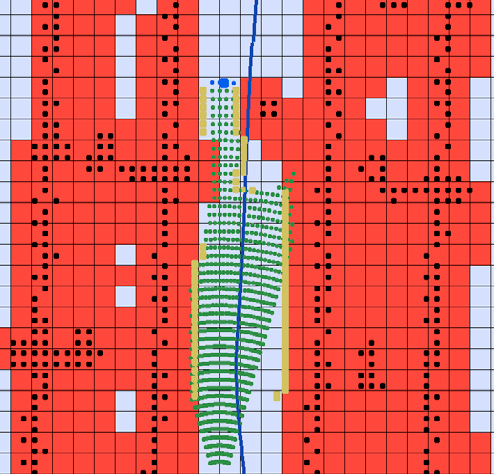
然而，由于其他车辆或行人的存在，参考轨迹可能会变得不可行，因此在每个时间步长都会通过高效的备用算法计算出一个替代目标状态。在此过程中，通过将环境估计结果转换为粗略障碍物网格（见图5b）来评估环境。从车辆的位置开始，沿当前行驶方向及其正交方向迭代搜索可行目标。如果该算法无法找到无障碍车道，则选择一个可行位置，使CTRL模块执行停车操作。在存在多个解的情况下，选择与参考轨迹偏差最小的结果。

连续计算得到的目标状态x_T通常彼此非常接近。然而，由于移动障碍物或切换到转弯或停车操作等情况，可能会出现较大的差异。在这种情况下，会对先前解和新解进行插值，从而使CTRL模块能够以前一步的结果作为初始猜测。

5. 非线性模型预测控制

为了将车辆从初始状态转移到由决策模块给出的期望目标状态，控制模块使用了一种非线性模型预测控制器（NMPC）。在此过程中，最优控制问题被持续地定义并求解。与常见控制方法相比，NMPC计算成本较高，但由于其考虑了非线性动力学和路径约束，因此具有显著优势（参见Paden等人，2016）。在汽车领域，(N)MPC已有一些应用，其中大多数展示了其在仿真中的适用性（参见Li等人，2017；Weiskircher等人，2017）。Falcone等人（2007）展示了基于MPC的控制方法在dSpace Autobox上的实现。

5.1 最优控制问题

每次操纵的规划均可视为对最优轨迹的搜索，因此可将其表述为一个最优控制问题。

$$
\begin{aligned}
\min_{x,u,T} &\quad J(x, u, T) \
\text{s.t.} &\quad \dot{x}(t) = f(x(t), u(t)), \
&\quad x_{\min} \leq x(t) \leq x_{\max}, \
&\quad u_{\min} \leq u(t) \leq u_{\max}, \
&\quad \Psi_1(x(0),x(T)) = 0, \
&\quad \Psi_2(x(0),x(T)) \leq 0, \
&\quad C(x(t), u(t),t) \leq 0 \quad \text{for all } t \in [0, T].
\end{aligned}
\tag{5}
$$

状态x、控制u以及过程时间T被确定为使得目标函数J最小化。(5) 的每个解都满足由f给出的动力学、由 Ψ₁和 Ψ₂提供的边界条件，以及其他路径约束，例如由函数C定义的避障。过程时间T可以是固定的或自由的。所有状态和控制分别受限于物理边界x_min,x_max和u_min,u_max。

为了求解形式为(5)的最优控制问题，我们采用直接法（Bates, 2010），并使用软件框架TransWORHP（Knauer和Büskens，2012）。该方法将无限维最优控制问题转化为一个非线性优化问题(NLP)，然后利用NLP求解器WORHP（Büskens和Wassel，2012）进行求解。

5.2 单轨模型

为了描述车辆的动态行为，采用了一种运动学单轨模型，该模型由于在停车场低速行驶且相应外力较小，具有足够的精度（Polack 等，2017）。在此方法中，每个轴上的车轮被替换为一个虚拟车轮。所得模型描述了后轮的x‐y位置、车辆相对于参考坐标系的姿态 ψ、转向角 β、速度 v以及加速度a。为了确保控制信号的连续和平滑，我们在模型中加入了加速度和转向角的导数。因此，将转向角速度ωβ作为额外的状态变量，控制量则由急动度j和转向角加速度aβ组成。结合轴距L，这导致了

$$
\begin{aligned}
\dot{r} x &= v \cdot \cos(\psi), & \dot{\psi} &= \frac{v \cdot \tan(\beta)}{L}, \
\dot{r}_y &= v \cdot \sin(\psi), & \dot{\beta} &= \omega \beta, \
\dot{v} &= a, & \dot{\omega} \beta &= a \beta, \
\dot{a} &= j.
\end{aligned}
\tag{6}
$$

定义状态 $ x := (r_x, r_y, \psi, v, \beta, \omega_\beta, a)^\top \in \mathbb{R}^7 $ 和控制量 $ u := (j, a_\beta)^\top \in \mathbb{R}^2 $，系统(6)对(5)中的动力学f进行建模。由于物理限制以及平顺驾驶的舒适性要求（Sommer 等，2018），状态和控制量分别受限于 $ x_{\min}, x_{\max} \in \mathbb{R}^7 $ 和 $ u_{\min}, u_{\max} \in \mathbb{R}^2 $。

5.3 边界条件与障碍物避让

(5)中的初始状态x(0) 应与x_est相对应，该值由当前状态估计x_t （见第3.1节）以及额外的值（例如来自前一次优化步骤的值）组成。此外，要求x(T)位于决策模块DM确定的目标状态x_T的邻域内（见第4.2节）。当ε ∈ ℝ⁷≥₀较小时，并结合按分量取绝对值的运算符 | · |，这些条件可通过(5)中的Ψ₁和 Ψ₂表示为

$$
\Psi_1(x(0),x(T)) := x_{\text{est}} - x(0), \quad \Psi_2(x(0),x(T)) := |x_T - x(T)| - \varepsilon.
\tag{7}
$$

为了防止车辆与障碍物发生碰撞，函数C迫使式(5)的解与障碍物地图中的所有障碍物保持最小安全距离（参见第3.3节）。为此，通过闭合多边形链定义一个可通行区域，同时用车辆自身的重叠圆近似表示车辆（Sommer 等，2018）。

5.4 目标函数

目标函数包含过程时间、控制量、选定状态以及依赖于决策模块DM提供的目标状态x_T的惩罚项的加权组合。此外，还加入了与决策模块DM确定的期望速度v_set的平方偏差。这得到

$$
\begin{aligned}
J(x, u, T) := &\ w_0 T + \int_0^T \left( w_1 \omega_\beta^2 + w_2 a^2 + w_3 j^2 + w_4 a_\beta^2 \right) dt \
&+ \int_0^T w_5 (v - v_{\text{set}})^2 dt \
&+ w_6 (r_x(T) - r_{x,T})^2 + w_7 (r_y(T) - r_{y,T})^2 \
&+ w_8 (\psi(T) - \psi_T)^2 + w_9 (\beta(T) - \beta_T)^2.
\end{aligned}
\tag{8}
$$

在探索过程中，w₆,…,w₉被设为零，且(7)中的Ψ₂应成立。当进入停车位时，w₆,…,w₉ > 0被设定，而Ψ₂被忽略。权重可根据当前应用、情况和环境进行自适应调整。

5.5 实现

建立形式为(5)的最优控制问题，结合(6)、(7)、(8)及物理约束（Sommer 等，2018）。一旦求解(5)，前几个控制信号（加速度和方向盘转角，参见第2.1节）即被传输至车辆。因此，所确定的转向角 β被转换为方向盘转角。随后，使用新的当前估计状态重新建立(5)并再次求解。

即使非线性模型预测控制（NMPC）能够适应变化的环境，仍可能存在需要车辆迅速停止的情况。为了确保立即响应，使用一个高优先级的安全模块（safety module）来启动紧急制动操作。该模块会监测并评估车辆行驶方向上与障碍物的最小距离，同时考虑当前车速和转向角。如果存在潜在碰撞风险，该模块将覆盖由非线性模型预测控制确定的加速度值，并使车辆停止。

6. 实际演示

为了展示所提出的自动驾驶系统，我们展示了在不来梅大学停车场进行探索的结果。我们展示了自动驾驶车辆如何通过执行车道保持、动态考虑障碍物，最终完成泊车操作来探索该区域。选取了两条走廊作为感兴趣区域，并提供了一组停车位，车辆需要从中找到一个空闲车位。

图6展示了第3.2节中描述的不断更新的证据栅格地图。在探索过程中检测到的停放车辆和其他障碍物被相应地记录下来。利用FUS提供的信息以及停车场的先验知识，决策模块为控制确定期望目标状态。图7展示了一个示例情况，其中车辆被引导完成左转。需要注意的是，图7b中的后验位姿与图7a中所示路径略有偏差，因为决策模块会持续定义新的目标状态，且所使用的模型仅为实际情况的近似。

当发现空闲停车位时，由决策模块（DM）启动进入停车位的操纵。在此过程中，如第4.2节所述，期望的目标位姿被移至停车位内。Sommer等人（2018）展示了示例停车轨迹和操纵过程。

7. 结论

本文介绍了一种用于自主车辆导航与控制的系统，该系统是在AO‐Car研究项目中开发的。该项目的目标是在短短一年时间内，将为深空任务所开发的多传感器融合与非线性模型预测控制理论和方法应用于这一地面应用。在真实车辆上的实车测试表明，这些方法能够实现一个可在停车场环境中应对未知障碍物并自主探索停车场的系统。此外，系统还能检测空闲停车位，并可根据请求启动泊车操作。

总体而言，我们的结果表明，源自空间应用的方法可以以较低的成本和较高的成功率转移到自动驾驶这一地面应用中。所提出方法的一个主要优势是其通用性，可扩展至更多场景。目前，我们正在OPA3L项目中继续开展相关工作，该项目聚焦于城市交通，面临处理高度动态环境以及与其他车辆协作的挑战。另一个研究方向是对所提出的算法进行定量评估。