常数轮可重置零知识论证

常数轮次下的可重置安全的可重置零知识

摘要

在2001年FOCS上，巴拉克等人推测存在一种零知识论证，能够抵御可重置证明者和可重置验证者的攻击。邓等人在2009年FOCS上在多种复杂性假设下证明了该猜想成立，但需要多项式轮数。随后，钟等人在2013年FOCS上改进了该结果，仅需单向函数这一假设，但仍要求多项式轮数。

在本研究中，我们提出了一种constant-round具有可重置安全性的可重置零知识论证系统，从而将轮数复杂度从多项式降低至常数。我们通过以下步骤实现这一结果。

1. 我们展示了一种从任意 轮并发零知识论证系统到 O() 轮可重置零知识论证系统的显式变换。该变换基于巴拉克等人在 2001年FOCS 上以及邓等人在 2009年FOCS 上提出的技术。接着，我们利用了钟等人在 2015年CRYPTO 上提出的最新突破，该突破解决了在合理多项式时间硬度假设下构建常数轮并发零知识论证系统这一长期开放的问题。以他们的构造 Γ 为基础，我们得到了一个常数轮可重置零知识论证系统 Λ。
2. 接着，我们展示了通过将 Λ 巧妙地嵌入 Γ 中（即本质上是将钟等人的构造与钟等人的构造进行某种修改后的对抗），我们获得了首个常数轮具有可重置安全性的并发零知识论证系统 Δ。
3. 最后，我们应用了邓等人提出的一种变换到 Δ，从而得到一个具有可重置安全性的可重置零知识论证系统 Π，这是本工作的主要成果。

虽然我们为可重置零知识设计的保轮变换仅需单向函数，但 Λ,Δ和 Π扩展了钟等人的工作，因此它们依赖于相同的假设（即抗碰撞性哈希函数族、单向置换以及具有略微超多项式安全性的 P/poly的iO（不可区分性混淆））。

1 引言

私有随机性对于许多密码学任务至关重要，包括零知识（ZK）证明[24]。一个自然的问题是，在计算设备无状态且不具备持续随机性来源的应用中，是否可能实现零知识证明。

可重置零知识

上述问题由 Canetti 等人提出 [8]。具体而言，他们考虑了一种进行重置攻击的恶意验证者，其中证明者被迫多次执行协议，可能使用相同的输入和随机带，并且在执行之间无法维持状态。这些攻击包括无状态证明者的情况，以及通过可物理恢复到原始状态的设备实现的证明者（例如，通过克隆、更换电池）。

更具体地说，在[8], Canetti等人引入了可重置零知识（rZK）的概念，其中即使面对能够将证明者重置到初始状态、从而迫使其以相同随机性重复执行的作弊验证者，零知识性质也必须成立。这一概念与Dwork等人早先提出并发零知识（cZK）密切相关，后者中，作弊验证者可以参与多个可能交错的并发执行过程（称为会话）该协议。由于通过特定的重置策略，一个可重置的作弊验证者可以模拟交错的并发执行，因此实现rZK至少与实现cZK一样困难。在 [21] Garg等人表明，对于若干有趣的语言，可重置统计零知识是可行的。

cZK和 rZK的轮数复杂度

在看似成立的困难性假设下，常数轮 cZK 长期以来一直是一个具有挑战性的开放性问题，钟等人 [11]通过不可区分性混淆（iO） [11]对此给出了肯定的回答。相反，rZK 的情况更差。Canetti 等人在 [8] 中基于标准密码学假设在标准模型中构造了 rZK 证明，但其具有多项式轮复杂度1。轮数复杂度随后在[29]中被改进为准对数级。当前情况留下了以下开放问题。

开放问题 1 ：是否存在具有亚对数轮次的 rZK构造？

可重置安全性零知识

巴拉克等人[3]研究了这种自然的对立场景，称为可重置可 靠零知识（rsZK）论证，其中即使面对能够重置验证者的作弊证明者，可靠性也必 须成立，这些作弊证明者可迫使验证者重复使用相同的随机带。标准的零知识性质 保持不变。他们展示了在假设存在抗碰撞性哈希函数的情况下，该方案的常数轮构 造。最近的研究工作[12]达到了最优的轮数复杂度和假设条件（即4轮和单向函数）。

1此外，他们基于裸公钥提出了一种温和的设置假设，表明这对于常数轮可重置零知识 是充分的。后续工作优化了在裸公钥下rZK的轮数复杂度和复杂性假设[16,17,31,34,35]。

同时可重置性猜想

巴拉克等人在[3]中猜想存在一种零知识论证，能够同 时抵御可重置验证者和可重置证明者的攻击：即可靠可重置的零知识论证系统。该猜想被邓等人[15]证实成立，他们提出了一个基于碰撞抵抗哈希函数和陷门 置换假设下具有多项式轮数的构造方案。尽管计算假设已改进为单向函数 [4,5,13,14,33],，但多项式轮复杂度的障碍至今仍未被突破。

开放问题 2 ：是否存在具有亚多项式轮数的可重置可靠 rZK构造？

我们强调，通过将针对可重置验证者的安全性要求从零知识放宽为见证不 可区分性，便可以实现常数轮次的同时可重置性。事实上，仅需1或2轮次（即 ZAPs）即可获得证明，而只需更多一点的常数轮次即可获得知识论证 [9]。

1.1 我们的结果

在本文中，我们对上述问题给出了肯定的回答。我们的主要成果是为 N P构建 了一个常数轮同时可重置零知识论证。我们的结果依赖于抗碰撞性哈希函数族、 单向置换以及具有略微超多项式安全性的P/poly的不可区分性混淆（iO）的 存在性。这些假设与[11]中展示的用于 N P的常数轮并发零知识论证所采用的假 设相同。我们的结果以某种嵌套方式两次使用了[11]的协议。更准确地说，第 一次我们使用[11] Γ的协议是为了获得一个常数轮rZK论证 Λ。然后我们再次 从 Γ出发，并通过在相反方向使用 Λ（即 Γ的一个修改版本）作为子协议（即验证者将向证明者证明某些内容）对其进行修改。因此，我们大致上将[11] 的协议用于对抗[11]的协议，这一点颇为有趣。这种对[11]协议的嵌套使用使 我们能够获得一个常数轮的可重置可靠并发零知识论证 Δ。随后，我们可以应 用[15]提出的一个编译器到Δ，从而得到我们的主论证系统Π，该系统在仅需 常数轮次的情况下，同时对可重置证明者和可重置验证者均具备安全性。

我们现在给出正式的定理，以明确指定具体的复杂性假设。

定理1 。 假设单向函数存在，那么任何 轮并发零知识论证系统都可以被转换 为一个 O()轮可重置零知识论证系统。

定理2 。 假设存在抗碰撞哈希函数、单向置换以及针对 P/poly的不可区分混 淆（具有略微超多项式安全性），则存在一个常数轮可重置可靠性的可重置零 知识论证系统，用于 N P。

1.2 主要工具与我们的新技术

我们的构造依赖于新思想，以及对以往关于并发、可重置和可重置安全性零知 识结果中所使用多种技术的综合运用。我们首先简要描述在构造过程中所使用 的重要工具，以及我们引入的新技术。

Barak的非黑盒协议

起点是巴拉克针对 N P[1]的非黑盒零知识论证，其工作 方式如下：证明者 P向验证者 V发送一个值为0的承诺 c ∈{0, 1}n；然后验 证者 V发送一个均匀生成的随机字符串 r ∈{0, 1}2n；最后，证明者给出一个 不可区分见证的通用论证（WIUA），以证明 x ∈ L成立，或者存在 σ ∈{0, 1}n使得 c是对某个程序 M的承诺，且满足M(σ) = r2。该协议的 可靠性来源于承诺方案的绑定性和WIUA的可靠性，因为任何由作弊证明者所 承诺的程序 M，在其支持集中不包含 r的概率极高。对于零知识性质，模拟 器会使用攻击者的代码，具体而言，它会承诺一个对应于作弊验证者 V ∗代码的 程序 M。令 σ为该承诺，则有 M(σ) = r2，并且 σ相较于 r较短。

钟等人的常数轮 cZK论证

在[11],钟等人 构造了一种常数轮 cZK论证， 该论证使用具有可委托的CRS生成的唯一 P‐证书系统 [10]和 iO。非正式地 说，一个 P‐证书系统允许一个高效的证明者使用固定（多项式）长度的证书来 向验证者证明任何确定性多项式时间计算 M(x) = y的有效性，且该证书的长 度与 M 的大小和运行时间无关。验证者也可以在固定的（多项式）时间内验 证该证书，且验证时间与 M 的运行时间无关。在一个具有可委托的CRS生成 的 P‐证书系统中，证书是使用公共参考串（CRS）生成的，而该CRS可以由验 证者委托的资源来计算。更具体地说，在这个 P‐证书系统中， P‐证书验证者 生成公共参数和私有参数，即 PP 和 κ，并将 PP 发送给 P‐证书证明者。 P‐ 证书证明者使用公共参数 PP 和语句 q=(M, x, y) 来确定性地计算一个短摘 要 d，其长度与 q的长度无关，并将该摘要发送给 P‐证书验证者。然后， P‐ 证书验证者使用 d 和 κ 计算出 CRS。最后， P‐证书证明者利用 CRS 和 q 计算出证书。如果对于任意语句和 CRS 至多存在一个被接受的证书，则该 P‐证 书系统是唯一的。

[11]的论证过程与巴拉克的论证类似，但有以下修改。在最后一步中，不再要求证 明者 P进行证明

2由于 M的大小可能无法预先确定，因此承诺是对程序 M的哈希值，该哈希值使用在 协议开始时由验证者选择的一组抗碰撞性哈希函数中的哈希函数 h计算得到。其可靠性 也基于 h的抗碰撞性。

x ∈ L或者存在 σ使得 c是对一个程序 M的承诺，且满足 M(σ) = r，此时证 明者提供一个特殊可靠性的无见证识别性证明，以证明 x ∈ L或者存在一个 P‐ 证书 π，该证书验证了 M(σ) = r对某个短字符串 σ成立。此外， P还进行承 诺，并提供一个WIUA证明，表明在从 V接收到公共参数 PP之前，要么 x ∈ L成立，要么存在一个针对语句 q=(M, σ, r)的 P‐证书。注意，由于在 [11]中的协议的诚实证明者拥有 x ∈ L的一个见证，因此它可以忽略CRS、d 和 q，只需承诺为零即可。为了使零知识模拟器（注意诚实证明者将直接使用 x ∈ L的见证）能够从 d和 κ计算出CRS，验证者发送一个内部嵌入了 κ的混 淆程序，使得模拟器可以从之前承诺的 d计算出CRS。最后， V还提供一个零 知识论证，以证明该混淆程序被正确计算。

模拟器不知道 x ∈ L的证人，而是能够承诺攻击者的代码。更正式地说， 模拟器分为两部分： S1，其在第 i轮接收 P‐证书 πi作为输入，并与验证者 V ∗ 进行交互；以及 S2 ，其在第 i轮提供P‐证书，证明 S1在输入(1, π1)…,( i − 1, πi−1)时输出 mi。模拟器 S=(S1, S2)并非使用验证者 V ∗的代码来承诺一个程 序 M，使得M(σ)= r对于某个短字符串 σ成立，而是承诺一个˜程序 S1。该 程序在输入(1n, j, s)时，以 s为种子生成伪随机硬币，并通过访问提供 P‐证书 的预言机 OVcert，在 j轮次内运行 S1和 V ∗之间的交互。这避免了并发会话的 嵌套，从而防止因 S中生成 P‐证书这一昂贵步骤导致运行时间急剧增加。因 此，[11]中协议的模拟器要么能在关于语句 x ∈ L的特殊可靠证人不可区分性 证明中成功，要么存在一个 P‐证书 π，利用预言机的输出作为证人，证明 S˜OV cert 1 (1n, j, s)= r对某个短字符串(1n, j, s)成立。

邓、戈亚尔和萨哈伊的变换

在[15,25],邓等人构造了一个混合可重置安全且宽 松并发零知识论证ΠDGS。然后他们应用一系列变换以实现同时可重置性。

宽松并发零知识允许验证者在多个会话中与独立的证明者进行交互。然而， 零知识性质仅针对“宽松”的并发验证者提供保证，这些验证者的随机硬币在 每个会话开始时即被固定，且独立于在此之后开始的其他会话。请注意，任何 并发零知识论证/证明也同样是宽松并发零知识的，因为任何宽松并发验证者也 是一种并发验证者。

混合可重置可靠性意味着验证者可以被分为两个部分， V1和 V2。 V1直 接与 P交互，可以在 P和 V2之间转发一些消息，并且可以被作弊证明者重置。 V2仅与V1交互，不能被作弊证明者重置，并负责决定是“接受”还是“拒绝” 该论证。此外，对于每个determining message（决定性消息）

第一条消息 V2在协议中接收到的）， P无法找到两条不同的消息，使得 P能 够说服 V1传递给 V2在每一轮中。有关精确定义，请参见[25]。注意，任何可 重置可靠论证都可以通过以下方式成为混合可重置可靠：让 V1表现得如同 V 一样，只是不再接受该论证，而是向 V2发送一条消息，且 V2在收到来自 V1的 消息时总是接受该论证。

邓等人的变换使用ZAPs和单向函数来实现同时可重置性，且仅将轮数复杂 度增加一个常数因子。然而， ΠDGS的轮数复杂度是多项式级[15]。因此，他 们的同时可重置论证系统也需要多项式轮次。

变换的不可适用性[15]于钟等人的构造[11]

直观上，人们可能会尝试将 [15]的变换应用于[11]中的常数轮并发零知识论证，以获得同时可重置性。然 而，为了使变换后的结果是同时可重置的，要求起始协议是宽松并发零知识且 混合可重置可靠的。尽管[11]中的协议是并发零知识的，这意味着它也是宽松 并发零知识的，但我们认为，如果（不可重置）ZK论证（用于证明混淆程序被 正确计算）对重置的验证者而言不是零知识的，则该协议无法被证明为混合可 重置可靠。原因如下两点。

1. 假设在极端情况下，存在一个对抗性重置证明者，该证明者针对[11]的论证 运行了一个重置攻击者 AZK，在（不可重置）零知识子协议中，诚实的验证 者需证明混淆程序被正确计算。请注意，该零知识子协议也可能是一种知识论 证，允许使用黑盒（回卷）提取器。通过成功运行 AZK，该对抗性重置证明者 可能提取到某些相关信息（例如，用于 P‐certificate CRS生成的秘密参数， 该参数在验证者向证明者证明的（不可重置）ZK论证中被用来保证混淆程序的 正确性）。然而，根据混合可重置可靠性的定义，我们需要考虑验证者 V= 的两个独立部分(V1, V2)。其中 V1和 V2之一将作为ZK论证的证明者，以证明 混淆程序被正确生成。如果（不可重置）ZK论证由 V1（作为证明者）执行， 而该证明者可以被重置，则[11]中的恶意证明者可以运行 AZK来获取某些相 关信息（例如，秘密参数），这可能会被用来为一个虚假语句生成证书。另一 方面，如果（不可重置）ZK论证由 V2（作为证明者）执行，那么由于该论证 中验证者的消息并未由[11],协议中的确定性消息固定，因此 V2可能对同一个 确定性消息接收到两个不同的消息，因此即使在这种情况下，该协议也不是混 合可重置可靠的。
2. [11]协议中的 P‐证书生成无法使用[3]的技术转化为可重置可靠协议。这是因为 the P‐证书系统不是公开硬币系统。回顾在[3]中对可重置可靠性的证明， 该证明通过反证法从一个（成功的）可重置证明者出发，将其归约为不可重 置情形。如果我们在此重复相同的归约，则不可重置证明者会通过自身模拟 验证者来运行除一个会话外的所有会话。当然，这要求能够在重置攻击下生 成合法的验证者消息。当尝试发送合法验证者消息时，不可重置证明者可能 会向可重置证明者发送归约中真实验证者的混淆程序，而可重置证明者可能 会重置到其接收到 P‐证书的公共参数之后的步骤。在这种情况下，不可重 置证明者将无法在不知道秘密参数的情况下按照协议规定生成新的混淆程序。

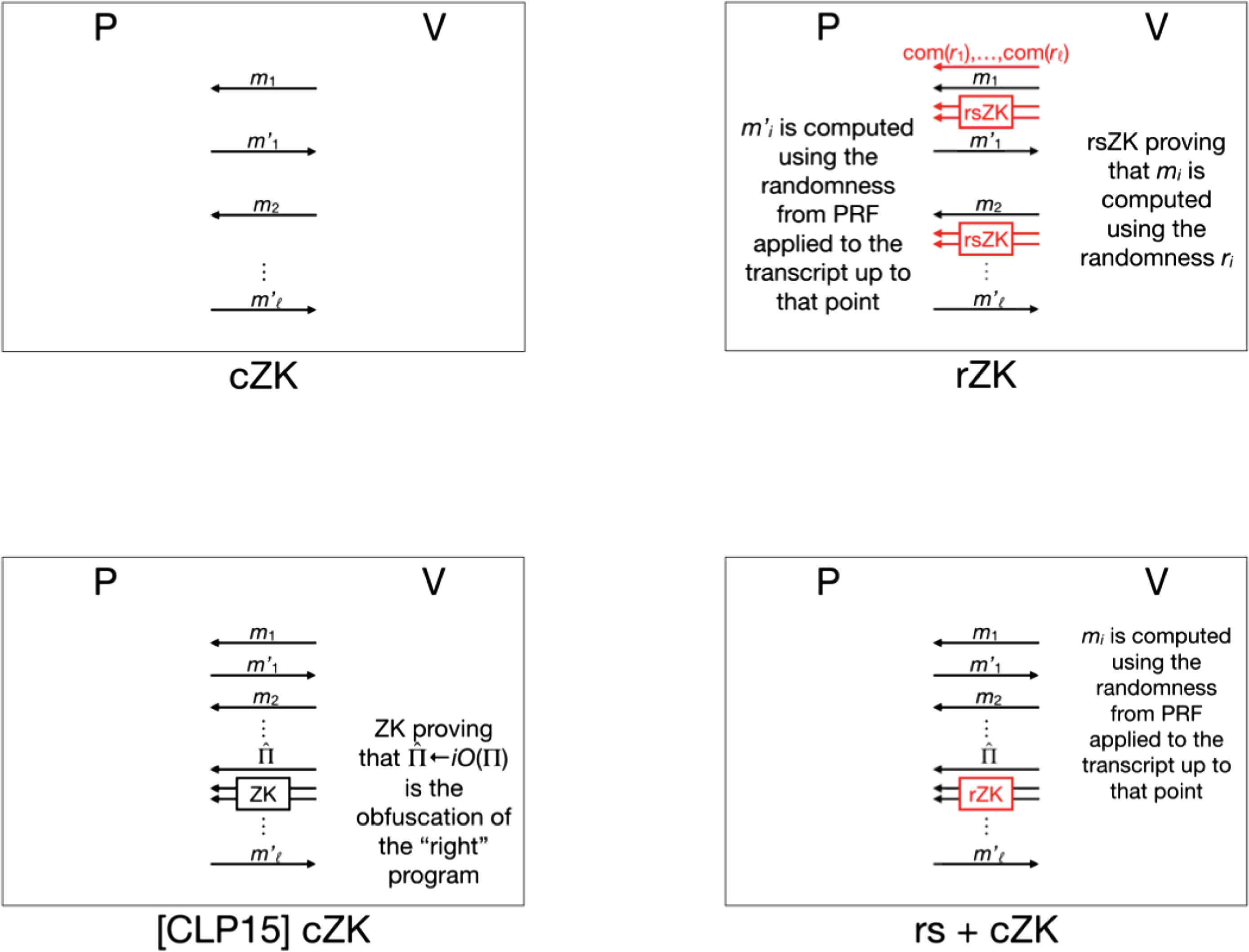
1.3 我们的方法

为了获得常数轮可重置可靠并发零知识论证系统，我们考虑来自[11]的协议， 该协议是常轮次且并发零知识的，但不具备可重置可靠性。如上所述，

有两个主要问题使得[11]的协议无法达到可重置可靠性：即针对 iO的不可重 置的零知识论证，以及 P‐证书系统的可委托CRS生成机制，该机制无法在不知 道前一步骤中生成的秘密参数的情况下完成生成。

解决第一个问题

我们通过从[11]的并发零知识论证构造一个常数轮数的可重置零知识论证来解决第一个问题。该变换在之前一些相关工作中已有隐含体现 [3,15]。我们在此明确地给出这一变换以确保完整性（图1）。

与并发验证者不同，可重置验证者可以在重置攻击期间通过重复使用随机 带来发送不同的消息，从而从证明者处提取额外信息。我们通过以下两点来防 止此类行为：（1）要求验证者使用统计绑定承诺方案对其随机带进行承诺； （2）提供一个零知识论证以证明其确实使用了已承诺的随机带。需要注意的是， 由于验证者可以重置证明者，因此不具有可重置可靠性的零知识论证无法被验 证者用来证明其使用了已承诺的随机比特。因此，该论证系统必须具备可重置 可靠性。为了保持轮数复杂度，此子协议必须是常数轮的。这可以通过钟等人 提出的4轮可重置可靠的零知识论证[12]来实现。类似的技术已在[26]中用于可 重置安全计算。

我们注意到，常数轮 rsZK 论证和承诺方案可以基于单向函数构建，而 [11] 中的常数轮并发零知识论证也假设了单向函数的存在。因此，对该协议应用此 转换不需要额外的假设。事实上，我们所使用的技术可以推广为一个适用于任 何并发 ZK 协议的编译器。所得协议的轮数复杂度仅增加一个常数因子。

我们的编译器将任何并发零知识论证转换为可重置零知识论证的工作方式 如下。首先，我们将证明者用于生成其消息的随机硬币替换为PRF的输出。这 一步骤使得具有固定随机带的证明者能够在可重置验证者重置后更改其消息时 发送不同的消息，类似于[3]中用于对抗可重置证明者的技术。此外，验证者在 协议开始时对其每一轮使用的随机硬币进行承诺。在发送每条消息之后，验证 者提供一个常数轮可重置可靠零知识论证，以证明其使用了第一轮中已承诺的 随机硬币。此修改确保验证者在每个会话中都遵循协议。

解决第二个问题

为了解决第二个问题，我们注意到，尽管[11]的协议不是公 开硬币的，但它是“几乎公开硬币”的。所谓几乎公开硬币，是指除了上述被 rZK论证替换的零知识论证外，验证者仅有一条消息不能作为公开硬币独立生 成，而是依赖于隐藏的随机性。因此，我们修改[3]中的技术，通过以下两个步 骤来解决该问题（图1）。

首先，我们考虑[11],协议的一个修改版本，在该版本中我们可以证明其 （不可重置）可靠性。在此协议中，来自 V的消息无法用均匀随机硬币生成的 轮次被重复m次，其中 m= poly(n) 是作弊证明者 P∗运行时间的上界。更具 体地说，在收到P‐证书的公共参数后，修改后协议的证明者 PS反复对他的语 句摘要进行承诺并证明其有效性，而验证者 VS则反复回复用于验证被承诺值的 混淆程序，并输出 P‐证书的CRS。 PS随后选择哪一对承诺和混淆程序将用于 完成协议。由于 iO的安全性， PS即使经过 m次重复，也无法获知 P‐证书的 秘密参数。因此，所得协议仍然是可靠的。

然后，我们将最终协议的可重置可靠性规约到上述协议的不可重置可靠性， 该规约在成功概率上为多项式规约，具体如下。给定一个可重置证明者 P∗， 我们通过在内部模拟 P∗ 与验证者 V 的交互，并随机选择哪一次 m 重复将 产生接受 transcript，从而构造出一个不可重置证明者 P∗ S。对于其他重复， P∗ S 将自行生成 P‐certificate 的参数，以应对非公共硬币情况。当 P∗ S 正确 猜中接受 transcript 时（发生的概率为 1/m），它将从模拟中获得该接受 transcript 并成功说服验证者 VS。

1.4 开放性问题

与上述从并发零知识到可重置零知识的编译器不同，我们对可靠可重置零知识 的构造以非黑盒方式使用了[11]的协议。

我们的工作留下了两个自然的问题：一是如何构建一种通用的、保持轮数 的从cZK到rZK的转换方法，二是在更标准的复杂性假设下实现常数轮的可重 置可靠可重置零知识。

2 定义

一个多项式时间关系 R 是指可以在关于 |x| 的多项式时间内验证 R(x, w) = 1 的关系。考虑一个 N P‐语言 L，记 RL 为相应的多项式时间关系，使得 x ∈ L 当且仅当存在 w 使得 RL(x, w) = 1。我们将这样的 w 称为 x ∈ L 的 有效证人。令 λ 表示安全参数。可忽略函数 ν(λ) 是一个非负函数，满足对于 任意常数 c< 0 和所有足够大的 λ，均有 ν(λ)< λc。我们用 Prr[X] 表示事 件 X 在随机硬币 r 上的概率，当 r 未指定时简记为 Pr[X]。“PPT” 是概 率多项式时间（probabilistic polynomial time）的缩写。对于一个随机化算 法 A，令 A(x; r) 表示在输入 x 上以随机硬币 r 运行 A。如果 r 被均匀随 机选取并输出 y，我们记作 y ← A(x)。对于一对交互式图灵机

(P, V)，令 〈P, V〉(x)表示 V在以公共输入 x与 P交互后的输出。如果 〈P, V〉(x) = 1，我们称 V接受；如果 〈P, V〉(x) = 0，则称其拒绝。我们用viewP(w) V x z( , )表 示 V在以公共输入 x和辅助输入z与 P(w)交互过程中所产生的视图（即其私有随 机硬币和接收到的消息）。我们将采用标准的计算不可区分性[23]概念。

我们现在给出对交互式证明/论证系统及其所有在此工作中有用的变体的定义。

定义1 (交互式证明 [24])

对于语言 L的交互式证明系统，是由一对在公共输 入 x上运行的交互式图灵机(P, V)构成的，满足以下条件： –效率： P和 V是 PPT。–完备性：对于每个 λ∈N以及每一对(x, w)，使 得 RL(x, w)=1， Pr[〈P(w), V〉(1λ, x)= 1]= 1. –可靠性3：存在一个可忽略函数 ν(·)，使得对于每一对交互式图灵机(P∗ 1, P∗ 2) Pr[(x, z) ← P∗ 1(1λ): x∈/ L ∧〈P∗ 2, V〉(1λ, x)= 1]< ν(λ). 在上述定义中，我们可以将可靠性要求放宽，即将P ∗视为PPT。在这种情况下， 我们称(P, V)是一个交互式论证系统[7]。

定义2 (零知识论证 [24])

设(P, V)是语言 L的一个交互式论证系统。我们称 (P, V)具有零知识性（ ZK），如果对于任意概率多项式时间攻击者 V ∗，存在 一个概率多项式时间算法 SV ∗，使得对于所有辅助输入 z和所有对(x, w) ∈ RL，集合{view P(w) V ∗ x(,z)}和{SV ∗(x, z)}是计算上不可区分的。

假设(P, V)被用作另一个交互协议(A1, A2)的子协议，其中 A1运行 P， A2 运行 V。我们称图灵机 A1 α为残余证明者，如果 A1 α在 A1调用 P时，使用来自 A2的输入 α=(α1,…, α)运行 A1，直到并包括第 轮。类似地，通过交换 A1 和 A2可定义残余验证者 A2 α。注意，在模拟V（用于可靠性）时会调用残余证 明者，而在模拟 P（用于零知识性）时会调用残余验证者。

定义3（重置攻击者 [8]）

设(P, V)是针对语言 L, t= poly(λ), x¯= x1,…, xt的一个交互 式证明或论证系统，其中 w¯= w 1,…, w t是相应的公共输入序列，{v25},…,{v26}是相应 的证人（即(xi, w i) ∈RL）对于 i= 1,…, t。令 r 1,…, r t为独立随机带。我们说

3此版本的可靠性由 [11]给出，与标准版本中单一图灵机的版本略有不同 P ∗。将它们 分开使得证明更加清晰，同时仍等价于标准版本。

一个PPT V ∗是一个重置 验证者，如果它通过为每次交互选择值i ，使得公共 输入为 xi ∈ x¯，证明者使用 wi作为证人，并选择 j使得证明者使用 rj作 为随机性，且 i, j ∈{1,…, t}，从而与无限数量的 P的独立副本来并发交互。 此外，不同交互中与 P的调度或要发送的消息由 V ∗自由决定。此外，我们说此 类交互的交互记录包括公共输入 x¯以及交互过程中交换的证明者和验证者消息 序列。我们将 viewP(w¯)V ∗(x¯,z)称为描述 V ∗的随机带内容以及 P和 V ∗之 间交互记录的随机变量，其中 z是 V ∗收到的辅助输入。

定义4（可重置零知识 [8]）

设(P, V)是语言 L的一个交互式论证系统。我 们称(P, V)为可重置零知识（rZK），如果对于任意 PPT可重置验证者 V ∗， 存在一个期望概率多项式时间算法 SV ∗，使得对于所有对(x¯, w¯) ∈ RL，集合{ viewP(w¯)V ∗(x¯,z)}和{SV ∗(x¯, z)}是计算上不可区分的。

并发零知识的定义可以被视为对可重置零知识定义的一种放松。对抗性的 并发验证者与可重置验证者具有相同的能力，只是它不能要求证明者以相同的 随机性运行多个会话。

定义5（并发攻击者）

设(P, V)是语言 L的一个交互式证明或论证系统， t=poly(λ), x¯= x1,…, xt是一个公共输入序列， w¯= w1,…, wt是相应 的证人（即(xi, wi) ∈ RL）对于 i= 1,…, t。我们称一个 PPT V ∗为并发验 证者，如果它通过为每次交互选择值 i ，使得公共输入为 xi ∈ x¯，且证明者使 用证人 wi，从而与 P的无界数量的独立副本进行并发交互。每个 P的副本 使用独立的随机性运行。与 P在不同交互中的调度或要发送的消息由 V ∗自 由决定。此外，我们说此类交互的交互记录包含公共输入 x¯以及交互过程中交 换的证明者和验证者消息序列。我们将 viewP(w¯) V ∗(x¯,z)称为描述 V ∗的随机带 内容以及 P和 V ∗之间交互的交互记录的随机变量，其中 z是 V ∗收到的辅 助输入。

定义6 (并发零知识 [19])

设(P, V)是语言 L的一个交互式论证系统。我们 称(P, V)为并发零知识（cZK），如果对于任意 PPT并发验证者 V ∗ ，存在一 个概率多项式时间算法 SV ∗，使得对于所有对(x¯, w¯)∈ RL，集合{viewP(w¯)V ∗ (x¯,z)}和{SV ∗(x¯, z)}是计算上不可区分的。

定义7（见证不可区分性 [20]）

设 L为 N P中的一个语言，RL为其对应的对应关 系。一个交互式论证(P, V)对于 L是

witness indistinguishable（WI），如果对于每个验证者 V ∗ ，每一对(w0, w1)满足(x, w0) ∈ RL且(x, w1) ∈ RL，以及每个辅助输入 z，以下集合是计算上不可区分的： {viewP(w0) V ∗(x,z)} and{viewP(w1) V ∗(x,z)}.

定义 8（可重置 WI[8]）

设 L是 NP中的一个语言，RL是其对应关系。 对于 L的交互式论证(P, V)，如果对于每一个 PPT可重置验证者 V ∗ 、每一 个 t= poly(λ)，以及每一对( w¯0=(w0 1,…, w0 t) w¯1=(w1 1,…, w1 t))，满足(xi, w0 i) ∈ RL且(xi, w1 i) ∈ RL对于 i= 1,…, t成立，并且对于任意辅助输入 z， 以下集合是计算上不可区分的： {viewP(w¯0) V ∗(x¯,z)} and{viewP(w¯1) V ∗(x¯,z)}.

在[18],中展示了基于NIZK证明的两轮可重置的见证不可区分证明的构造， 随后在[27],中通过依赖特定数论假设展示了非交互式可重置的见证不可区分 证明，并从 iO[6]得出。

让我们回顾一下由 [3] 提出的可重置可靠性定义。

定义 9（可重置可靠论证 [3]）

作弊证明者 P∗对可重置验证者 V的重置 攻击由以下两步随机过程定义，该过程以安全参数 λ为索引。

1. 均匀选择并固定 t=poly(λ)条随机带，记为 r1，…， rt，用于 V，从而得 到确定性策略 V(j)(x)= Vx,rj，由 Vx,rj(α)=V(x, rj, α)定义，4其中 x ∈{0, 1}λ且 j ∈[t]。每个 V(j)(x)称为 V的一种化身。
2. 在输入 1λ时， 机器 P∗可启动与 V(j)(x)的 poly(λ)次交互。 P∗的活动以轮次进行。在每 一轮中， P∗选择 x ∈{0, 1}λ和 j ∈[t]，从而定义 V(j)(x)，并与之进行一次 完整会话。

设(P, V)是语言 L的一个交互式论证。我们称(P, V)是 L的可重置可靠论证， 如果满足以下条件：

–可重置可靠性：对于每次多项式大小的重置攻击，存在某个会话使得相应的 V(j)(x)已接受且 x∈/ L的概率是可忽略的。

定义10（承诺方案）

给定一个安全参数 1λ，一个承诺方案 com是两个 PPT交互式 算法（发送方 S和接收方 R）之间的一个两阶段协议。在承诺阶段 S，输入

这里， V(x, r, α) 表示策略 V 在公共输入 x 和随机带 r 上，在观察到消息序列 α 后 所发送的消息。

一条消息 m与 R交互以生成一个承诺 c=com(m)。在打开阶段， S向 R发送打开信息 d，使得 R接受 m作为 c的打开。

形式上，我们说com是一个完美绑定承诺方案，如果满足以下性质：

正承确诺性阶:段。设 c= com(m)为消息 m的承诺，该承诺是执行com时产生的 输出，其中 S以消息m作为输入运行。令 d为 S在此阶段的私有输出。

•打开阶段5。 R输入 m和 d接受 m作为 c的打开。

统计性（分别地，计算性）隐藏 [30]： 对于任意攻击者（分别地，PPT攻击者） A以及一个随机选择的比特 b ∈{0, 1}
统计性（分别地，计算性）隐藏 [30]： 对于任意攻击者（分别地，PPT攻击者） A以及一个随机选择的比特 b ∈{0, 1}，考虑以下隐藏实验 ExpHiding Ab,com（λ）：

• 输入 1λ后，攻击者 A输出一对长度相同的消息 m0、 m1。
• S在输入消息 mb后，与 A交互以生成mb的承诺。
• A输出一个比特 b′，这就是该实验的输出。

对于任何攻击者（或PPT攻击者） A，存在一个可忽略函数ν，使得：
∣ ∣ ∣ Pr[ExpHiding 0A,com(λ)= 1] − Pr[ExpHiding 1A,com(λ)= 1] ∣∣∣ < ν(λ).

统计（相应地，计算）绑定性：对于承诺阶段中由可能恶意且无界（相应地， 恶意PPT）的发送方生成的每个承诺comS∗，存在一个可忽略函数 ν，使得 S∗以至多 ν（λ）的概率输出两个公开值（m0, d0）和（m1, d1），其中 m0 = m1，且 R接受这两个公开值。

我们还说，一个承诺方案是完美绑定的当且仅当 ν(λ)= 0 .

本文中，我们考虑非交互式完美绑定计算隐藏承诺方案，该方案可基于一 对一单向函数 [22] 构造。两消息统计绑定承诺方案可基于单向函数 [28,32] 获 得。

定义11（伪随机函数（PRF））

一族函数{fs}s∈{0,1} ∗被称为伪随机的，如果对 于所有对抗性的PPT机器 A，对于每个正多项式 p()，以及足够大的 λ ∈ N，均成立
| Pr[Afs(1 λ )= 1] − Pr[A F (1 λ )= 1]| ≤
1 p(λ)
.
其中 |s| = n和 F表示一个真正随机函数。

本文中，我们仅考虑非交互式打开阶段。

定义12（不可区分性混淆）

对于确定性电路类{Cλ}λ∈N，如果一个均匀机器 iO满足以下条件，则称其为该电路类的 indistinguishabilityobfuscator： – Co正确性：对于所有安全参数 λ∈N，对于所有 C∈Cλ，对于所有输入 x，
Pr[Λ ← iO(1λ, C):Λ(x)= C(x)]= 1.
–安全性：对于每个非均匀PPT可采样的分布 D和攻击者 A，存在一个可忽 略函数 ν ，使得对于足够大的λ ∈ N，如果
Pr[(C1, C2, z) ← D: ∀x, C1(x)= C2(x)]> 1 − ν(λ),
then Pr[(C1, C2, z) ← D: A(iO(1λ, C1), z)= 1]
−Pr[(C1, C2, z) ← D: A(iO(1λ, C2), z)= 1] ≤ ν(λ).
我们说一个 iO是超多项式安全的，如果存在一个超多项式函数 T，使 得对于所有运行时间至多为 T(λ)的攻击者 A，上述条件均成立。

令 RU={((M, x, t) w)： M在 t步内接受(x, w)}， SU={(M, x, t)：∃w，((M, x, t) w) ∈ RU}且 RU(M, x, t) ={w：((M, x, t) w) ∈ RU}。令TM(x, w)表示 M在输 入(x, w)时所执行的步数。

定义13（通用论证 [2]）

一对交互式图灵机(P, V)称为一个通用论证系统， 如果它满足以下性质：

• 高效验证：存在一个多项式 p ，使得对于任意 y=(M, x, t)，（概率性） 验证者 V在公共输入 y上的总运行时间至多为 p(|y|)。特别地，协议中交换 的所有消息长度均小于 p(|y|)。
• 通过相对高效的证明者实现完备性：对于每 个((M, x, t) w) ∈ RU，
  Pr[〈P(w), V〉(M, x, t)= 1]= 1.
  此外，存在一个多项式 q，使得对于每个((M, x, t) w) ∈RU， P(w)在公共 输入(M, x, t)上的总运行时间至多为 q(|M| + TM(x, w)) ≤ q(|M| + t)。
• ˜–计算可靠性：对于每个多项式大小电路族{Pn}n∈N ，以及每一个(M, x, t) ∈{0, 1} n\ SU，存在一个可忽略函数 ν，使得
  Pr[〈 P˜n, V〉(M, x, t)= 1]< ν(n).
• –弱知识证明性质：对于每个正多项式 p ，存在一个正多项式 p ′和一个概率多 项式时间预言机机器 E ，使得以下条件成立：对于每个多项式大小的电路
  ˜族{Pn}n∈N，以及每个足够长的 y=(M, x, t) ∈{0, 1}∗，如果˜
  Pr[〈Pn, V〉(y)= 1]> 1/p(|y|)，那么
  Prr[∃w= w1… wt ∈ RU(y), ∀i ∈[t], EP˜n r(y, i)= wi]> 1/p′(|y|)
  ˜其中 EPn r表示通过将 E的随机带固定为 r˜并为其提供对 Pn的预言 机访问所定义的函数。

滥用符号表示，我们令 E为运行时间为 poly(n)·t 的预言机机器，用于提取整 个证据。我们称 E为全局知识证明提取器。注意， E不一定是多项式时间的。

定义14（不可区分见证的通用论证[2]）

一个通用论证系统(P, V)被称为不可 区分见证的（WIUA），如果对于每个多项式 p、每个多项式大小电路族 {V ∗ n}n∈N以及每三个序列 〈yn=(Mn, xn, tn)〉n∈N, 〈w1 n〉n∈N和 〈w2 n〉n∈N，满足 |yn| = n, tn ≤ p(|xn| )且(yn, w1 n)，(yn, w2 n) ∈ RU，则概率集合{〈P(w1 n) V ∗ n〉 (yn)}n∈N与{〈P(w2 n) V ∗ n〉(yn)}n∈N是计算上不可区分的。

定理 3[2] 。 假设存在抗碰撞性哈希函数族，则存在一个四轮公开硬币WIUA。

定义15（特殊稳健的不可区分见证证明 [11]）

对于语言 L ∈NP及其见证 关系RL的一个四轮公开硬币交互式证明，如果对于任意两个交互记录(δ, α, β, γ) 和(δ′, α′, β′, γ′)，其前两条消息(δ, α)和(δ′, α′)相同，但挑战 β和 β′不同， 则存在一个确定性过程可在多项式时间内从这两个交互记录中提取见证，则称 该证明关于 RL是特殊稳健的。对于 N P中的语言，具有见证不可区分性的特 殊稳健证明（WISSP）可基于单向函数构造。

定义16（ZAP [25]）

ZAP是由杜克和诺尔[18]提出的两轮公开硬币见证不可 区分性证明。ZAP还具有一个特殊性质：证明者发送的第一条消息可重复用于 多个证明。如[3],所述，任何ZAP系统已天然具备可重置可靠性。此外，通过 应用[8]中的变换，可以获得可重置的见证不可区分性。我们将所得系统称为 rZAP系统，其同时具备可重置可靠性和可重置的见证不可区分性。

2.1 P‐证书与可委托的CRS生成

对于 c ∈ N，令 Lc={(M, x, y)： M(x) 在 |x|c 步内完成。令 TM(x) 表示 M 在 输入 x 上执行的步数。

定义17（P-证书系统 [11]）

在CRS模型中，如果存在多项式 l CRS和 l π，使得对于 c、 λ ∈ N和 q=（M, x, y） ∈ L c，则PPT算法元组（Gen,Pcert, V cert）是一个 P‐证书 系统。

• CRS生成： CRS ← Gen(1λ, c)，其中Gen的运行时间为poly(λ)。 CRS的长 度被 lCRS(λ)所限制。
• 证明生成： π ←Pcert(1λ, c, CRS, q)，其中Pcert的运行时间为poly(λ,|x|, TM(x))，且满足 TM(x) ≤ |x|c。 π的长度被 lπ(λ)所限制。
• 验证证明： b= Vcert(1λ, c, CRS, q, π)，其中Vcert的运行时间为poly(λ, |q| )。

完备性 ：对于每个 c, d, λ ∈ N和 q=(M, x, y)∈ Lc，使得 |q| ≤ λd，
Pr[CRS ← Gen(1λ, c), π ← Pcert(1 λ, c, CRS, q): Vcert(1 λ, c, CRS, q, π)= 1]= 1.

强可靠性 ：存在一个超多项式函数 T(λ)= λω(1)和一个超常数函数 C(λ)= ω (1)，使得对于每个运行时间被 T(λ)限制的概率算法 P∗，都存在一个可忽略 函数 ν，使得对于所有 λ ∈ N和 c ≤ C(λ)，
Pr
⎡
⎣ (q, st) ← P∗(1λ, c), CRS ← Gen(1λ, c), π ← P∗(st, CRS) : Vcert(1 λ, c, CRS, q, π)= 1 ∧ q∈/ Lc
⎤
⎦ ≤ ν(λ).

一个 P-证书系统如果其CRS的生成两轮Gen还依赖于语句 q，即 CRS ← Gen(1λ, c, q)，则称为两轮 P-证书系统。该两轮 P-证书系统可被视为如下交互 协议：证明者向验证者发送 q；验证者回复 CRS ← Gen(1λ, c, q)；证明者发送 π ← Pcert(1 λ, c, CRS, q)；验证者在Vcert(1 λ, c, CRS, q, π)= 1时接受。

一个两轮 P-证书系统具有简单验证过程，如果验证算法Vcert仅依赖于安 全参数 1λ、CRS和证明 π，即它独立于语句 q和语言索引 c。在这种情况下， 我们将验证记为Vcert(1 λ, CRS, π)。

一个 P-证书系统是唯一的，如果对于每个 λ、 c ∈ N、 CRS、 q ∈{0, 1}∗，至多存 在一个 π ∈{0, 1}∗，使得Vcert(1 λ, c, CRS, q, π)= 1。

No请注意，a P‐证书的唯一性即使在面对无效公共参考串时也成立。

定义18（可委托的CRS生成 [11]）

一个两轮 P-证书(Gen,Pcert,Vcert)具有 可委托的CRS生成，如果 Gen由三个子程序组成：设置算法、PreGen和 CRSGen，并且存在多项式 ld和 lCRS满足以下性质：

• 参数生成：(P P, K) ←设置算法(1λ, c)，其中设置算法是概率性的，并在 poly(λ)时间内运行。 PP是公共参数， K是秘密参数。
• 语句处理： d= PreGen(P P, q)，其中 PreGen是确定性的，在 poly(λ, |q| ) 时间内运行，且 d 的长度由 ld(λ)界定，独立于 |q|。
• CRS生成： κ ← CRSGen(P P, K, d)，其 中 CRSGen是概率性的，在 poly(λ)时间内运行，且 κ的长度由 lCRS(λ)界 定。

Gen输出 CRS=(P P, κ)。

定理 4[11] 。 假设存在针对 P/poly的不可区分性混淆（iO）以及一个超多项 式安全的单射单向函数，则存在一个（超多项式安全的）两轮 P-证书系统，具 有（强）可靠性、唯一性和可委托的CRS生成。

3 常数轮可重置零知识

在[11],钟等人中，构造了一个常数轮并发零知识论证，其假设为存在抗碰撞哈 希函数族、单向置换以及针对 P/poly（具有略微超多项式安全性）的不可区 分性混淆器。我们在此将其表述如下： 令com为一个非交互式完美绑定、计算隐藏的承诺方案。如[11],所述， 该协议可以修改为使用基于单向函数的两消息统计绑定承诺方案[28,32]。令 {Hn}n∈N为一个抗碰撞性哈希函数族。令(Gen, Pcert, Vcert)是一个具有强可靠 性、唯一性和可委托CRS生成的两消息 P‐证书系统，其中Gen由子程序 (Setup, PreGen, CRSGen)组成。令 D= D(n)是一个超常数函数，使得在定 义17中， D(n) ≤ C(n) 对于 C(·)成立。令(PUA, VUA)为一个常数轮公币 WIUA。令(PSS, VSS)为一个常数轮公币WISSP。令(PZK, VZK)为一个常数轮 ZK论证。

设Πn,c3,PP,K,ρCRSGen和 Π′ n,c3,κ为如下定义的程序：

Πn,c3,PP,K,ρ CRSGen：输入(d, ρ)

1. 如果 c3 = com(d; ρ)，则输出 ⊥。
2. 输出 CRSGen(P P, K, d; ρCRSGen)。

Π′ n,c3,κ：输入为(d, ρ)

1. 如果 c3 = com(d; ρ)，则输 出 ⊥。
2. 输出 κ。

令 On V cert 为一个（确定性的） P‐证书预言机，其在输入 CRS时输出唯一的 π，使 得Vcert(1 n, CRS, π) = 1。

令Emun为一个确定性多项式时间机器，它在输入(S, y, σ)时，模拟确定性 预言机机器 S在输入y并访问预言机 On V cert 时的执行过程。Emun通过以下方式 模拟 On V cert ：在第i次来自 S的调用中，对输入 CRSi检查 πi是否满足Vcert(1 n, CRSi, π) = 1中的(π1, π2,…)。如果满足，则返回 πi给i，否则停止。

常数轮并发零知识论证 Γ[11]

证明者 P和验证者 V在公共输入 1n和 x，以及证明者的私有输入 w上：

1. V向 P发送h ← Hn。
2. P向 V发送com(0; ρ1)。
3. V向 P发送 r ←{0, 1}4n。
4. P向 V发送com(0; ρ2)。
5. P和 V运行(PUA, VUA)， 以证明以下语句：要么 x ∈ L，要么存在 S、 j ∈[m]、 s ∈{0, 1}n、 σ、 ρ1、 ρ2，使得– com(h(S); ρ1) 且 – com(h(q); ρ2)，其中 q=(Emun, (S, ( 1n, j, s) σ) r)。若 VUA拒绝，则V拒绝。
6. V运行 (P P, K) ← SetUp(1n, D) 并将 PP 发送给 P。
7. P向 V 发送 com(0; ρ3)。
8. P和 V运行 (PUA, VUA)，使得 P向 V证明：要么 x ∈ L成立，要么存在 q, ρ2, ρ3， 使得 c2= com(h(q); ρ2) 且 c3= com(d; ρ3)，其中 d= PreGen(PP, q)。若 VUA拒绝，则 V拒绝。
   ̂ ̂9. V计算 Π ← iO(Πn,c 3 ,PP,K,ρ CRSGen) 并将 Π 发送给 P。
9. V和 P运行 (PZK, VZK)，使得 V向 P证明存在 K,ρSetUp, ρCRSGen, ρiO，满足 – (P P, K) = SetUp(1n, D; ρSetUp) 且 ̂– Π= iO(Πn,c3,PP,K, ρCRSGen; ρiO)。若 VZK拒绝，则P中止。
10. P向 V发送 c4= com(0; ρ4)。
11. P和 V执行(PSS, VSS)，使得 P向 V证明：要么 x ∈ L成立，要么存在 d、 ρ3, ρ4， 使得 c3= com(d; ρ3)且 c4= com(CRS; ρ4)，其中̂ CRS=(PP,Π(d, ρ3))。如果 VSS拒 绝，则 V拒绝。
12. P和 V执行(PSS, VSS)，使得 P向 V证明：要么 x ∈ L成立，要么存在 CRS、 ρ4 以及 P‐证书 π，使得 c4= com(CRS; ρ4)且Vcert(CRS, π) = accept。如果 VSS接受， 则 V接受；否则， V拒绝。

定理 5[11] 。 假设存在抗碰撞性哈希函数族、单向置换以及对P/poly的超多项 式安全的不可区分性混淆器，则存在一个常数轮并发零知识论证协议用于 N P。

3.1 从并发零知识到可重置零知识

设 Γ=(PΓ , VΓ)是一个 轮的并发零知识论证。我们按如下方式构造一个 O()轮可 重置零知识论证 Λ：

令com为一个非交互式完美绑定且计算隐藏的承诺方案。令(PrsZK, VrsZK) 为一个具有模拟器SimrsZK的常数轮可重置可靠零知识论证。

常数轮可重置零知识论证 Λ

证明者 P和验证者 V在公共输入 1n和 x，以及证明者的私有输入 w上：

1. V向 P发送m0=(com(r1)…, com(r))。
2. P为伪随机函数 fs选择一个随机种子 s：{0, 1}∗ →{0, 1}l(n)，其中 l(n)是 PΓ在 Γ的每一轮中所 需随机比特数的上界。
3. P和 V执行 Γ，并进行如下修改：
   - 对于 VΓ 在 Γ的第 i轮中发送的每条消息 mi， V和 P运行(PrsZK, VrsZK)，使得 V 向 P证明 mi是使用在第一轮中承诺于 m0的随机比特 ri计算得到的。
   - 对于 PΓ 在 Γ的第 i轮中发送的每条消息 m′ i， P将fs应用于截至目前的 交互记录，并将输出用作随机比特来计算 m′ i。

3.2 证明

引理1 . Λ是一个可重置的零知识论证系统。

证明 。首先，我们考虑协议ΛF，其中我们将伪随机函数 fs替换为真正随机函数 F： {0, 1}∗ →{0, 1}l(n)。我们认为ΛF与Λ是不可区分的，理由是通过归约到伪随机函 数的安全性，具体如下。我们构造一个攻击者 APRF，其可访问一个 oracle，该 oracle 计算 fs 或 F，使得 APRF 运行 Λ（或 ΛF），并进行如下修改：对于 诚实的 P发送的每一条消息 m′ i， APRF使用当前协议交互记录作为输入向 oracle 查询，并将 oracle 的输出作为随机比特来计算 m′ i。最后， APRF运行并将 区分器在协议视图上的输出作为结果输出。由于 APRF从头到尾运行了诚实的 P， 因此它能够访问 P的私有参数，从而能够完成整个协议。因此，任何非均匀的多项 式大小的验证者的行为必须相同，除非以可忽略概率例外。

设 V ∗ RES 是 ΛF中的一个可重置验证者。我们构造一个并发验证者 V ∗ CONC ，使 得对于任意的 PCONC，存在 PRES，使得{viewP R E S V ∗ R E S }和{viewP CO N C V ∗ CO N C }计算上不可 区分，构造方式如下： V ∗ CONC 在内部运行V ∗ RES ，并在 V ∗ RES 和 P CONC之间传递消 息，同时记录 V ∗ RES 的第一条消息（承诺）以及 P CONC的每一条消息。

每当 V ∗ RES重置 PRES并发送第一条消息时， V ∗ CONC会检查该消息是否已发 送过。如果是，则 V ∗ CONC重新发送相应的响应，或在必要时继续该会话。否则， V ∗ CONC将启动一个 PCONC的新会话。该新会话中使用的随机性与将 F应用于 新交互记录（由于 m0不同）所使用的随机性不可区分。

声明 。 对于固定的种子 s 和m0，对于每个 i ∈[]， V ∗ r 无法以可忽略概率以外的 概率在第 i 轮找到两个不同的消息 mi, m′i，使得其能使 PRES 接受第 i 轮的可重置可 靠零知识论证。

证明 。设第一轮消息为m0=(c1,…, c)。假设存在矛盾，即存在 i ∈[]使得 V ∗ r 能够找到 mi = m′ i以及相应的可重置可靠零知识论证，且 PRES以不可忽略的 概率接受。在此情况下，根据该零知识论证的可重置可靠性， mi和 m′ i均是相 对于协议 ΛF正确计算得出的，其所用随机性已承诺于 ci中。换句话说，存在 一个确定性的多项式时间函数 μi，使得 mi和 m′ i具有形式 mi= μi(ri)，其中 ci=com(ri)，以及 m′ i= μi(r′ i)，其中 ci= com(r′ i)，对于某个 ri = r′ i成立。 然而，这意味着com(ri)= com(r′ i)，这与com的完美绑定性相矛盾。

因此，整个会话的交互记录仅依赖于 s和m0。因此，{viewPRES V ∗ RES} 和{ viewPCONC V ∗ CONC}是计算上不可区分的。

引理2 . Λ是可靠的。

证明 。假设存在一个作弊证明者 P∗ RES ，其能够以非可忽略概率证明一个错误 定理 x∈/ L。考虑以下混合实验：

Exp0：运行 〈P∗ RES, VRES〉(1n, x)。

令 Exp1,0 与 Exp0, 相同，且对于 i= 1,…, ，

Exp1,i：与Exp1,i−1类似，只是在消息mi之后对 PrsZK(ri)的执行被替换为 SimP ∗ RES, i rsZK的执行，其中 P ∗ RES,i是残余的rsZK验证者（注意 P ∗ RES运行 VrsZK）， 且已将 m0,…, mi作为输入接收。假设存在一个区分器 D能够区分Exp1,i和Exp1,i−1， 我们由此导出矛盾。接下来我们构造一个针对(PrsZK, VrsZK)的（标准）零知识性质 的区分器 D′。首先，我们均匀地生成 r1,…, ri−1, ri+1,…, r，并令 c˜i=为co m(0)。然后我们按照Λ的方式为 P ∗ RES生成交互记录，但使用 c˜i代替 ci= com(ri)。 根据com的计算隐藏性， P ∗ RES无法区分 c˜i和 ci。给定{viewP rsZK V rsZK }（其中 VrsZK 由P ∗ RES,i运行）或SimP ∗ R E S, i rsZK ，我们使用之前生成的 r j 来生成协议Λ的剩余部 分的交互记录。最后， D′在整个交互记录上运行 D 。无论哪种情况，该交互记 录在计算上均不可区分于Exp1,i或Exp1,i−1。因此， D′能够破坏(PrsZK, VrsZK)的 零知识性质，这导致矛盾。故Exp1,i与Exp1,i−1不可区分。

令 Exp2,0 与 Exp1, 相同，且对于 i= 1,…, ，

Exp2,i：类似于 Exp2,i−1 ，只是将第一条消息 m0 中的 com(ri) 替换为 com(0)。考虑以下归约到 com 的计算隐藏性质的过程： ri 和 0 被发送给 Scom； 它将来自 Scom 的承诺作为 Exp2,i−1（或 Exp2,i）中第 i 个承诺传入； Acom 可以 完成实验，因为它不需要知道使用 SimrsZK 承诺的是哪条消息； Acom 输出实验的 输出结果。计算隐藏性质意味着 Exp2,i 和 Exp2,i−1 是不可区分的。

现在我们通过在内部运行 Exp2,来为 Γ 构造一个作弊证明者 P∗ CONC： P∗ CONC 向 P∗ RES 发送 com(0)； P∗ c 将来自 P∗ RES 的每条消息传递给 VCONC； P∗ CONC 将来自 VCONC 的每条消息传递给 P∗ RES，然后运行 SimrsZK，同时 P∗ RES 运行 VrsZK。因此， P∗ CONC 可 以以非可忽略概率证明一个错误定理 x∈/ L，这与 Γ 的可靠性相矛盾。

定理6 . 假设存在单向函数，则存在一个编译器，可将 轮并发零知识论证转换 为 O()轮可重置零知识论证。

证明 。可重置零知识性和可靠性分别在引理1和2中证明。完备性由 Γ的完备性 直接得出。对于每一轮 Γ， P和 V必须额外运行 O(1)轮，用于 V采用承诺 的随机比特的可重置可靠零知识协议，以及在开始时多出1轮。因此，轮数复杂 度为 O()。

推论1 . 假设存在抗碰撞性哈希函数族、单向置换以及针对P/poly的超多项式安 全的不可区分混淆器，那么存在一个常数轮可重置零知识论证用于 N P。

证明 。我们通过让 Γ 成为 [11] 的常数轮并发零知识论证系统来实例化 Λ 。 完美绑定com可由单向置换构造。常数轮可重置可靠零知识论证可由单向函数 构造 [12]。

4 具有可重置可靠性的并发零知识

在本节中，我们基于[11]中的常数轮 cZK论证，构建一个具有可重置可靠性的 常数轮并发零知识论证。我们使用了上一节中的常数轮 rZK 论证（推论1）、 在[3]中用于向公币协议添加可重置可靠性的技术，以及我们提出的新技术来处 理[11]中 cZK 协议的非公币特性。

4.1 构造

令 Γ为第3节中描述的常数轮并发零知识论证。我们按如下方式构造具有可重 置可靠性的常数轮并发零知识论证 Δ：

设(PrZK, VrZK)为一个常数轮可重置零知识论证，其模拟器为SimrZK。验 证者 V选择一个伪随机函数 fs的随机种子 s：{0, 1}∗ →{0, 1}l(n)，其中 l(n) 是每轮交互中 V所需随机比特数的上界。然后 P和 V运行 Γ，并进行如下修改： 在步骤10中，不再运行零知识论证(PZK, VZK)，而是 V和P运行可重置零知识 论证(PrZK, VrZK)。此外，对于 V在 Γ中发送的每一条消息m， V使用 fs应 用于至此为止协议交互记录的输出作为随机比特来计算 m。

4.2 证明

在证明上述协议是一个具有可重置可靠性的并发零知识论证之前，我们考虑对协议 Γ在[11]中的另一种修改 Γ′{。首先， P和 V重复步骤7–9共 t次，其中 V对某 个 t= poly(n)使用相同的ρCRSGen。令步骤 7j–9j表示第 j次重复的步骤7–9。其次， 我们移除步骤10中的零知识证明，并将其替换为“P选择 i ∈[t]并将 i发送给 V”， 然后 P和 V继续执行协议的其余部分，忽略 j = i的步骤 7j–9j”。

引理3 . Γ′是一个可靠交互式论证。

证明 。我们严格遵循[11]中 Γ的可靠性证明，但需对步骤7–9的重复部分进行 必要的修改。假设存在一个非均匀的确定性多项式时间证明者 P∗和一个正多 项式p ，使得对于无穷多个 n ∈ N， P∗可以说服 V以非可忽略概率1/p(n)接 受 x∈/ L，从而导致矛盾。设 E为WIUA（PUA, VUA）的全局知识证明提取 器， E′为WISSP（PSS, VSS）的知识提取器。我们定义实验Exp，其运行 〈P∗, V〉（1n, x），并附加以下操作：

• 在步骤5中，令 P∗ prefix1 为已接收前缀1=(h, r)的剩余WIUA证明者（该前缀在 步骤1和3中接收）。运行 w1 ← E P ∗ 前缀 1 E失败，则停止并输出 ⊥。
• 在步骤7j中，对于 j= 1，. . . ， t，令P∗ prefix2,j为 已接收前缀2,̂的剩余WIUA证明者，该前缀由j、 h、 r、WIUA消息、 PP 和 9k在步骤1、3、5、6及 8k中针对 k= 1, . . . , j − 1组成。运行w2, j ← E P ∗ 前缀 2 j s2 ,j，其中 s2,j为均匀随机性。如果 E失败，则停止并输 出 ⊥。
• 在第12步中，令 P∗ prefix 3 为已接收前缀3 ̂的剩余WISSP证明者，该前缀 由 h, r、WIUA消息、 P P和 Π j在步骤1、3、5、6及 8j和 9j中针对 j= 1, . . . , t组成。运行 w3 ← E ′P ∗ 前缀 3 s 3 ，其中 s3为均匀随机性。如果 E′失 败，则停止并输出 ⊥。
• 在第13步中，令 P∗ prefix 4 为已接收前缀4的剩余 WISSP证明者，该前缀由第12步中的前缀3和WISSP消息组成。运行 w4 ← E ′P ∗ 前缀 4 s 4 ，其中 s4为均匀随机性。如果 E′失败，则停止并输 出 ⊥。
• 如果 V拒绝，则输出 ⊥。否则，
  • 解析 w1=(S, j, s, σ, ρ1, ρ2)。如果 w1 不具有此形式，则输出 ⊥。
  • 令 q=(Emun,(S,(1n, j, s) σ) r)。对于 j= 1,…, t，如果 w2,j =(q, ρ2,j, ρ3,j) 对于某 个 ρ2,j,ρ3,j 成立，则输出 ⊥。
  设 d= PreGen(PP, q)。如果 w3 =(d, ρ3,i, ρ4) 对于某个 ρ4成立，其中 i ∈[t] 是由 P∗ 在步骤10中选择的，则输出 ⊥。̂
  • 令 CRS=(PP,Π(d, ρ3,i)). 如果对于某个 π 有 w4 =(CRS, ρ4, π)，则输出 ⊥。
• 输出 (S, q, r)。

根据WIUA的弱知识证明性质和WISSP的特殊可靠性，当 P∗说服 V接受 x∈/ L时，提取器 E和 E′以非可忽略概率 1/p′(n)成功提取上述见证（而非定 理的实际见证）。由于com的完美绑定性质以及 H的抗碰撞性，最后一步中的 一致性检查将以除可忽略概率 ν(n)外的概率通过。在这种情况下，除可忽略概 率外，c3,j在第 7j步发送的是对所有 j= 1, . . . , t相同的 d= PreGen(P P, q)对 应的com(d; ρ3,j)。否则，我们可以构造一个作弊的WIUA证明者，以非可忽略 概率随机选择 j ∈[t]并承诺c′= c3,j，从而以 d′ = PreGen(P P, q)对 c′= com(d′; ρ′)进行承诺。这将破坏WIUA的可靠性̂。因此，除可忽略概率 ν′(n) 外， Πj的唯一输出是对所有j= 1, . . . , m均为CRSGen(P P, K, d, ρCRSGen) = κ。于是，̂Exp不输出 ⊥且每个Πj输出相同 κ的概率为 1/p′(n)−ν(n)−ν′ (n)，该概率是非可忽略的。我们将此事件称为好事件。

现在考虑一系列实验 Exp′ j ，其中 j ∈[t] 定义如下：Exp′ 0=Exp，且 Exp′ j 与 Exp′ j−1 的区别仅在于步骤 9j 中，我们将 Π̂j ←̂iO(Πn,c3,j,PP,K,ρCRSGen) 替换 为 Π′ j ← iO(Π′ n,c3,j,κ)，其中 κ= CRSGen(P P, K, d; ρCRSGen)。当好事件发生时， 根据 com 的完美绑定性质，Π′ n,c3,j,κ 和 Πn,c3,j,PP,K,ρCRSGen 以可忽略概率除外是功 能等价的。在这种情况下，Exp′ j−1 和 Exp′ t 可通过归约到 iO 而不可区分，具体如 下：DiO 执行 Exp′ j−1 （或 Exp′ j）直到步骤 8j