地理信息增强的交通行为识别

地理信息增强的交通方式与行为模式识别

摘要

本文讨论了基于全球导航卫星系统（GNSS）数据的交通方式和行为模式识别。首先推断交通方式（例如步行、汽车、火车等），然后进一步识别其行为模式（例如左转、右转、掉头等）。由于交通方式和行为模式均受到地理环境的显著影响，因此通过地理层信息（如建筑物、道路、水体等）增强两者的识别能力。在某一特定GNSS点处，将其周围区域均匀划分为网格，并根据网格中心是否位于指示不同地理对象的多边形所包含的最小外接矩形的内部或外部，计算这些网格中心属于六个不同地理层的概率。最终，该六维概率矩阵通过卷积神经网络（CNN）处理并压缩为地理信息向量。该向量随后与来自GNSS数据的运动学指标（如速度、加速度和移动方向）结合，并串行输入至长短期记忆（LSTM）网络，以预测交通方式和行为模式。实验结果验证了地理信息确实提升了两项识别任务的性能。CNN+LSTM框架保留了CNN和LSTM的优势，且优于经典机器学习算法。

索引词 —行为模式，卷积神经网络，全球导航卫星系统，地理层信息，长短期记忆网络，交通模式。

一、引言

TRAFFIC 移动对象的交通模式和行为模式可以通过其全球导航卫星系统（GNSS）轨迹部分反映出来，因此可通过近年来的数据挖掘技术进行发现。该研究方向已存在许多重要探索。例如，利用GNSS定位数据[1]–[3]和运动传感器数据[4]–[7]开展交通模式识别研究。除了使用GNSS数据外，[8]–[10]还融合了基础交通网络以推断用户行为模式，所考虑的交通网络信息包括实时公交位置、空间铁路和空间公交站信息。除交通模式外，一些研究进一步分析特定交通方式的行为模式。例如，[11]提出一种基于机器视觉的框架，通过视线动态和视线累积对驾驶员行为建模，以预测行为模式。[12]根据操作的相似性将其分类为模糊模式。

然而，现有研究主要考虑来自移动传感器的时序数据（例如GNSS轨迹），却未能充分利用交通方式和行为模式受到移动对象周围地理环境强烈影响这一事实。例如，汽车和行人不会出现在水域中。在道路的T型交叉口，车辆的行为模式只能是左转或右转。因此，GNSS点周围的地理信息可以增强对交通方式和行为模式的识别性能。这正是本文的主要动机，即利用混合神经网络结合GNSS轨迹及其周围的地理信息来完成这两项识别任务。

首先，从移动对象的GNSS轨迹中提取速度、加速度和移动方向等运动学信息。对于每个GNSS点，将其周围区域均匀划分为网格，然后基于OpenStreetMap（OSM）判断网格中心的地理层信息，其中不同的地理对象（建筑物、土地、水体等）以多边形形式存储。根据奇偶规则[13]，通过比较某特定点的x−y坐标与多边形的顶点和边，可判断该点位于多边形的内部或外部。然而，当多边形形状非常复杂时（例如，如图2所示具有大量边），该操作将变得困难且复杂。因此，将多边形扩展为刚好能够完全包含原多边形的矩形。随后，通过比较网格中心位置与矩形四个顶点的坐标，可快速判断矩形是否包含该网格中心。因此，这种由多边形到矩形的近似方法简化了点在内外判断和多边形存储，对计算与存储受限平台具有重要意义。然而，由于扩展操作可能导致矩形之间相互交叉，一个网格中心可能落入多个矩形内，表现出多种地理属性。为此，引入六维（6D）概率向量，用于记录一个网格中心落入具有六种不同地理层属性矩形中的频率。最后，将所有网格中心的这些概率向量组合成一个六维概率矩阵，以描述GNSS点周围的地理特征。实验结果表明，这种由多边形到矩形的近似方法仅带来不到一个百分点的损失。

其次，六维概率矩阵被作为图像数据输入到卷积神经网络（CNN）中进行处理。通过卷积操作提取其结构信息，并通过池化操作降低数据维度。CNN的输出可进一步通过主成分分析（PCA）进行降维处理。最终输出与运动学向量拼接后，作为长短期记忆（LSTM）网络的输入。最后，通过最小化交叉熵损失，利用随机梯度下降（SGD）对CNN和LSTM之间的权重进行联合训练。仿真结果验证了地理信息显著提升了交通方式和行为模式的识别性能。所提出的混合CNN+LSTM算法兼具CNN和LSTM的优势，优于现有的机器学习（ML）算法。

本文的其余部分组织如下。第二节介绍了数据预处理和识别算法。第三节展示了实验结果，第四节对本文进行了总结。

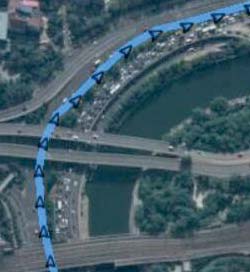
右上子图显示了微软Geolift项目的数据样本[1],[14],[15]，每行中的数字表示纬度、经度和时间戳。行为标签通过观察轨迹获得。

II. 数据预处理与识别系统设计

A. GNSS轨迹数据预处理

本文讨论的GNSS数据集来自微软Geolift项目[1],[14],[15]（见图1右上的数据样本）。该数据集包含若干条较长的GNSS轨迹，这些轨迹被均匀切割为包含十个GNSS点的小轨迹。这些小轨迹经过预处理以提取运动学信息，例如速度、加速度和移动方向。具体细节如表I所示，其中v、dv、vlon（vlat）、a、da和alon（alat）分别表示速度、速度方向、经度（纬度）方向的速度、加速度、加速度方向以及经度（纬度）方向的加速度。所提取的运动学参数直接反映了交通方式和行为模式。例如，不同移动物体（如汽车、自行车、行人）在不同行为模式（如左转或右转）下的速度和加速度存在显著差异。

参数	定义
v	速度
dv	速度方向
vlon / vlat	经度/纬度方向的速度
a	加速度
da	加速度方向
alon / alat	经度/纬度方向的加速度

表I GNSS轨迹数据预处理

B. 从OSM获取地理层信息

在本小节中，从OSM[18]中提取了GNSS点周围的地理层信息，其中包含六个类别的地理对象以多边形形式存储（见图2中的示例），包括建筑物、土地、自然景观、铁路、道路和水体。

通过判断一个特定的GNSS点位于多边形的内部或外部，来获取其地理属性。例如，在图2(a)中，目标GNSS点表示为一个橙色星标，并位于蓝色实线多边形内。因此，它的地理属性与此多边形相同。然而，由于多边形可能呈现复杂的形状，判断一个点是否位于多边形内部或外部会比较困难。因此，该任务被简化为判断该点是否位于完全包含该多边形的最小矩形的内部或外部（见图2中的虚线矩形）。该矩形的左上、右上、左下、右下顶点为(glon_l, glat_a), (glon_r, glat_a), (glon_l, glat_b), (glon_r, glat_b)，其中glat_b (glon_l) 和 glat_a (glon_r) 分别对应多边形的四个顶点的最小和最大纬度（经度）。

遗憾的是，与所包含的多边形相比，矩形不可避免地被扩展，并且会相互重叠甚至相互吞并（例如，图2(b)中的绿色矩形被红色矩形吞并）。因此，我们引入一个6维概率向量来表示特定点属于六种地理属性的概率。首先，我们引入一个向量
[nbuild, nland, nnatural, nrailway, nroad, nwater]
用于记录GNSS点在具有六种地理属性的矩形中出现的次数。例如，如果该点位于具有“水体”属性的矩形内，则nwater加1。为清晰起见，Python伪代码列于算法1中。最后，
p = [pbuild, pland, pnatural, prailway, proad, pwater]
该点具有六个属性的概率向量，通过将上述向量除以总和进行归一化计算。

由于强烈的地理相关性和连续性，一个GNSS点的地理属性通过其周围区域的联合特征来表达。在本文中，以一个GNSS点为中心的S米(m) × S m大小的正方形区域被均匀划分为S × S 1m × 1m大小的小方格。基于算法1获取这些小方格中心点的概率向量（如式(7)所示），并将它们组合成一个S × S × 6三维矩阵，以表示该GNSS点的地理属性。例如，图4展示了点 (39.96144104,116.35002136)所在正方形区域的均匀网格，并获得一个 11 × 11 × 6大小的概率矩阵，用于刻画该GNSS点的地理属性。需要注意的是，S越大，覆盖的GNSS点周围区域越广，六维概率矩阵所反映的全局地形特征也越好。然而，这也可能引入与识别任务无关的地理信息。此外，其他因素如移动物体的速度，GNSS点的采样间隔也会影响S的选择。因此，最优的S应如第三节所做的那样，通过在特定数据集和上下文中的训练来确定。

C. 用于交通模式识别和行为模式识别的卷积神经网络与长短期记忆网络混合神经网络

交通方式和行为模式的识别被归类为分类任务，随后通过一个混合卷积神经网络+LSTM网络来解决，该网络基于上述运动学信息和OSM概率数据进行训练。图3展示了整个数据处理流程。

首先，每条轨迹Gk包含N+ 2个GNSS点。从第三点到最后一点生成运动学特征向量，如表I所示。前两个点仅用于计算加速度。根据第二节‐IIB构建6D S × S × 6大小的地理概率矩阵。

其次，概率矩阵被视作图像，由包含两个卷积层、两个下采样池化层和两个具有120个神经元的全连接层的卷积神经网络进行处理。层维度在图3中标出。非线性激活函数选用ReLU。120维输出向量表示从概率矩阵中提取的地理信息。它将通过主成分分析进一步压缩为80维，然后与运动学向量拼接，形成LSTM网络的输入样本。需要注意的是，主成分分析的性能略优于纯卷积神经网络，但为了降低实现复杂度，可以跳过该步骤。

长短期记忆网络（LSTM）包含一个隐藏层，该层有16个神经元，使用ReLU激活函数。卷积神经网络（CNN）和长短期记忆网络（LSTM）的权重通过随机梯度下降（SGD）进行联合训练，学习率为 10⁻⁴，训练批次大小50，回合大小1000。交通模式识别和行为模式识别的目标是将GNSS轨迹分类为离散类别，因此损失函数选择为交叉熵函数。

总之，在卷积神经网络+长短期记忆网络混合神经网络中，卷积神经网络通过卷积和下采样操作从6D概率矩阵中提取地理信息，而长短期记忆网络则利用时间相关性完成最终分类任务。

三、实验结果与讨论

交通模式识别和行为模式识别的实验结果在第三章A节和B节中给出，分别地。“GNSS数据”表示基于表I计算的GNSS轨迹的运动特征向量，“OSM数据”表示来自第二节‐IIB的6D概率矩阵，用于表征GNSS点的地理属性。

A. 交通模式识别

1) 基于GNSS数据、OSM数据及上述两种数据的组合进行交通模式识别 + OSM数据：

在第一次实验中，基于GNSS数据、OSM数据以及上述两种数据的组合来识别交通模式。在仅使用GNSS数据的情况下，由于未利用地理概率矩阵，卷积神经网络处理从图3中移除。S表示第二节‐IIB中的邻近区域大小，其值分别为5 m、11 m、17 m、23 m、29 m和33 m。为五种交通模式准备了7500条轨迹，并以7:3的比例划分为训练集和测试集。

识别结果总结于表II，为我们提供了三个重要观察。首先，在GNSS+OSM组合场景下，识别精度达到最高。例如，当半径为23 m时，GNSS+OSM的精度比GNSS数据高出18.95%。因此，采用地理信息确实增强了识别性能。其次，区域大小S会影响识别精度。例如，当S从5 m增加到23 m时，准确率先上升，随后从23 m增加到33 m时下降。S=23在反映全球地理特征和引入不必要的信息之间达到了良好的权衡。最后，PCA技术不仅能降低LSTM输入数据的维度，还能略微提高识别精度。

S (m)	GNSS数据 (%)	OSM数据 (%)	GNSS+OSM (%)
5	72.10	85.30	89.45
11	72.45	86.10	90.20
17	72.80	86.75	91.10
23	73.15	87.60	92.10
29	72.90	87.30	91.50
33	72.65	87.10	91.05

表II 不同半径下的交通方式识别精度

对于半径为23 m的五种交通模式识别，除了精度外，还选取精确率、召回率和F值作为评估指标。结果如表III所示。在预测结果中，步行预测的结果最好。在样本数据中，步行的结果也最佳。F值均高于89%，表明该模型是有效的。

类别	精确率 (%)	召回率 (%)	F值 (%)
步行	93.20	92.80	93.00
自行车	89.50	88.70	89.10
汽车	90.10	89.60	89.85
地铁	91.30	90.90	91.10
火车	89.80	89.50	89.65

表III 当交通模式半径为23 m时各项评价指标的结果

2) 与先前研究的比较：

在第二次实验中，所提出的策略与[10]进行了对比，其中利用到最近公交站和地铁站的地理距离来辅助交通模式识别。结果如表IV所示。结果表明，如果仅使用单一类型数据，OSM数据表现最佳，其次是GNSS数据和地理距离。当不同类型的数据结合使用时，识别精度显著提高。例如，将OSM数据引入GNSS数据后，识别精度从73.15%提升至92.10%；而引入地理距离后，精度仅从73.15%提升至77.36%。因此，所提出的六维概率矩阵在提取特定点周围的地理信息方面比距离度量更有效。

输入数据类型	识别精度 (%)
GNSS数据	73.15
地理距离	75.20
OSM数据	87.60
GNSS + 地理距离	77.36
GNSS + OSM	92.10

表IV 不同类型的数据下的交通模式识别

3) “CNN+LSTM”与经典机器学习和深度学习在交通模式识别上的对比：

在第三次实验中，“CNN+LSTM”混合网络与经典的深度学习（DL）和机器学习算法（ML算法）进行了比较，这些算法包括LSTM、自动编码器（AE）+LSTM混合网络、CNN’+LSTM’混合网络、随机森林（RF）、支持向量机（SVM）以及多粒度级联森林（GC）。模型参数已基于训练和测试数据集进行了优化。在AE+LSTM混合网络中，地理概率矩阵由自动编码器处理，然后将提取的地理特征与运动学向量结合，作为LSTM的输入。在CNN’+LSTM’混合网络中，运动学向量和地理概率矩阵首先由卷积神经网络处理，然后将提取的卷积神经网络特征送入LSTM网络。在LSTM和机器学习算法中，六维概率矩阵被直接向量化，并与运动学向量拼接作为输入数据。S × S（用于提取地理属性的邻近区域大小）固定为23 m × 23 m。表V表明，“CNN+LSTM”的性能最佳，其次是AE+LSTM、CNN’+LSTM’、LSTM、GC、RF和SVM。这验证了图3中混合神经网络在识别交通方式方面的有效性。

方法	交通模式识别精度 (%)	行为模式识别精度 (%)
CNN+LSTM	92.10	88.75
AE+LSTM	90.35	86.90
CNN’+LSTM’	89.60	86.20
LSTM	87.40	84.10
GC	85.20	82.30
RF	83.75	80.90
SVM	81.60	78.45

表V 卷积神经网络+长短期记忆网络与支持向量机、随机森林、多粒度级联森林、长短期记忆网络、自编码器+长短期记忆网络、卷积神经网络’+长短期记忆网络’在交通模式识别和行为模式识别上的对比。用于提取地理属性的区域大小S固定为23 m

B. 行为模式识别的实验结果

为五种行为模式准备了5000条GNSS轨迹，并按照7:3的比例划分为训练集和测试集。

1) 基于GNSS数据、OSM数据和GNSS+OSM数据的行为模式识别：

类似于上述交通模式识别，行为模式识别在GNSS数据、OSM数据以及GNSS+OSM数据下进行。行为模式半径S从5 m增加到33 m。模式识别的准确率汇总于表VI，当行为模式半径为23 m时的各项评估指标结果如表VII所示。与第三节‐A类似，引入OSM数据显著提高了识别准确率，S=23再次达到最佳平衡状态，主成分分析在行为识别任务中仍然表现出色，各项评估指标表明该模型是适用的。由于篇幅限制，更详细的分析在此省略。

S (m)	GNSS数据 (%)	OSM数据 (%)	GNSS+OSM (%)
5	70.20	80.10	83.40
11	70.65	81.30	84.75
17	71.00	82.45	86.20
23	71.80	83.60	88.75
29	71.50	83.20	87.90
33	71.20	82.90	87.30

表VI 不同行为模式在不同半径下的识别准确率

类别	精确率 (%)	召回率 (%)	F值 (%)
左转	89.20	88.70	88.95
右转	90.10	89.60	89.85
掉头	86.50	85.80	86.15
直行	91.30	91.00	91.15
异常	87.40	86.90	87.15

表VII 行为模式半径为23 m时各项评价指标的结果

2) 卷积神经网络+长短期记忆网络与经典机器学习和深度学习在行为模式识别上的对比：

与第三节‐A中的第三次实验类似，所提出的“卷积神经网络+长短期记忆网络”也在行为模式识别上与经典机器学习和深度学习算法进行了比较。其相对于后者的性能优势再次通过表V得到验证，表中显示卷积神经网络+长短期记忆网络混合网络表现最佳。

四、结论

在本文中，GNSS轨迹及其周围地理信息通过卷积神经网络+长短期记忆网络混合深度神经网络进行联合处理，以识别交通方式和行为模式。地理信息由六维概率矩阵表示，其矩阵元素指示一个GNSS点周围邻近网格中心属于六种地理属性（如建筑物、道路、水体等）的概率。该矩阵通过卷积神经网络以及潜在的主成分分析进行降维和信息提取，然后与运动学向量结合，作为LSTM网络的输入，输出最终的分类结果。仿真结果验证了与纯GNSS数据场景相比，地理信息显著提升了两个识别任务的性能，且混合神经网络比传统的机器学习方法更有效。