jzoj 5970.【北大2019冬令营模拟12.1】space 莫比乌斯反演

Description



Input

Output

Sample Input
2
1 2
2 1
1 2
2 1

Sample Output
24

样例解释：

Data Constraint

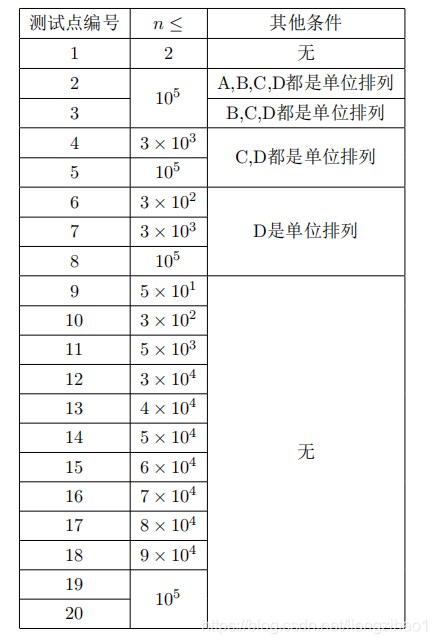
分析：
对于每一维都是若干环。因为每一个维互相独立，我们每一维选了一个环，大小为$i$，$j$，$k$，$l$，走回原点的步数是$lcm(i,j,k,l)$。而总共的点数是$i\ast j\ast k\ast l$，所以跳环要用$\frac{i\ast j\ast k\ast l}{lcm(i,j,k,l)}$。
我们只需找出跳环的步数，最后加上$n^4$即可。
设$A[i]$为第一维，大小为$i$的环的数目，$B[i],C[i],D[i]$同理，而跳环步数可以表示成，
$$\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1}^n\sum _{l=1}^n\frac{i\ast j\ast k\ast l}{lcm(i,j,k,l)}\ast A[i]\ast B[j]\ast C[k]\ast D[l]$$
因为不同的个数只有$\sqrt{n}$个，这样做是$O(n^2)$的。
而因为，
$$\frac{i\ast j\ast k\ast l}{lcm(i,j,k,l)}=\frac{lcm(i,j)\ast lcm(k,l)}{lcm(i,j,k,l)}\ast \frac{i\ast j}{lcm(i,j)}\ast \frac{k\ast l}{lcm(k,l)}$$
也就是
$$gcd(i,j)\ast gcd(k,l)\ast gcd(lcm(i,j),lcm(k,l))$$
设$x=lcm(i,j)$，$y=lcm(k,l)$，
可以看做有$gcd(i,j)$个$x$和$gcd(k,l)$个$y$然后求$gcd$和。
我们可以设一个$lim$，大于$lim$的部分直接暴力，小于$lim$的用反演。
$lim\approx 10^6$

代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#define LL long long

const int maxn=1e5+7;
const int maxp=1e6;
const LL mod=998244353;

using namespace std;

int n,cnt;
int a[maxn],vis[maxn];
int prime[maxp+7],not_prime[maxp+7],phi[maxp+7];
LL ans;
LL F[maxp+7],G[maxp+7],sum[maxp+7];

struct rec{
	LL x,y;
};

struct node{
	vector <rec> A,B;
}cir[4];


void getphi(int n)
{
	phi[1]=1;
	for (int i=2;i<=n;i++)
	{
		if (!not_prime[i])
		{
			prime[++cnt]=i;
			phi[i]=i-1;
		}
		for (int j=1;j<=cnt;j++)
		{
			if (i*prime[j]>n) break;
			not_prime[i*prime[j]]=1;
			if (i%prime[j]==0)
			{
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
			else phi[i*prime[j]]=phi[i]*(prime[j]-1);
		}
	}
}

LL gcd(LL x,LL y)
{
	LL r=x%y;
	while (r)
	{
		x=y;
		y=r;
		r=x%y;
	}
	return y;
}

LL lcm(LL x,LL y)
{
	return x*y/gcd(x,y);
}

void merge(node &a,node b)
{
	memset(sum,0,sizeof(sum));	
	for (int i=0;i<a.A.size();i++)
	{
		for (int j=0;j<b.A.size();j++)
		{
			LL x=gcd(a.A[i].x,b.A[j].x),y=lcm(a.A[i].x,b.A[j].x);
			LL z=a.A[i].y*b.A[j].y%mod*x%mod;
			if (y<=maxp) sum[y]=(sum[y]+z)%mod;
			        else a.B.push_back((rec){y,z});
		}
	}
	a.A.clear();
	for (int i=1;i<=maxp;i++)
	{
		if (sum[i]) a.A.push_back((rec){i,sum[i]});
	}
}

void getans(node a,node b)
{
	for (int i=0;i<a.A.size();i++) F[a.A[i].x]=(F[a.A[i].x]+a.A[i].y)%mod;
	for (int i=0;i<b.A.size();i++) G[b.A[i].x]=(G[b.A[i].x]+b.A[i].y)%mod;
	for (int i=1;i<=maxp/2;i++)
	{
		for (int j=i+i;j<=maxp;j+=i)
		{
			F[i]=(F[i]+F[j])%mod;
			G[i]=(G[i]+G[j])%mod;
		}
	}			
	for (int i=1;i<=maxp;i++) ans=(ans+F[i]*G[i]%mod*(LL)phi[i]%mod)%mod;	
	for (int i=0;i<a.A.size();i++)
	{
		for (int j=0;j<b.B.size();j++)
		{
			LL k=gcd(a.A[i].x,b.B[j].x);
			ans=(ans+a.A[i].y*b.B[j].y%mod*k%mod)%mod;
		}
	}
	for (int i=0;i<a.B.size();i++)
	{
		for (int j=0;j<b.A.size();j++)
		{
			LL k=gcd(a.B[i].x,b.A[j].x);
			ans=(ans+a.B[i].y*b.A[j].y%mod*k%mod)%mod;
		}
	}
	for (int i=0;i<a.B.size();i++)
	{
		for (int j=0;j<b.B.size();j++)
		{
			LL k=gcd(a.B[i].x,b.B[j].x);
			ans=(ans+a.B[i].y*b.B[j].y%mod*k%mod)%mod;
		}
	}
}

int main()
{
	freopen("space.in","r",stdin);
	freopen("space.out","w",stdout);
	scanf("%d",&n);
	for (int T=0;T<4;T++)
	{
		memset(sum,0,sizeof(sum));
		for (int i=1;i<=n;i++)
		{
			scanf("%d",&a[i]);
			vis[i]=0;
		}
		for (int i=1;i<=n;i++)
		{
			if (!vis[i])
			{
				int j=i,num=0;
				while (!vis[j])
				{
					vis[j]=1;
					num++;
					j=a[j];
				}
				sum[num]++;
			}
		}		
		for (int i=1;i<=n;i++)
		{
			if (sum[i]) cir[T].A.push_back((rec){i,sum[i]});
		}
	}	
	getphi(maxp);
	merge(cir[0],cir[1]);
	merge(cir[2],cir[3]);
	getans(cir[0],cir[2]);
	ans=(ans+(LL)n*(LL)n%mod*(LL)n%mod*(LL)n%mod)%mod;
	printf("%lld\n",ans);
}