leetcode 1569. Number of Ways to Reorder Array to Get Same BST（重新排序数组以获得相同 BST 的方法数）

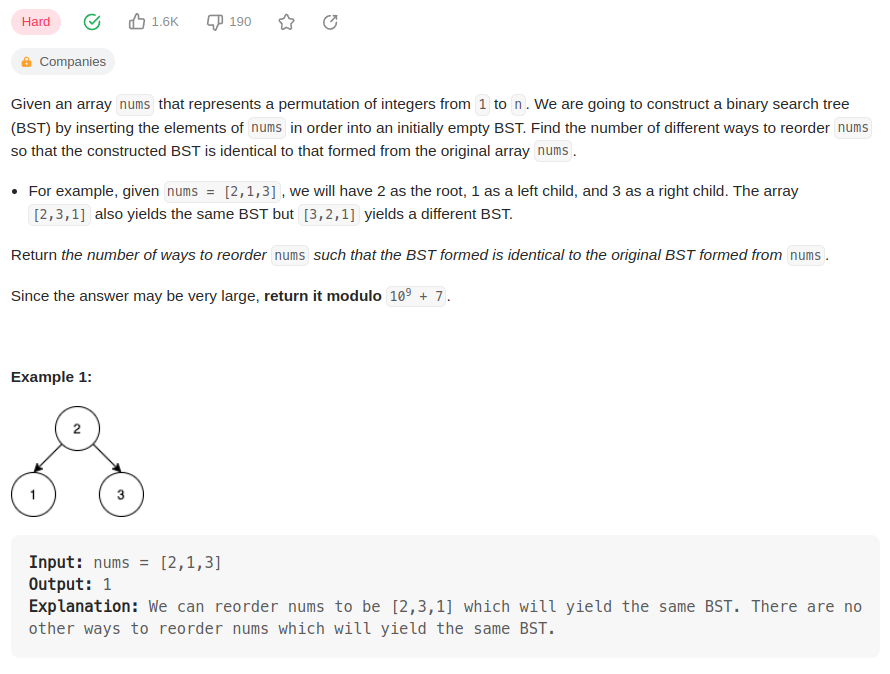
数组nums中包含1～n 数字的组合。
把nums中的数字按顺序建立一个初始BST，
重新排列nums中的数字，建成的BST和初始BST相同，问有多少种排列方法。

思路：

建立BST时，index为0处的元素为root, 后面 < root 的作为左子树，> root 的作为右子树。
想要和初始BST一样，root肯定是固定不动的。

需要重新排列的是root右边的左子树和右子树。

举个例子，[4,6,5,1,2,3],
4是root, [1,2,3] 是左子树，[6,5]是右子树。
先不考虑[1,2,3],[6,5]的排列组合，先就保持这个顺序，那么这5个数字不管怎么交叉放置都是[1,2,3]是左子数，[6,5]是右子数。
比如变成[4,1,6,5,2,3], root是4不变，<4的还是[1,2,3]， > 4的还是[6,5]

所以，上面的例子中，root 4右边有5个位置，选3个位置放1,2,3, 就有$C_5^3$种，剩下的位置放右子树的2个数字。
左子树和右子树内部又可以排列组合，
最终的排列数就是$C_5^3$ * combination(left) * combination(right)

左子树，右子树内部的排列组合就是递归这一过程。

下面就是如何计算组合数combination，Python可以直接用comb函数。
非python的看下面。
组合公式是$C_n^k=n!/k!$, 直接用阶乘 一是计算量太大；二是有除法，不能保证精确性。

不过可以观察到，组合数其实是个杨辉三角。
第一行是$C_0^0$, 第2行是$C_1^0$, $C_1^1$,
第3行是$C_2^0$, $C_2^1$, $C_2^2$, …

       1
      1 1
     1 2 1
    1 3 3 1

假设杨辉三角保存在table数组中，那么$C_n^k$=table[n][k]

总结一下，数组长度为n, root是nums[0], root右边有n-1个位置，
取其中left个位置放左子树的数字，剩下的位置放右子树的数字，
左子树和右子树再递归这一过程。
排列数会包含nums本身，所以最后要-1.

总的排列数就是($C_{n-1}^{left}$ * combination(left) * combination(right) - 1) % mod

这里建杨辉三角时，static会比instance函数更快

class Solution {
    private static final long MOD = 1000000007;
    //提前计算好组合数
    private static final long[][] COMB = pascalsTriangle(1000);

    public int numOfWays(int[] nums) {
        //nums转List
        List<Integer> arr = Arrays.stream(nums).boxed().collect(Collectors.toList()) ;
        
        return (int)((combination(arr)-1) % MOD);
    }

    long combination(List<Integer> nodes) {
        int n = nodes.size();
        if(n <= 2) return 1;

        List<Integer> left = new ArrayList<>();
        List<Integer> right = new ArrayList<>();

        int root = nodes.get(0);
        for(int i = 1; i < n; i++) {
            int cur = nodes.get(i);
            if(cur < root) left.add(cur);
            else right.add(cur);
        }
       
        long leftComb = combination(left) % MOD;
        long rightComb = combination(right) % MOD;
        return COMB[n-1][left.size()] * (leftComb * rightComb % MOD) % MOD;
    }

    //用static会更快
    static long[][] pascalsTriangle(int n) {
        long[][] comb = new long[n][n];
        for(int i = 0; i < n; i++) comb[i][0] = comb[i][i] = 1;

        for(int i = 2; i < n; i++) {
            for(int j = 1; j < i; j++) {
                comb[i][j] = (comb[i-1][j-1] + comb[i-1][j]) % MOD;
            }
        }
        return comb;
    }
}