卡尔曼滤波详解（paper加源码）

卡尔曼滤波广泛应用于智能导航与跟踪算法中，本文根据参考paper详解卡尔曼滤波原理，并结合matlab源码更好地理解paper

前期概念：
信号可以如下表示：

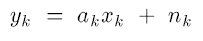
$y_k$是观测信号，$a_k$是增益，$x_k$是信息，$n_k$是noise
目标是估计$x_k$，
估计值${\hat{x}}_k$和真实值$x_k$之间的误差为

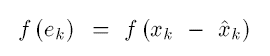
如果用平方误差，则

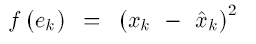
估计一段时间的误差则是求期望值

用最大似然推导，即是最大化估计x时y的概率：

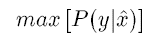
假设加性噪声是高斯分布，则：

$K_k$是归一化常数，则最大似然函数(期望值)为

取log

卡尔曼滤波推导：
state空间
在过程中的状态：

$x_k$是k时刻的状态向量，$\Phi$是k时刻状态到k+1时刻状态的状态转移矩阵，是不随时间变化的，$w_k$是方差已知的噪声。
观测值

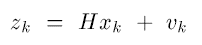
$z_k$是k时刻$x_k$的实际观测值，H是状态向量到measurement向量的连接矩阵，不随时间变化，$v_k$是measurement error，不随时间变化，也是方差已知的白噪声。

前面最大似然处的推导可知，用MSE估计最优filter的前提是error必须是高斯分布。两个噪声的协方差用以下变量表示

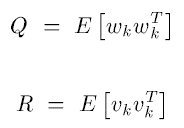
假设${\hat{x}}_k^{\prime }$是${\hat{x}}_k$的前一个估计，$K_k$是卡尔曼增益，那么

所以

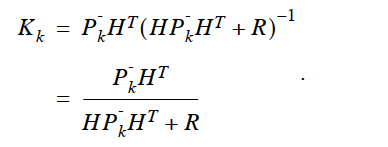
k时刻的误差协方差矩阵为

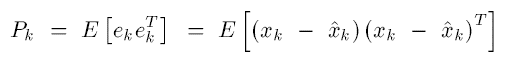
状态映射为下式

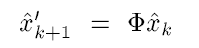
所以误差

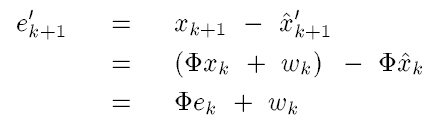
因此

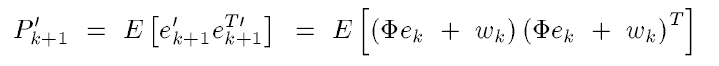
上式中$e_k$和$w_k$是不相关的，因为噪声$w_k$只是在k时刻和k+1时刻之间的噪声，而误差$e_k$则是从开始积累到k时刻的误差，因此

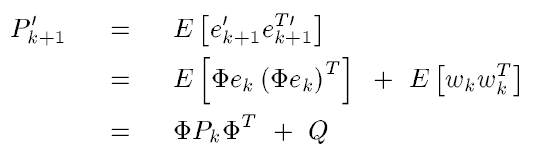
代码中上面的$\Phi$用矩阵A表示

最终卡尔曼滤波的两步，predict和correct分别做如下的工作

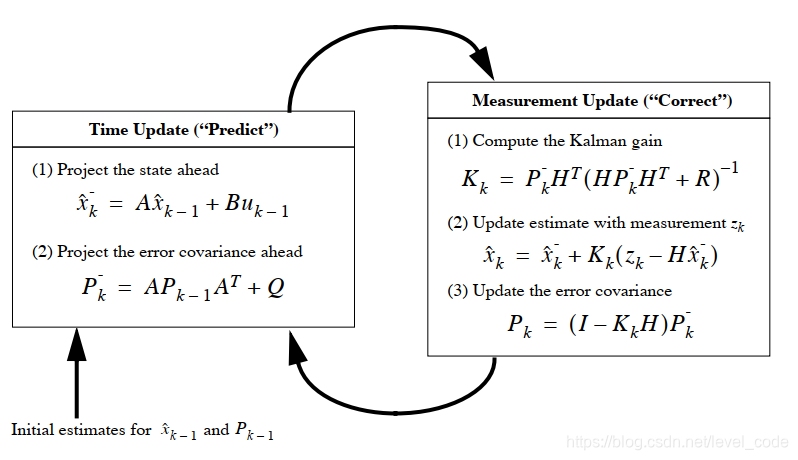
具体怎么用，结合matlab代码中的predict和correct来说明
matlab代码可参照示例
示例为小球的跟踪

跟踪首先要有目标的初始位置，这个位置可以是人为规定，也可以是检测算法检测出来。该示例中采用检测算法得到初始位置，correct函数中也是用每帧检测到的位置来更新卡尔曼滤波的参数。colorImage为读入的每帧图像

第一帧的时候配置卡尔曼滤波的初始化参数

进入configureKalmanFilter函数，可看到配置了如下参数

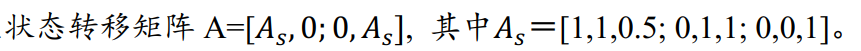
其中Qs为[25, 10, 10]

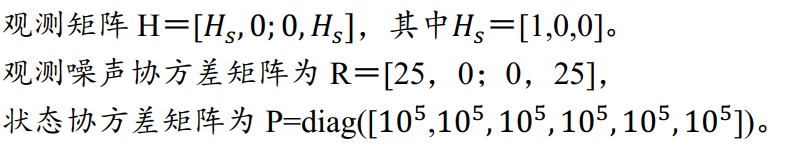
如果已经不是初始位置了，之后的步骤如下：
如果判断检测的位置准确，可以用检测的位置来更新卡尔曼滤波的参数

具体步骤如下：
(1) predict函数得到${\hat{x}}_k^{-}$和$P_k^{-}$
实际观测值为$z_k$，即检测到的位置
(2) correct函数更新参数

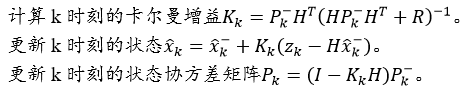
对应的代码中可看到，当检测到目标时，用检测的位置更新参数（predict + correct），没有检测到目标时，就仅更新${\hat{x}}_k^{-}$和$P_k^{-}$（predict）