741. Cherry Pickup（摘樱桃）

You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.

0 means the cell is empty, so you can pass through,
1 means the cell contains a cherry that you can pick up and pass through, or
-1 means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:

Starting at the position (0, 0) and reaching (n - 1, n - 1) by moving right or down through valid path cells (cells with value 0 or 1).
After reaching (n - 1, n - 1), returning to (0, 0) by moving left or up through valid path cells.
When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell 0.
If there is no valid path between (0, 0) and (n - 1, n - 1), then no cherries can be collected.

Example 1:

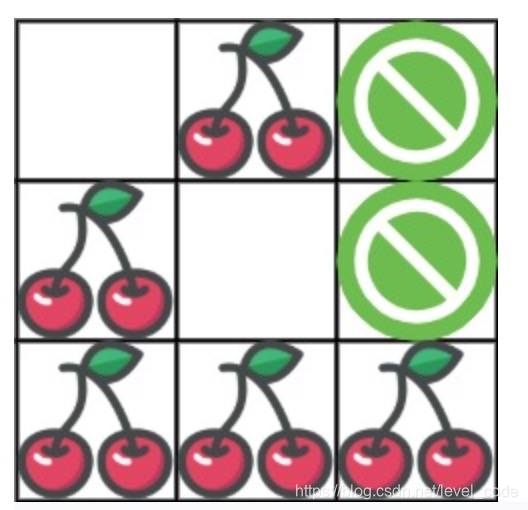
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]]
Output: 5
Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2).
4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]].
Then, the player went left, up, up, left to return home, picking up one more cherry.
The total number of cherries picked up is 5, and this is the maximum possible.

给一个二维grid数组，其中每个位置上的0代表没有樱桃，1代表有一个樱桃，-1代表此路不通。
问从[0][0]走到[n-1][n-1]再从[n-1][n-1]返回[0][0]最多能摘多少个樱桃。
只能向右或向下，返回时只能向左或向上。

思路：
可能会想到用两次 采集最多的DP
但是有个反例，

第一次DP沿中间全是1的路到右下角，再从右下角回去的时候不可能同时采到左右两边的樱桃。

问题转换：
假设两个人从[0][0]出发到[n-1][n-1]，他们走到同一位置的时候只有一个人能摘樱桃。
假设第一个人的坐标是(x1, y1)，只能向右或向下，即x1 + 1或y1 + 1
第二个人坐标(x2, y2)，移动时只能x2 + 1, y2 + 1
即两个人的x，y坐标有一个要+1
起点是一样的， 所以x1 + y1 = x2 + y2，得到y2 = x1 + y1 - x2，可降一维

所以两个人走到一个位置时，他们获得的樱桃数为grid[x1][y1] + grid[x2][y2]（x1,y1不同于x2, y2时加）+ 他们之前位置获得的樱桃数。
两个人的移动方向有4种，其中y2由计算得到：
右， 右 ：y1+1, (y2+1)
右， 下 ：y1+1, x2+1
下， 右 ：x1+1, (y2+1)
下， 下 ：x1+1, x2+1

可得到dp[x1][y1][x2] = grid[x1][y1] + max(dp[x1][y1+1][x2], dp[x1][y1+1][x2+1], dp[x1+1][y1][x2], dp[x1+1][y1][x2+1]) + grid[x2][y2]（x1,y1不同于x2, y2时加）

当两人同时到达[n-1][n-1]时到达终点条件，返回grid[n-1][n-1]

class Solution {
   
   
    int[][]