路面附着系数估计,采用UKF和EKF两种算法。 软件为Matlab/Simulink,非Carsim联合仿真。 dugoff轮胎模块:纯simulink搭非代码 整车模块:7自由度整车模型 估计模块:无迹卡尔曼滤波,扩展卡尔曼滤波,均是simulink现成模块应用无需S-function 带有相关文献和估计说明
在车辆动力学研究领域,准确估计路面附着系数至关重要,它直接关系到车辆的稳定性控制和安全性能。本文将探讨如何在Matlab/Simulink环境下,运用UKF(无迹卡尔曼滤波)和EKF(扩展卡尔曼滤波)两种算法进行路面附着系数估计,且不借助Carsim进行联合仿真。
一、模型构建
1. dugoff轮胎模块
我们采用纯Simulink搭建dugoff轮胎模块。Dugoff模型是一种经典的轮胎模型,它通过考虑轮胎纵向力、侧向力与滑移率之间的关系,来描述轮胎在不同路面条件下的力学特性。虽然没有代码实现,但在Simulink中通过合理设置模块参数与连接关系,能够有效模拟轮胎的工作状态。例如,我们需要设置轮胎的垂直载荷、滚动半径等参数,这些参数将直接影响轮胎力的计算。
2. 整车模块
整车模块选用7自由度整车模型。该模型考虑了车辆的纵向、侧向、垂向运动以及横摆、侧倾、俯仰运动,能较为全面地反映车辆的动力学特性。以下是一个简单的7自由度整车模型在Simulink中的结构示意(非完整代码,仅为示意逻辑):
% 假设车辆质量、转动惯量等参数已定义
m = 1500; % 车辆质量
Iz = 2500; % 横摆转动惯量
% 纵向动力学方程
Fx = Fx1 + Fx2; % 前后轮纵向力之和
ax = Fx / m;
% 横摆动力学方程
Mz = a * Fy1 - b * Fy2; % 横摆力矩
r_dot = Mz / Iz;在这个简化代码中,我们可以看到如何基于车辆参数和轮胎力来计算纵向加速度 ax 和横摆角速度变化率 r_dot。实际在Simulink中,这些方程将通过相应的模块和信号连接来实现。
二、估计模块
1. 无迹卡尔曼滤波(UKF)
UKF是一种基于无迹变换的卡尔曼滤波算法,相比于传统卡尔曼滤波,它能更好地处理非线性系统。在Simulink中,我们直接应用现成的UKF模块。UKF的核心思想是通过选择一组Sigma点来近似状态分布,然后通过这些点的传播来估计状态和协方差。
% UKF初始化
n = 2; % 状态维度
P = [0.1 0; 0 0.1]; % 初始协方差矩阵
x_hat = [0; 0]; % 初始状态估计
% Sigma点计算
lambda = 3 - n;
Wm = [lambda / (n + lambda)];
Wc = [lambda / (n + lambda) + (1 - 1 / (n + lambda))];
for i = 1:n
Wm = [Wm 0.5 / (n + lambda)];
Wc = [Wc 0.5 / (n + lambda)];
end
sigma_points = chol((n + lambda) * P)';
X = [x_hat repmat(x_hat, 1, 2 * n)];
for i = 1:n
X(:, i + n) = x_hat + sigma_points(:, i);
X(:, i) = x_hat - sigma_points(:, i);
end上述代码展示了UKF中Sigma点的计算过程。通过这些Sigma点的传播,我们可以更准确地估计路面附着系数等状态变量。
2. 扩展卡尔曼滤波(EKF)
EKF则是将非线性系统在当前估计点进行线性化,然后应用卡尔曼滤波的框架。同样在Simulink中使用现成模块。在代码层面,EKF的关键在于计算雅克比矩阵。
% EKF线性化(示例)
function [A, H] = linearize(x)
% 假设系统方程和观测方程已定义
% 这里只是示例,实际需根据具体模型推导
A = [1 dt; 0 1]; % 状态转移矩阵近似
H = [1 0]; % 观测矩阵
end在实际应用中,我们需要根据具体的车辆动力学模型和观测方程准确推导雅克比矩阵,以此来实现对路面附着系数的有效估计。
三、相关文献与估计说明
在路面附着系数估计领域,已有许多相关研究。如文献《[文献名称1]》详细探讨了不同滤波算法在路面附着系数估计中的应用,对比了各种算法的优缺点,为我们选择UKF和EKF提供了理论基础。文献《[文献名称2]》则针对7自由度整车模型和dugoff轮胎模块的结合应用进行了深入研究,为模型构建提供了有力参考。
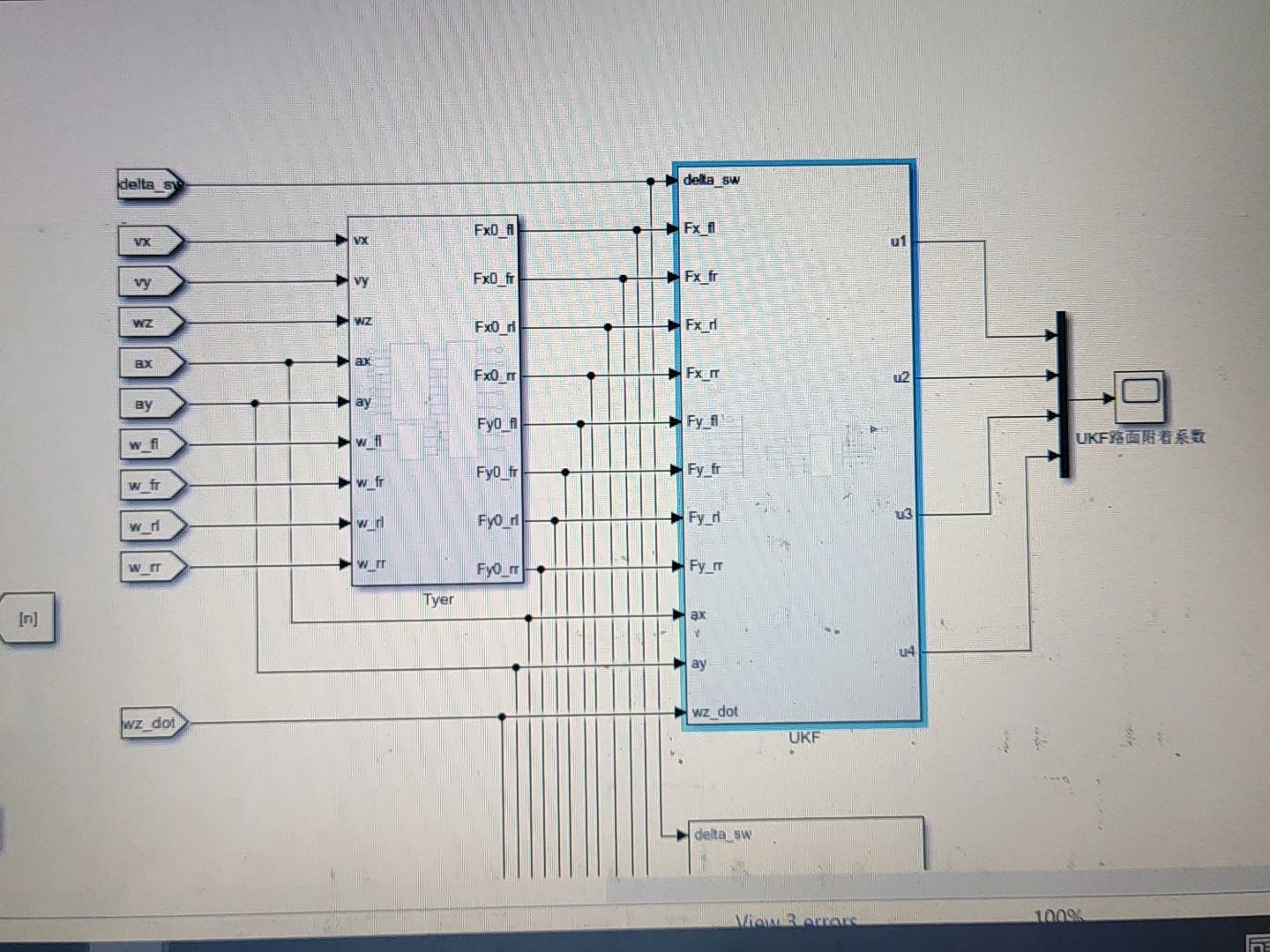
对于UKF和EKF估计路面附着系数,它们各有优势。UKF对非线性系统的处理能力更强,在复杂路况下可能有更好的估计效果;而EKF计算相对简单,在实时性要求较高且非线性程度不是特别强的场景中也能发挥良好作用。通过在Matlab/Simulink中的实践,我们能够直观地对比两种算法在不同工况下对路面附着系数估计的准确性和稳定性,为车辆动力学控制策略的优化提供重要依据。
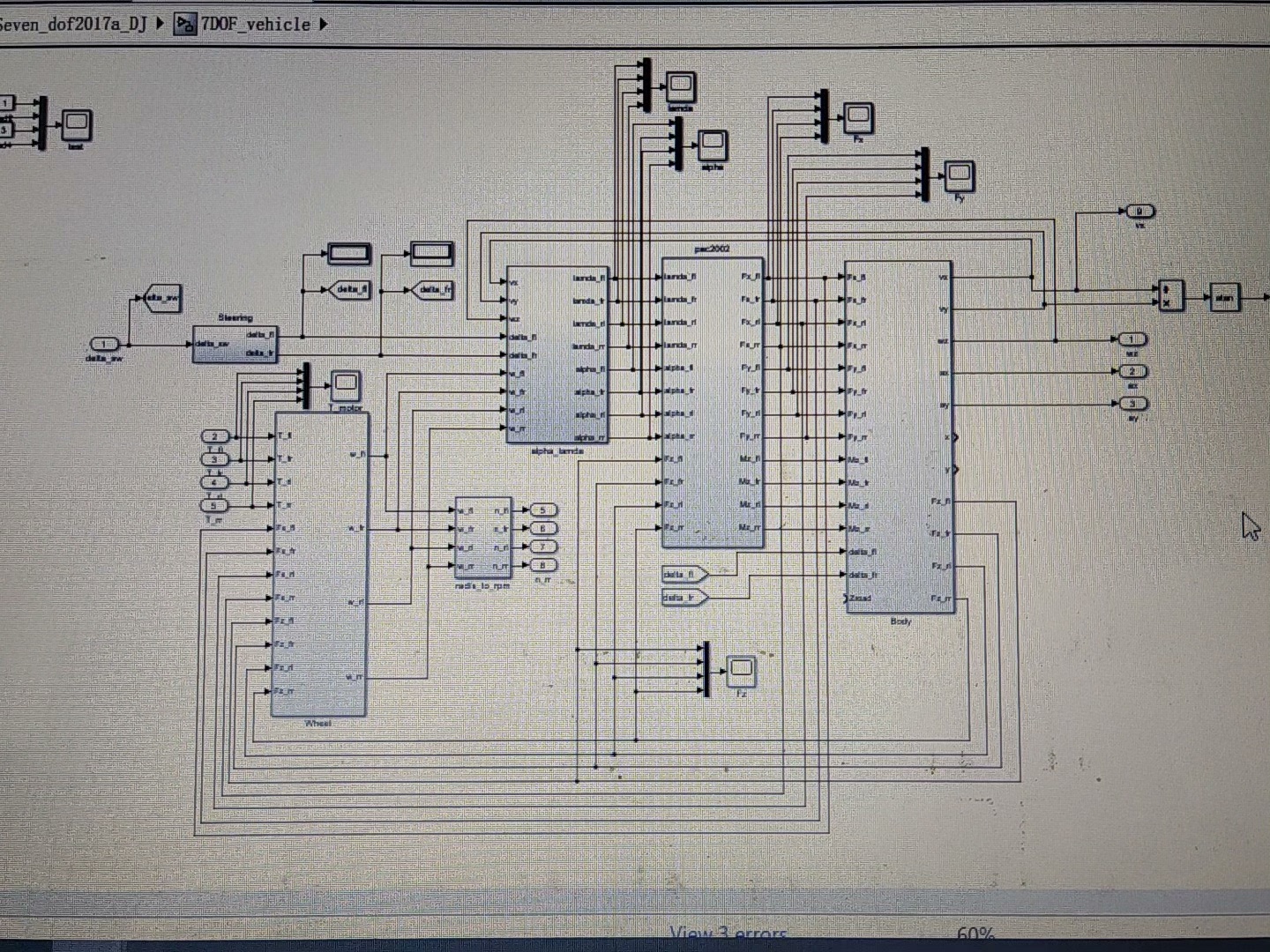
总之,通过Matlab/Simulink搭建的整车和轮胎模型,结合UKF与EKF估计模块,我们实现了一种有效的路面附着系数估计方案,这对于提升车辆主动安全性能具有重要意义。




















 361
361

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








