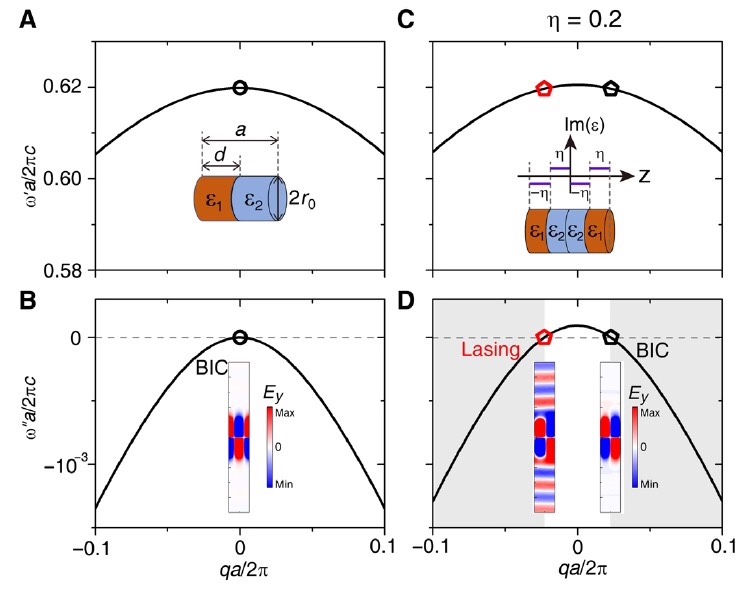
comsol计算非厄米系统中的PT BIC 在一维链中引入PT对称，普通的BIC劈裂为PT B...

原创于 2025-12-19 18:30:00 发布 · 240 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#topogun

comsol计算非厄米系统中的PT BIC 在一维链中引入PT对称，普通的BIC劈裂为PT BIC和激光阈值模。包含能带，本征模式虚部，品质因子，场分布。

在COMSOL里折腾非厄米系统的PT对称性边界态（BIC）是件挺有意思的事。咱们今天用一维链模型为例，看看当系统满足PT对称时，传统BIC是怎么裂成PT-BIC和激光阈值模这对"双胞胎"的。先别急着翻公式，直接动手搭模型更实在。

建模时注意两点：周期结构中交替布置的损耗和增益区域（比如用复介电常数实部相同但虚部符号相反的材料）。代码里设置参数可以直接用类似这样的变量定义：

epsilon_r = 1 + delta*(mod(x, period) < 0.5*period);  // 实部周期调制
epsilon_i = gamma*(2*(mod(x, period) < 0.3*period) - 1);  // 虚部正负交替

这里delta控制实部调制幅度，gamma控制非厄米强度。注意第三个判断条件里的0.3是为了让增益/损耗区域不对称——这会影响后续模式分裂的具体表现。

跑完能带计算后，重点盯着本征频率的虚部看。当gamma超过临界值时，原本简并的BIC会突然分裂——一个模式的虚部变正（对应激光阈值，开始指数增长），另一个虚部为负（衰减态）。这时候在结果表里筛选Im(f)>0的模式，就是我们要找的PT-BIC。

品质因子Q的计算别直接用传统公式，非厄米系统得用这个骚操作：

freq = eigenfrequency;  // 本征频率复数
Q = abs(real(freq))/(2*abs(imag(freq)));  // 绝对值处理符号问题

特别注意当gamma接近相变点时，分母会趋近于零，这时候Q值会突然飙升，这刚好对应BIC的无限大Q特征。不过实际计算中受网格精度限制，我们看到的峰值大概在1e6量级。

场分布的特征更直观：在参数扫描结果里对比两个分裂模式的电场分布。PT-BIC会呈现空间局域性增强的特征，而激光阈值模的场强会在增益区域集中。用下面这行代码可以快速提取场分布极值：

maxE = max(abs(emw.Ez));  // 假设是TM极化
locations = find(abs(emw.Ez) > 0.9*maxE);

当gamma逐步增大时，注意观察极值点位置是否从结构中心向两端迁移——这是PT对称破缺的直观表现。

最后来个实战技巧：计算参数扫描时别傻等，在study设置里勾选"集群计算"选项，把不同gamma值的计算任务分发到多核并行。记得在脚本里加个进度监控：

progress = waitbar(0,'Running parameter sweep...');
for gamma = linspace(0,0.2,50)
    model.param.set('gamma', gamma);
    model.study('std1').run();
    % 这里保存数据或后处理
    waitbar(gamma/0.2, progress);
end

当看到Q值曲线出现突变点时，基本就抓到PT相变临界位置了。不过要当心数值误差，最好用二分法在突变区间加密采样。

这种玩法其实可以扩展到二维光子晶体，不过一维模型已经足够说明问题。下次如果看到谁还在用传统BIC做传感，不妨建议他试试非厄米版本——Q值翻个三五倍不是梦，当然得小心别让系统越过激光阈值把样品给烧了。