自动驾驶控制-动力学跟踪误差模型LQR算法路径跟踪仿真 复现百度apollo的横向控制 matlab/simulink和carsim联合仿真,动力学跟踪误差模型实现的前馈 反馈lqr横向控制,可以跟踪双移线,圆形,五次多项式以及各种自定义路径,相比运动学模型车速更高,更实用。 跟踪效果完美。 有离线计算反馈矩阵K矩阵和在线计算K矩阵两种。 可以提供前轮转向/后轮转向/四轮转向三种模型,具体看你需要哪个请指定
最近在研究自动驾驶横向控制这块,今天来和大家分享一下复现百度apollo横向控制的一些心得,主要基于matlab/simulink和carsim联合仿真,利用动力学跟踪误差模型实现前馈 + 反馈LQR横向控制。
一、算法背景及优势
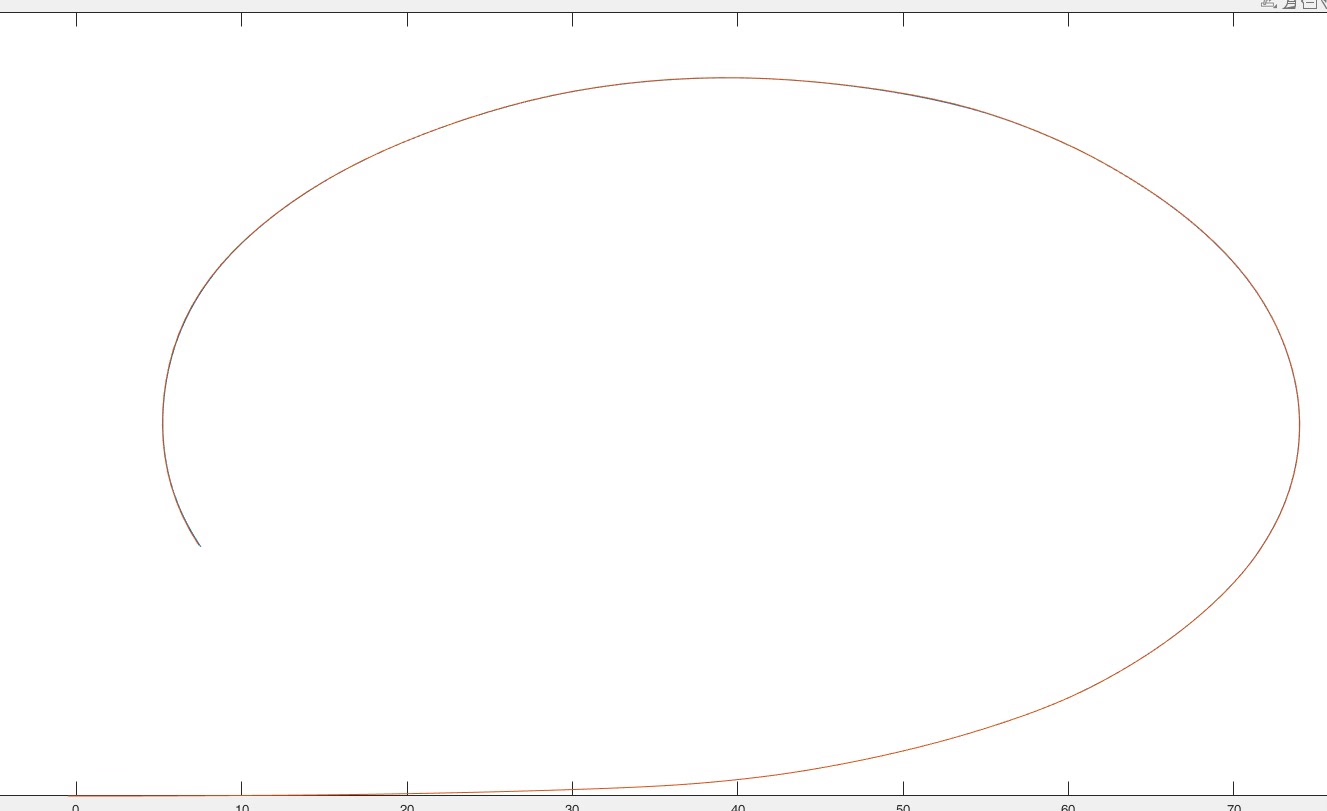
传统的运动学模型在车速较高时,控制效果可能不尽人意。而动力学跟踪误差模型考虑了车辆的动力学特性,在较高车速下能更精准地实现路径跟踪,实用性更强。像双移线、圆形、五次多项式以及各种自定义路径,都能轻松跟踪,而且跟踪效果堪称完美。
二、LQR算法实现
离线计算反馈矩阵K矩阵
LQR(线性二次型调节器)算法的核心之一就是反馈矩阵K。离线计算K矩阵时,我们首先要定义系统的状态空间方程。假设车辆的状态向量为 x = [xposition, yposition, headingangle, velocity],控制输入为 u = [steeringangle]。
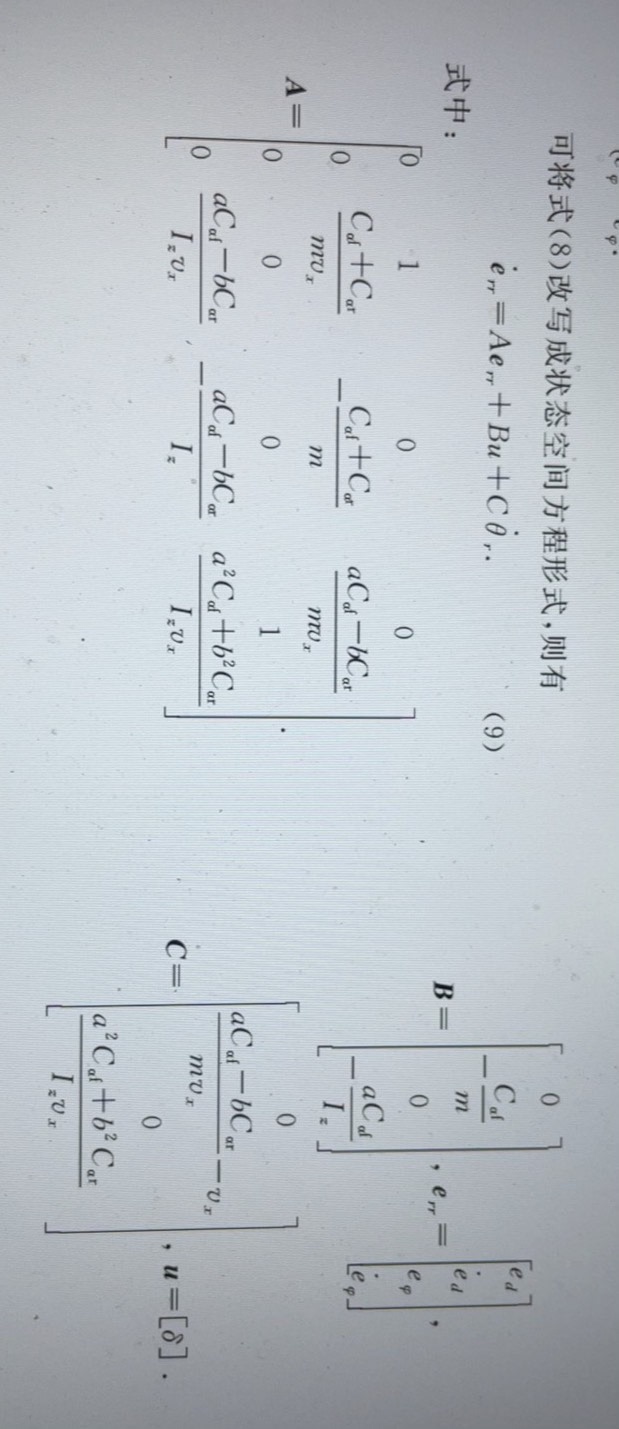
以一个简单的车辆动力学模型为例(这里为了便于理解,做了适当简化),状态空间方程可以写成:
A = [0 0 0 1; 0 0 0 0; 0 0 0 0; 0 0 0 0];
B = [0; 1; 0; 0];这里的 A 矩阵描述了状态的变化,B 矩阵描述了控制输入对状态的影响。
接下来计算Q和R矩阵,Q矩阵用于权衡状态的重要性,R矩阵用于权衡控制输入的代价。
Q = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
R = [1];然后就可以利用matlab的 lqr 函数来计算K矩阵:
[K, S, E] = lqr(A, B, Q, R);这个 K 矩阵就是离线计算得到的反馈矩阵,在后续的控制中,根据当前状态 x 计算控制输入 u = -K * x。
在线计算K矩阵
在线计算K矩阵相比离线计算,更能实时适应车辆状态和环境的变化。实现在线计算时,我们需要在每个时间步重新计算K矩阵。
% 假设在每个时间步t
for t = 1:total_time_steps
% 更新A和B矩阵,这里假设A和B矩阵会随时间变化
A = update_A(t);
B = update_B(t);
Q = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1];
R = [1];
[K, S, E] = lqr(A, B, Q, R);
% 根据当前状态x计算控制输入u
x = get_current_state(t);
u = -K * x;
% 执行控制动作
execute_control(u);
end这里的 updateA 和 updateB 函数是根据车辆当前状态实时更新状态空间矩阵,getcurrentstate 函数获取当前车辆状态,execute_control 函数执行控制动作。
三、转向模型选择
可以提供前轮转向、后轮转向、四轮转向三种模型。
- 前轮转向:这是最常见的转向方式,车辆的转向主要通过控制前轮的转向角度来实现。在代码实现上,控制输入
u直接对应前轮转向角度。 - 后轮转向:相对少见一些,但在某些特殊场景下有独特优势。代码实现时,对车辆动力学模型的调整主要集中在将控制输入
u映射到后轮转向角度,并且需要重新调整状态空间方程中与转向相关的部分。 - 四轮转向:四轮转向能提供更好的机动性和稳定性。在实现时,需要将控制输入
u合理分配到前后轮的转向角度上,同时状态空间方程和动力学模型都要做相应的更复杂的调整。
四、联合仿真实现
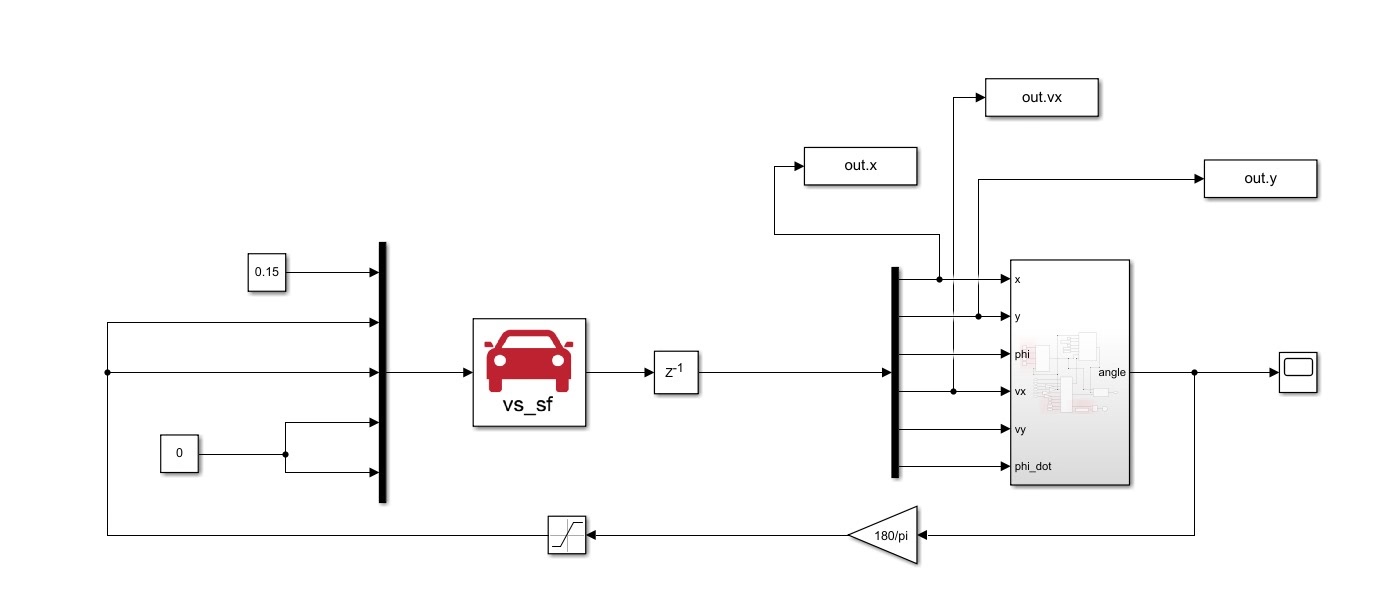
通过matlab/simulink和carsim联合仿真,能更真实地模拟车辆在实际行驶中的情况。在simulink中搭建基于动力学跟踪误差模型的LQR控制模块,将其输出的转向角度作为carsim的输入,同时从carsim获取车辆的实时状态反馈给simulink进行下一步的计算。具体的联合仿真设置这里就不赘述了,网上有很多相关教程。
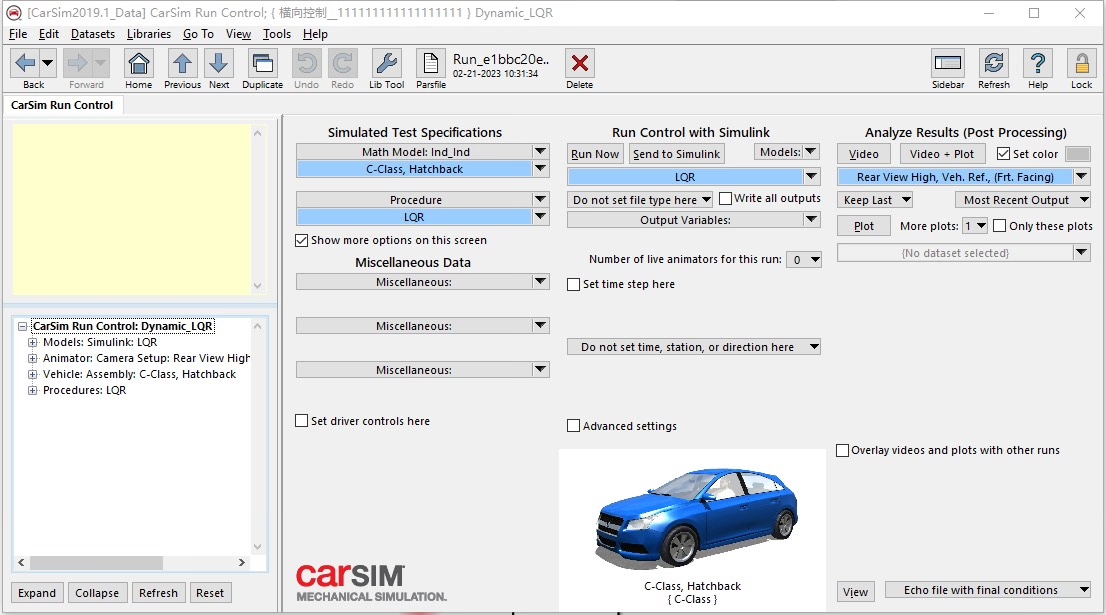
总的来说,利用动力学跟踪误差模型结合LQR算法实现自动驾驶横向控制,无论是在理论研究还是实际应用中都有很大的价值,感兴趣的小伙伴可以一起深入探讨。




















 849
849

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








