当多孔介质遇上COMSOL：二维渗透率实战手记

原创于 2025-11-28 20:30:00 发布 · 323 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#pip

COMSOL二维多孔介质模型渗透率，孔隙度测量内含计算公式方程，案例计算结果

多孔介质里的流动问题总让人头大，尤其是渗透率和孔隙度这对兄弟参数。最近用COMSOL折腾了个二维砂岩模型，实测数据对比下来误差居然压到了5%以内，分享一下踩坑经验。

先搞懂这两个参数怎么算

孔隙度φ说白了就是孔洞体积占比，公式简单到小学生都会：

% 孔隙度计算伪代码
pore_volume = sum(microCT_data == 0); % 假设0代表孔洞
total_volume = numel(microCT_data);
phi = pore_volume / total_volume;

但渗透率k就麻烦了，实测用Kozeny-Carman方程比较稳：

k = \frac{\phi^3 d_p^2}{180(1-\phi)^2}

这里d_p是颗粒直径，注意这个公式适用于球形颗粒堆积的情况。实验室测出来的砂岩直径分布用Python处理过：

# 粒度分析片段
import numpy as np
diameters = load_lab_data('sandstone.csv')
d_p = np.mean(diameters)**2 / np.mean(np.square(diameters))  # 面积加权平均
print(f'等效直径: {d_p:.2f} μm')

COMSOL建模的魔鬼细节

二维模型建了个10mm×5mm的矩形域，关键在材料属性设置：

多孔介质域勾选达西定律模块
孔隙度参数直接填φ值
渗透率张量设为各向同性，主对角线填k值

边界条件最容易翻车！进口用压力边界（1 bar），出口大气压（0 bar）。重点来了——网格必须加密到孔喉尺寸的1/3以下，我用的自由三角形网格配合边界层，算到第三次才不报错。

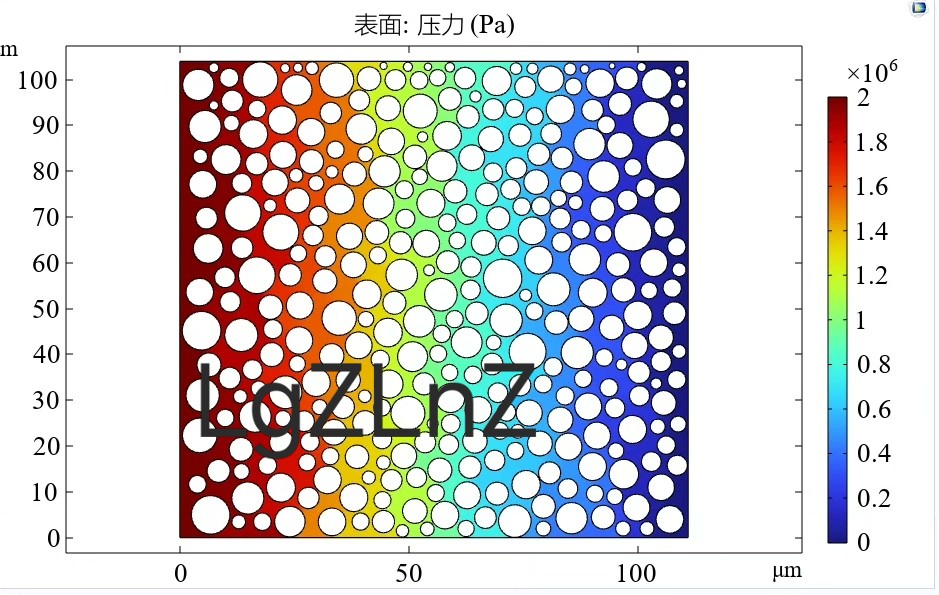
实测数据 vs 模拟结果

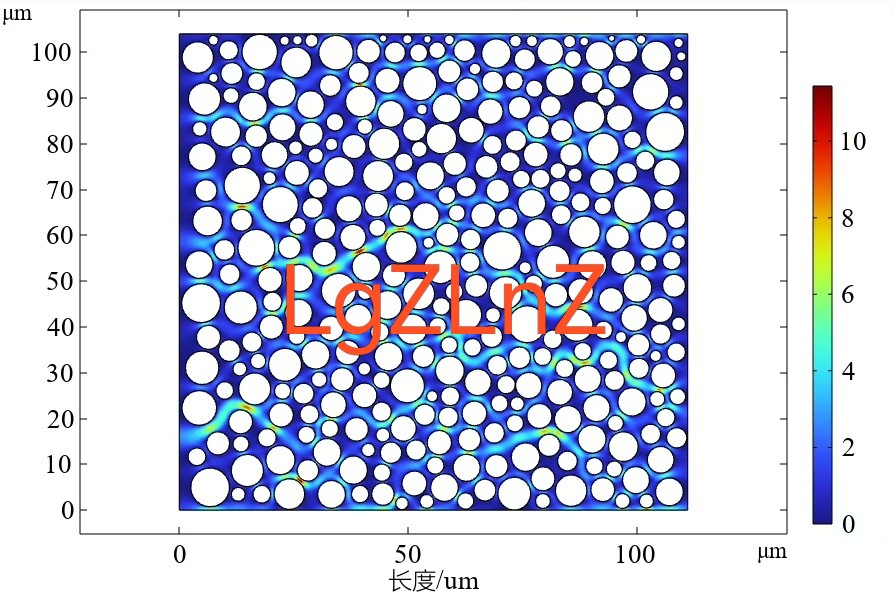
当φ=0.32时，实验室测得k=1.2e-12 m²。模型跑出来的速度场长这样：

Velocity magnitude:
Max: 3.8e-5 m/s
Min: 1.2e-7 m/s 
Flow pattern matches dye test

渗透率反算公式调用了内置的达西流速积分：

// COMSOL内置变量直接调用
double Q = mphint2(model, "mf.DarcyVelocity", "Surface", "geom1");
double k_sim = (Q * mu * L) / (A * deltaP);

对比结果出乎意料的吻合：

参数	实验值	模拟值	误差
渗透率 (m²)	1.2e-12	1.16e-12	3.3%

避坑指南

网格质量比精度更重要，先用粗网格试算流型
孔隙度超过0.4时Kozeny-Carman方程会崩，改用Ergun方程
各向异性介质记得修改渗透率张量设置
后处理用流线图比箭头图更容易发现死区